Algorithme de Savitzky-Golay

Algorithme de Savitzky-Golay appliqué sur un signal gaussien bruité avec un polynôme de degré 3 et une largeur de 9 points. De haut en bas : le signal lissé, la dérivée et la dérivée seconde.

Lissage point par point (mêmes conditions que l'image précédente). L'arc de courbe rouge montre le résultat de la régression sur la fenêtre considérée ; les arcs de courbe en jaune montrent l'extrapolation du polynôme de régression. Les points obtenus pour le lissage sont représentés par des ronds.

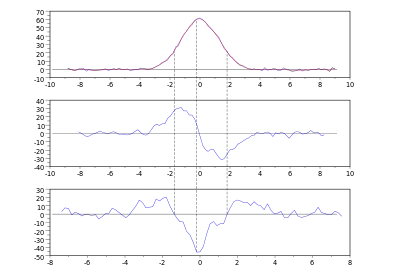
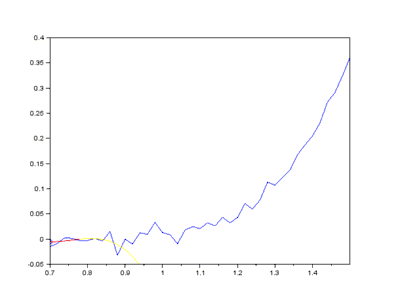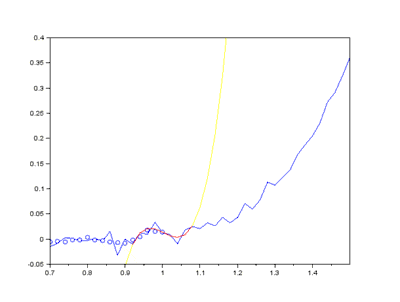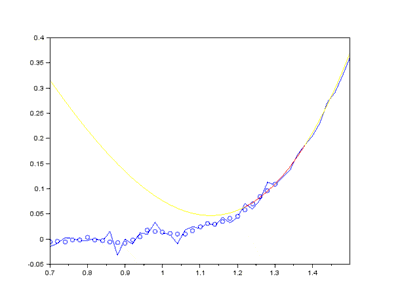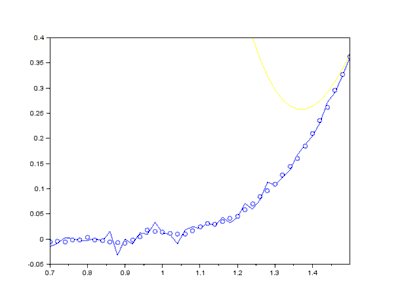
Considérons une courbe y = ƒ(x), et présentant des « aspérités », des oscillations de faibles amplitudes ; on parle de signal bruité. Il s'agit d'une courbe discrète, c'est-à-dire définie par un nuage de points (x(i), y(i))_{1 ≤ i ≤ n}.

L'algorithme de lissage le plus simple est la méthode des moyennes glissantes :

• on considère une fenêtre, un intervalle, de « demi-largeur » ℓ (nombre de points) ;
• on calcule la moyenne y_{ℓ + 1} de la fonction sur l'intervalle [1 ; 2 × ℓ + 1] (l'intervalle a donc une largeur de 2ℓ + 1, ℓ n'est pas exactement la demi-largeur) ;
• on définit un nouveau point (x(ℓ + 1), y_liss(ℓ + 1)) avec y_liss(ℓ + 1) = y_{ℓ + 1} ;
• on fait glisser l'intervalle d'un point et l'on recommence.

Cet algorithme est simple, mais « violent » : il atténue énormément les fortes variations, il écrête les pics.

Pour la suite, nous désignons l'intervalle i comme étant [i – ℓ ; i + ℓ ], l'intervalle de milieu i et de largeur 2ℓ + 1.

Une manière plus fine consiste à considérer un polynôme de degré d, avec d < 2ℓ + 1. Pour chaque intervalle i, on effectue une régression pour déterminer le polynôme P_i minimisant l'erreur au sens des moindres carrés. On définit la valeur lissée

${\displaystyle y_{\textrm {liss}}=P_{i}(x(i)).}$

Par ailleurs, si le polynôme est au moins de degré 1, on peut déterminer la dérivée

${\displaystyle y'_{\textrm {liss}}=P_{i}'(x(i)).}$

et de manière générale, on peut déterminer la d-ième dérivée.

On voit que la méthode des moyennes glissantes est un lissage de Savitzky-Golay avec un polynôme de degré 0.

Illustration du fonctionnement de l'algorithme de Savistky-Golay sur le lissage d'un signal bruité représentant des pics.

Dans la pratique :

• un polynôme de degré 2 permet de prendre en compte la courbure ; un polynôme de degré 3 permet de prendre en compte des points d'inflexion ; il est rarement nécessaire d'aller au-delà ;
• le nombre de points d'un intervalle doit être suffisamment grand devant le degré du polynôme pour que le lissage soit effectif ; s'ils sont égaux, le polynôme passe exactement par tous les points de l'intervalle, il n'y a donc pas de lissage.

On prend donc en général un polynôme de degré 3 et une fenêtre glissante d'au moins 5 points.

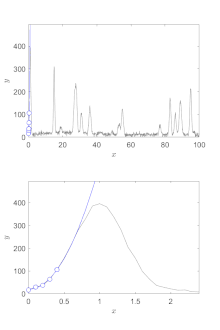
Plus la fenêtre est large, plus la courbe est lissée, mais plus on atténue les variations de petite longueur d'onde. La largeur limite est de l'ordre de la longueur d'onde des détails que l'on veut conserver. Si par exemple on s'intéresse à des pics — cas très fréquents en spectrométrie et en diffractométrie —, on prend en général pour largeur de fenêtre la largeur à mi-hauteur du pic le plus fin.

Concrètement, les coefficients de la régression polynomiale sont calculés par une combinaison linéaire des points de l'intervalle glissant. La valeur lissée, et les valeurs des dérivées, sont donc elles-mêmes des combinaisons linéaires :

${\displaystyle y_{\mathrm {liss} \ i}=b_{0}\cdot y_{i-l}+b_{1}\cdot y_{i-l+1}+\ldots +b_{l}\cdot y_{i}+\ldots +b_{2l}\cdot y_{i+l}=\sum _{k=0}^{2l}b_{k}\cdot y_{i-l+k}}$ ;

${\displaystyle y'_{\mathrm {liss} \ i}=b'_{0}\cdot y_{i-l}+b'_{1}\cdot y_{i-l+1}+\ldots +b'_{l}\cdot y_{i}+\ldots +b'_{2l}\cdot y_{i+l}=\sum _{k=0}^{2l}b'_{k}\cdot y_{i-l+k}}$ ;

…

Si le pas h = x_i – x_{i - 1} est constant[2], les coefficients b_k, b'_k, sont les mêmes partout ; on se retrouve dans le cas d'un filtre à réponse impulsionnelle finie (filtre RIF). On peut donc déterminer au départ les coefficients b_k, b'_k, …, ce qui fournit un algorithme rapide et facile à mettre en œuvre — par exemple avec un tableur ; on parle alors de coefficients de convolution.

Dans ces conditions, on trouve que :

• le lissage est identique que l'on utilise un polynôme de degré 2 (quadratique) ou 3 (cubique) ;
• la dérivation est identique que l'on utilise un polynôme de degré 3 (cubique) ou 4 (« quartique ») ;
• la dérivée seconde est identique que l'on utilise un polynôme de degré 4 (« quartique ») ou 5 (« quintique ») ;
• les coefficients sont symétriques ou anti-symétriques, selon l'ordre de dérivation :

b_k = b_{2ℓ – k} ; b'_k = –b'_{2ℓ – k} ; …

• on a toujours b'_l = 0 : le point x_i ne contribue pas au calcul de y'_{liss i}.

Les valeurs des coefficients sont tabulées pour des tailles de fenêtre (intervalle glissant) données. Par exemple, pour une fenêtre de 5 points et un polynôme de degré 3 :

${\displaystyle y_{\mathrm {liss} \ i}={\frac {1}{35}}(-3\cdot y_{i-2}+12\cdot y_{i-1}+17\cdot y_{i}+12\cdot y_{i+1}-3\cdot y_{i+2})}$ ;

${\displaystyle y'_{\mathrm {liss} \ i}={\frac {1}{12h}}(1\cdot y_{i-2}-8\cdot y_{i-1}+0\cdot y_{i}+8\cdot y_{i+1}-1\cdot y_{i+2})}$ ;

${\displaystyle y_{\mathrm {liss} \ i}^{\prime \prime }={\frac {1}{7h^{2}}}(2\cdot y_{i-2}-1\cdot y_{i-1}-2\cdot y_{i}-1\cdot y_{i+1}+2\cdot y_{i+2})}$.

Les tableaux ci-dessous donnent les coefficients de convolution pour des degrés de polynôme et des largeurs de fenêtre données.

Remarque : la normalisation utilise le pas d'échantillonnage h.

On se place en un point k donné. Les coordonnées du point expérimental sont (x_k, y_k).

Pour déterminer les coefficients de corrélation, on effectue un changement de variable afin d'avoir une abscisse centrée réduite — c'est-à-dire que l'intervalle sur lequel on effectue la régression devient [–ℓ ; ℓ ] : on pose

${\displaystyle z={\frac {x-{\bar {x}}}{h}}}$

où

• x est la moyenne des valeurs de x sur l'intervalle [x_{k – ℓ} ; x_{k + ℓ}] considéré, c'est le centre de la fenêtre ;
• h est le pas d'échantillonnage (distance entre deux points voisins).

L'abscisse z prend les valeurs (–ℓ ; –ℓ + 1 ; … ; –1 ; 0 ; 1 ; … ℓ ). Par exemple, pour une fenêtre glissante de 5 points, on a (z_i)_{1 ≤ i ≤ 5} = (–2 ; –1 ; 0 ; 1 ; 2).

Le polynôme de degré d s'exprime alors sous la forme :

${\displaystyle y=P(z)=a_{0}+a_{1}\cdot z+a_{2}\cdot z^{2}+\ldots +a_{d}\cdot z^{d}}$

Considérons la fonction vectorielle

${\displaystyle \mathrm {F}$ :{\begin{pmatrix}a_{1}\\a_{2}\\\vdots \\a_{d}\end{pmatrix}}\longmapsto {\begin{pmatrix}\mathrm {P} (z_{1})\\\mathrm {P} (z_{2})\\\vdots \\P(z_{2l+1})\end{pmatrix}}}

avec

${\displaystyle {\begin{pmatrix}P(z_{1})\\P(z_{2})\\\vdots \\P(z_{2l+1})\end{pmatrix}}\simeq {\begin{pmatrix}y_{k-l}\\y_{k-l+1}\\\vdots \\y_{k+l}\end{pmatrix}}}$

Sa matrice jacobienne s'écrit

${\displaystyle \mathrm {J} =\left({\frac {\partial P}{\partial a_{j}}}(z_{i})\right)={\begin{pmatrix}1&z_{1}&z_{1}^{2}&\cdots &z_{1}^{d}\\1&z_{2}&z_{2}^{2}&\cdots &z_{2}^{d}\\\vdots &\vdots &\vdots &&\vdots \\1&z_{2l+1}&z_{2l+1}^{2}&\cdots &z_{2l+1}^{d}\end{pmatrix}}}$

La solution des équations normales

${\displaystyle {}^{\mathrm {t} }\mathrm {J} \mathrm {J} (a_{i})={}^{\mathrm {t} }\mathrm {J} (y_{j})}$

est donc

${\displaystyle (a_{i})=\left({}^{\mathrm {t} }\mathrm {J} \mathrm {J} \right)^{-1}{}^{\mathrm {t} }\mathrm {J} (y_{j})}$

La valeur de la courbe lissée est la valeur du polynôme au centre de l'intervalle :

${\displaystyle y_{\textrm {liss}}=P(0)=a_{0}}$ ;

Pour les dérivées successives :

${\displaystyle y'_{\mathrm {liss} }={\frac {\partial P}{\partial x}}(x_{k})={\frac {\partial z}{\partial x}}(0){\frac {\partial P}{\partial z}}(0)={\frac {1}{h}}a_{1}}$ ;

${\displaystyle y_{\mathrm {liss} }^{\prime \prime }={\frac {\partial ^{2}\mathrm {P} }{\partial x^{2}}}(x_{k})={\frac {\partial ^{2}z}{\partial x^{2}}}(0){\frac {\partial \mathrm {P} }{\partial z}}(0)+{\frac {\partial z}{\partial x}}{\frac {\partial ^{2}\mathrm {P} }{\partial z^{2}}}(0)={\frac {2}{h^{2}}}a_{2}}$.

Par exemple, pour un polynôme de degré d = 3 et une fenêtre de 5 points, donc ℓ = 2 :

${\displaystyle \mathrm {J} ={\begin{pmatrix}1&-2&4&-8\\1&-1&1&-1\\1&0&0&0\\1&1&1&1\\1&2&4&8\end{pmatrix}}{\text{$ ; }}{}^{\mathrm {t} }\mathrm {J} ={\begin{pmatrix}1&1&1&1&1\\-2&-1&0&1&2\\4&1&0&1&4\\-8&-1&0&1&8\end{pmatrix}}}

${\displaystyle {\begin{pmatrix}a_{0}\\a_{1}\\a_{2}\\a_{3}\end{pmatrix}}=\left({}^{\mathrm {t} }\mathrm {J} \mathrm {J} \right)^{-1}{}^{\mathrm {t} }\mathrm {J} {\begin{pmatrix}y_{k-2}\\y_{k-1}\\y_{k}\\y_{k+1}\\y_{k+2}\end{pmatrix}}={\begin{pmatrix}-3/35&12/35&17/35&12/35&-3/35\\1/12&-8/12&0&8/12&-1/12\\2/14&-1/14&-2/14&-1/14&2/14\\-1/12&2/12&0&-2/12&1/12\end{pmatrix}}{\begin{pmatrix}y_{k-2}\\y_{k-1}\\y_{k}\\y_{k+1}\\y_{k+2}\end{pmatrix}}}$.

On a donc :

${\displaystyle y_{\mathrm {liss} \ k}=a_{0}={\frac {1}{35}}(-3y_{k-2}+12y_{k-1}+17y_{k}+12y_{k+1}-3y_{k+2})}$ ;

${\displaystyle y'_{\mathrm {liss} \ k}={\frac {a_{1}}{h}}={\frac {1}{12h}}(y_{k-2}-8y_{k-1}+0y_{k}+8_{k+1}-y_{k+2})}$ ;

${\displaystyle y_{\mathrm {liss} \ k}^{\prime \prime }={\frac {2}{h^{2}}}a_{2}={\frac {1}{7h^{2}}}(2y_{k-2}-y_{k-1}-2y_{k}-y_{k+1}+2y_{k+2})}$.