Convection mantellique
La convection mantellique est un phénomène physique se produisant à l’intérieur du manteau terrestre. Il peut avoir lieu sur d'autres planètes ou satellites telluriques sous certaines conditions. La convection mantellique est une composante essentielle de la théorie de la tectonique des plaques.
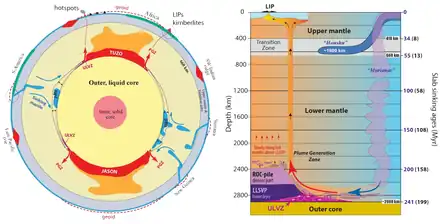
Il existe une différence notable de température entre le manteau lithosphérique et l'asthénosphère sous-jacente, qui est responsable d'une descente de manteau froid lithosphétique (au niveau des zones de subduction) dans l'asthénosphère plus dense[1]. Une remontée plus anecdotique de matériel mantellique profond chaud est observée au niveau des points chauds. Ces deux mécanismes sont autorisés par le comportement ductile des roches à grande échelle, qui permet au réseau cristallin de se déformer sans se briser (fluage plastique).
Le nombre de Rayleigh Ra, sans dimension, exprime le rapport des forces impliquées dans la convection, qui débute si Ra dépasse une valeur critique, caractéristique d'un milieu donné. Le calcul du nombre de Rayleigh pour le manteau montre une possibilité de convection, en accord avec les observations.
Estimation du nombre de Rayleigh
Le calcul du nombre de Rayleigh permet d’affirmer que le manteau est effectivement en convection. La difficulté réside dans la détermination des paramètres intervenant dans la formule de Ra. La valeur calculée couramment est de Ra = 5 × 108, dépassant de loin le nombre de Rayleigh critique Rac proche de 1 000, ce qui témoigne de l’existence réelle d’une convection mantellique dynamique mais lente.
Estimation du coefficient d'expansion thermique et de la diffusivité thermique
Ils sont obtenus à l’aide d’expériences de géophysique réalisées en laboratoire sur les minéraux constitutifs du manteau (olivine, pyroxènes), trouvés dans des roches mantelliques exhumées par tectonique ou par le volcanisme. Ces expériences thermodynamiques sont faites à haute pression et haute température pour simuler les conditions du manteau.
Expérimentalement on trouve des valeurs de l'ordre de :
- capacité thermique massique : 103 J/kg K ;
- masse volumique : 3 × 103 kg/m3 ;
- coefficient d'expansion thermique : 3 × 10−5 K−1 ;
- conductivité thermique : 3 W m−1 K−1.
L’estimation de ces paramètres permet de calculer la diffusivité thermique : 10−6 m2/s.
Estimation de ΔT
ΔT est la différence de température entre la base (2 885 km) et la surface du manteau (30 km), soit une profondeur de l'ordre de 2 900 km. Ce paramètre est difficile à estimer car il est impossible d’effectuer des mesures directes, mais il est possible de l’estimer par le flux de chaleur du manteau.
Si l’on ne considère une Terre sans convection, la température du manteau est due à plusieurs phénomènes :
- la désintégration d’éléments radioactifs naturels contenus dans les minéraux mantelliques comme l’uranium (U), le thorium (Th) et le potassium (K). Les quantités estimées pour ces éléments sont 24 ppm pour K, 0,006 ppm pour U et 0,002 ppb pour Th. Le flux de chaleur H produit par unité de masse avoisine 5 × 10−12 W/kg. Ce flux de chaleur était bien plus important dans la jeunesse de la Terre, du fait de la diminution progressive des teneurs en éléments radioactifs instables avec le temps et leur désintégration ;
- la libération de chaleur initiale de la Terre lors de son accrétion.
Si la chaleur était uniquement transférée par conduction dans le manteau, l’estimation de ΔT serait proche de 21 000 K. Les études expérimentales montrent qu'une telle température ne permettrait pas l'état solide du manteau jusqu'à sa base.
La température terrestre à 660 km de profondeur peut être estimée à l’aide des transitions de phase de l’olivine. L’olivine α subit diverses transformations avec la profondeur qui témoignent de conditions précises de température et de pression. Ces transitions sont décelables en profondeur par l’étude des ondes sismiques, dont la vitesse change au niveau de ces transitions. À la limite manteau supérieur – manteau inférieur, l’olivine γ se transforme en pérovskite + magnésiowüstite, ce qui correspond d’après le diagramme de phase de l’olivine à une température de 1 830 K.
On ne connaît pas la température de la transition manteau inférieur – noyau externe, mais un ordre de grandeur peut être obtenu par déduction : en profondeur, le fer cristallise à la limite graine – noyau externe à une température de 5 000 K, ce qui signifie que la température de la base du manteau est comprise entre 2 000 K et 5 000 K.
Note : si on considère que la Terre est en convection idéale (adiabatique), on peut calculer en toute profondeur la température grâce au gradient adiabatique, mais cette partie cherche à estimer le nombre de Rayleigh du manteau pour savoir s’il y a convection ou non.
Estimation de la viscosité ν
On peut estimer la viscosité d’une roche mantellique en laboratoire, mais les conditions thermodynamiques du manteau sont très difficiles à obtenir en laboratoire.
Elle est aussi possible par l’étude des remontées isostatiques post-glaciaires, qui renseigne sur la valeur de la viscosité de l’asthénosphère. Lors d’une glaciation, le poids d’une calotte glaciaire sur un continent crée une dépression dans la lithosphère sous-jacente, du fait du principe d’isostasie. Après la fonte de la glace, qui est un évènement très rapide, la lithosphère n’est plus soumise à ce poids et remonte par rebond isostatique. La vitesse de la remontée dépend directement de la viscosité de l’asthénosphère et de la lithosphère. Les données historiques, des mesures de nivellement etc. permettent de retracer l’historique du rebond, et par application aux équations de la mécanique des fluides, il est possible de déterminer la viscosité.
La viscosité dynamique η est estimée à environ 1021 Pa s, ce qui donne une viscosité de 3 × 1017 m2 s−1, en accord avec les études théoriques de la déformation de l’olivine à haute température.
Le nombre calculé est très élevé en comparaison avec un fluide « classique » gazeux ou liquide : le manteau en convection est à l’état solide et déformable.
Modèle de la convection
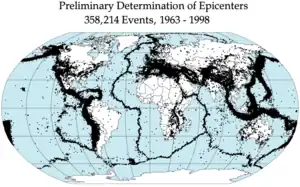
Les hypothèses faites pour l’étude de la convection mantellique sont les suivantes : il s’agit d’un système convectif dont la viscosité dépend fortement de la température, possédant deux couches limites dans le cas d’une surface « libre », où la couche limite supérieure très visqueuse se découpe en plaques, générant une faible déformation intraplaque et beaucoup de déformation interplaque, comme le montre la carte de répartition des séismes sur la surface du globe terrestre. Les zones de subduction où du matériel froid et dense plonge en profondeur constitue le flux descendant, alors que les dorsales océaniques constituent le flux ascendant.
Du fait du nombre de Rayleigh très grand (Ra = 108), on estime que la convection possède une structure chaotique, à savoir que les mouvements ascendants et descendants ne se situent pas aux mêmes endroits avec le temps, mais ceci ne s’observe pas en pratique : les plaques seraient parsemées de volcans, les panaches chauds pouvant remonter en n’importe quel endroit, alors que l’on sait que les points chauds sont relativement immobiles. L’étude des flux de chaleur montre que l’énergie évacuée par le manteau sort principalement au niveau des dorsales (100 mW/m2 en moyenne), et beaucoup moins au niveau des plaques lithosphériques plutôt isolantes (12 mW/m2 en moyenne). Les remontées de panaches s’accumuleraient sous la lithosphère océanique (par exemple la plaque pacifique pour la chaîne Hawaii – Empereur) ou bien continentale (cas des trapps). Si une trop forte accumulation de matériel se fait sous un continent, la lithosphère continentale va s’amincir dans le cadre d’un rifting pour donner naissance à un nouvel océan, c’est ce que l’on suppose dans la région actuelle de l'Afar.
Couche limite supérieure
Dans tous les modèles de convection, on considère que la couche limite supérieure du système est constituée par la lithosphère océanique rigide, « flottant » sur l’asthénosphère moins visqueuse et plus dense. Ceci est confirmé théoriquement par l’étude du profil de température et du flux de chaleur au niveau de la croûte océanique, qui suivent les lois physiques de la convection, à savoir une augmentation très rapide de la température moyenne dans les premières dizaines de kilomètres de profondeur, c'est-à-dire que la couche limite supérieure fixe une grande partie de la différence de température du système convectif. Ceci est confirmé par la différence de température de plus de 1 000 K existant entre les roches à la dorsale et celles qui constituent le plancher océanique - qui s'en éloignent symétriquement.
Centre de la cellule
Conformément aux modèles, la variation de température est relativement faible vis-à-vis de la profondeur. On l’estime de l’ordre de quelques centaines de degrés.
La tomographie sismique permet de mettre en évidence des hétérogénéités de température dans le manteau, dues aux mouvements ascendants (panaches) et descendants (croûte océanique subductée).
Couche limite inférieure
Selon les modèles, elle est placée soit a 660 km de profondeur, à la limite manteau supérieur – manteau inférieur, soit à la limite manteau – noyau à 2 900 km de profondeur, jusqu’à une couche hypothétique nommée d″.
Modèles de la convection mantellique

Plusieurs modèles ont été imaginés pour rendre compte de la structure des cellules de convections du manteau.
Modèle à une couche
Dans ce modèle, la lithosphère continentale subduite plonge en profondeur jusqu’à la couche limite inférieure étant ici l’interface manteau – noyau. Ce matériel peut se transformer en un panache ascendant moins visqueux que les roches l’entourant et remontant en surface par les volcans de points chauds. Les mouvements ascendants et descendants décrivent des cellules de convection. Du matériel peut ressortir au niveau des dorsales océaniques de façon passive. Il n’y a qu’un type de cellule de convection brassant l’ensemble de l’épaisseur du manteau : ce modèle est dit « à une couche ».
Modèle à deux couches
Contrairement au modèle précédent, on imagine dans le modèle « à deux couches » qu’il existe des cellules de convection dans le manteau inférieur générées par les panaches ascendants, et d’autres à l’intérieur du manteau supérieur, permettant la sortie de matériel au niveau des dorsales océaniques, du fait de la discontinuité de phases de l’olivine à 660 km de profondeur.
Modèle actuellement accepté
Le modèle le plus vraisemblable est un modèle intermédiaire entre les deux précédents, plus en accord avec les observations tomographiques que ceux-ci. La croûte océanique subduite peut descendre jusqu’à la couche d″ et être à l’origine de panaches ascendants, ou bien glisser le long de l’interface manteau supérieur – manteau inférieur, et générer aussi des panaches. Les cellules de convection se limitent au manteau inférieur. Du matériel peut sortir passivement au niveau des dorsales en extension, qui ne sont pas enracinées en profondeur.
Références
- http://planet-terre.ens-lyon.fr/article/convection-mantellique-tectonique-plaques.xml
- (en) M. Kronbichler, T. Heister et W. Bangerth, « High accuracy mantle convection simulation through modern numerical methods », Geophysical Journal International (en), vol. 191, no 1, , p. 12-29 (DOI 10.1111/j.1365-246X.2012.05609.x, lire en ligne).
Voir aussi
Bibliographie
- Géodynamique, L. Jolivet et H.-C. Nataf, ed. Dunod, 1998, 226 p.
- Dossier de conférence du 01 - 04 - 2005 : La convection mantellique, mythes, réalités et questions par Pierre Thomas, 100 diapositives.
- La géochimie, Francis Albarède, Gordon & Breach, 2001




