Capture électronique
La capture électronique (plus précisément capture électronique orbitale, cf. section « Notations »), ou désintégration ε, ou parfois désintégration bêta inverse, est un processus de physique nucléaire au cours duquel un noyau atomique déficient en neutrons absorbe un électron situé sur une couche électronique de l’atome. Variante de la désintégration β+, sa description théorique est formulée par la théorie publiée par Enrico Fermi en 1933. La conséquence de la capture, selon la loi de conservation de la charge électrique, est qu’il y a une transmutation de l’atome puisqu’un proton, en absorbant l’électron intrus devient un neutron, et émission d’un neutrino électronique pour conserver le nombre leptonique ; l’atome qui avait Z protons et N neutrons devient un atome avec (Z-1) protons et (N+1) neutrons :
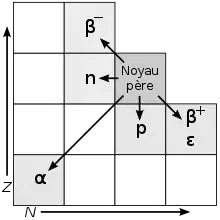
où X et Y désignent respectivement le noyau père et le noyau fils. A est le nombre de masse.
Ce processus nucléaire est suivi de plusieurs émissions de photons pour que l’atome atteigne son état fondamental. D’une part, le noyau nouvellement formé peut se désexciter en émettant des photons γ s’il avait été formé dans un état excité. D’autre part, le cortège électronique se réorganise afin de combler la lacune laissée dans les couches internes par l’électron capturé. Cette réorganisation est accompagnée d’émissions de rayons X et/ou d’électrons Auger.
Historique


Irène et Frédéric Joliot-Curie sont les premiers, en , à proposer la possibilité pour un noyau de décroitre après absorption d’un électron. Ils écrivent ainsi dans le Journal de Physique et Le Radium « On peut encore supposer que l’isotope inconnu Na22 n’est pas stable et se transforme spontanément en Ne22 par captation d’un électron extranucléaire[1]. » Il a par la suite été montré que le sodium 22 décroit effectivement par capture électronique à hauteur d’environ 10 %[2].
La capture électronique a été théorisée pour la première fois par Gian-Carlo Wick dans un papier publié en italien le [3] - [4]. Dans ce papier, Wick applique la récente théorie de la désintégration bêta proposée par Enrico Fermi et présente une autre désintégration possible en plus de la radioactivité β+ dont la découverte avait été annoncée six semaines auparavant, le , par Irène Curie et Frédéric Joliot devant l’Académie des Sciences[5]. Il calcule la probabilité de se désintégrer par émission de positron et par capture électronique. Du fait de la découverte de la radioactivité β+ par le couple Joliot-Curie, Emilio Segrè écrit qu’il existe un petit doute concernant le fait de savoir si Wick a vraiment été le premier à mentionner la capture d’électrons K et à calculer sa probabilité[4] même si les Joliot-Curie ne font pas référence à la capture électronique dans leur rapport de 1934. La possibilité de la capture électronique a aussi été envisagée par Hans Bethe et Rudolf Peierls deux mois après le papier de Wick[6]. Par la suite, le calcul de Wick a été repris et amélioré par Hideki Yukawa et Shōichi Sakata[7].
La capture électronique d’électron K a été observée pour la première fois par Luis Alvarez dans la décroissance du vanadium 48. Il a décrit son expérience dans un papier de Physical Review publié en 1937[4] - [8] - [9]. Le vanadium 48 a été produit par bombardement de titane par des deutérons, tandis que la détection des photons X caractéristiques du titane a été faite à l’aide d’une feuille d’aluminium. La période de trois ans séparant la prédiction théorique de l’observation expérimentale s’explique du fait de la difficulté de mesurer le photon X ou l’électron Auger qui résulte du réarrangement atomique qui suit la capture électronique. Par la suite, Alvarez a continué à étudier la capture électronique dans le gallium 67[10] ainsi que d’autres nucléides[4] - [11]. Quelques années plus tard, D. H. W. Kirkwood, Bruno Pontecorvo et Geoffrey Chalmers Hanna en 1948[12], puis en 1949[13] ont observé la capture électronique d’électron L dans la décroissance de l’argon 37. Puis, P. W. Dougan a mesuré, au cours de sa thèse de doctorat, la capture d’électron M en 1961 dans la décroissance du germanium 71[14].
Point de vue fondamental
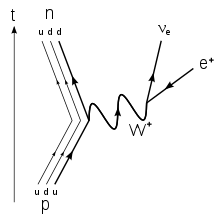
Le proton et le neutron n’étant pas des particules élémentaires, le processus de la capture électronique implique, au niveau fondamental, les quarks up et down qui composent les protons et les neutrons. La théorie électrofaible prévoit qu’un boson W+ soit échangé entre le quark up et l’électron transformant le quark up en quark down et l’électron en neutrino électronique.
Aspects énergétiques
Valeur Q
La valeur Q exprime la quantité d’énergie relâchée par une réaction. Dans le cas d’une réaction de capture électronique, elle vaut
où et sont respectivement les énergies de masse du noyau père (avant la désintégration) et du noyau fils (après la désintégration), l’énergie d’excitation du noyau père (égale à 0 MeV sauf dans le cas d’isomères), est l’énergie de liaison de l’électron qui a participé au processus et correspond à la différence d’énergie entre les orbitales atomiques du noyau père () et du noyau fils (). Ce dernier terme est généralement négligé sauf dans le cas d’atomes lourds (avec un grand numéro atomique Z) où cette valeur peut atteindre environ 10 keV[15]. En revanche, peut atteindre la centaine de keV dans les noyaux les plus lourds, comme dans le bismuth 208[16], et n’est généralement pas négligé[17].
Compte tenu du fait qu’une réaction ne peut avoir lieu que lorsque la valeur Q est positive (de l’énergie est relâchée par le système), la capture électronique n’a lieu que lorsque
En pratique, et sont souvent négligeables par rapport à la différence de masses des noyaux père et fils (d’autant plus si on considère les électrons des couches L, M, N, …) ce qui revient à dire que la capture électronique se produit dès que le noyau fils est moins massif que le noyau père. Néanmoins, la présence de ce seuil permet, par exemple, d’expliquer pourquoi la décroissance par capture électronique de l’américium 244 dans son état fondamental n’a pas été observée tandis que ce mode de désintégration a été observée, bien qu’avec une faible probabilité, dans son isomère à 86,1 keV. En effet, la différence de masse entre l’²⁴⁴Am et le ²⁴⁴Pu est d’environ 75 keV/c2 tandis que l’énergie de liaison des électrons de la couche K est de l’ordre de 140 keV. Ainsi la désintégration par capture électronique de l’²⁴⁴Am n’est-elle possible que par capture d’un électron de couches supérieures (L, M, N, …) ce qui est beaucoup moins probable[Note 1] que la capture d’un électron de la couche K. En revanche, dans l’isomère ²⁴⁴ᵐAm, la capture d’électron de la couche K est possible puisqu’il faut prendre en compte l’énergie du niveau excité. On a ainsi une énergie « disponible » de 164 ± 9 keV[19] ce qui est supérieure aux 140 keV correspondant à l’énergie de liaison d’un électron de la couche K. La probabilité étant plus importante, ce mode de décroissance a pu être observé à hauteur de 0,036 ± 0,001 %[19].
Neutrino
Après une capture électronique, deux corps peuvent se partager l’énergie : le noyau de recul et le neutrino électronique. Cela se traduit par le fait que ces deux particules ont une énergie cinétique bien définie contrairement au cas de la désintégration bêta où le spectre en énergie est continu du fait de la présence d’une troisième particule (la particule bêta). L’énergie du neutrino dépend donc uniquement de l’énergie disponible. Comme indiqué dans la section précédente, cette énergie dépend principalement de la masse des noyaux père et fils et de l’énergie de liaison de la couche électronique sur laquelle se trouve l’électron participant à la capture électronique. Ainsi, pour un noyau père donné, le neutrino peut-il prendre plusieurs énergies différentes suivant les différentes couches électroniques impliquées (K, L, M, …).
En tenant compte de la conservation de l’énergie et de la quantité de mouvement, en négligeant les effets relativistes et en considérant le neutrino sans masse, on démontre que l’énergie cinétique du neutrino s’exprime à l’aide de la relation suivante
D’après la conservation de l’énergie, on peut écrire
où est la valeur Q donnée dans la section précédente, et sont respectivement les énergies cinétiques du neutrino et du noyau de recul. Le noyau père étant au repos au moment de la désintégration (sa quantité de mouvement est nulle), on peut écrire , d’après la conservation de la quantité de mouvement.
En exprimant l’énergie cinétique du noyau de recul sous sa forme classique puis en remplaçant par , on obtient
Par ailleurs, le neutrino étant considéré comme sans masse, sa quantité de mouvement s’exprime par la relation . Ainsi, en ajoutant au numérateur et au dénominateur, obtient-on
Il s’agit alors de résoudre cette équation du second degré. On réécrit l’équation sous la forme
avec , et . Le discriminant est égal à
Les deux solutions sont alors
Parmi les deux solutions mathématiquement exactes, seule la solution avec le signe « + » est correcte physiquement étant donné que celle avec le signe « - » donne une énergie cinétique négative. Finalement, l’énergie cinétique du neutrino est donc égale à
De ce résultat, il est possible de voir que le neutrino emporte quasiment l’ensemble de l’énergie disponible. En effet, le rapport est proche de 0 (la valeur Q est de l’ordre du MeV tandis que l’énergie de masse vaut plusieurs dizaines voire centaines de MeV). Il est alors possible d’appliquer un développement limité à l’ordre 1 ce qui conduit à la relation .
Noyau de recul
La conservation de la quantité de mouvement permet de démontrer que l’énergie cinétique du noyau de recul, , s’exprime habituellement à l’aide de la relation suivante[20]
où est l’énergie du neutrino associée à une couche électronique donnée, est la masse du noyau fils Y (après la désintégration) et est la vitesse de la lumière dans le vide.
Cette relation s’obtient directement de la conservation de la quantité de mouvement en supposant un neutrino sans masse et en négligeant les effets relativistes. Le noyau père étant au repos au moment de la désintégration (sa quantité de mouvement est nulle), on peut écrire . Par ailleurs, l’énergie cinétique du noyau de recul s’exprime par la relation suivante : . Les quantités de mouvement des deux corps en jeu (le neutrino et le noyau de recul) étant égales, on obtient . Enfin, le neutrino étant considéré comme sans masse, sa quantité de mouvement s’exprime par la relation . On obtient ainsi la relation
Cette quantité est généralement négligeable sauf dans le cas du ⁷Be où l’énergie de recul du ⁷Li vaut 57 eV dans le cas d’une capture d’un électron de la couche K. Cette énergie de recul a été mesurée pour la première fois en 1997 par Massimiliano Galeazzi et ses collaborateurs[21].
Réarrangement du cortège électronique

Un proton libre ne peut se désintégrer en neutron par capture électronique ; les protons et les neutrons doivent faire partie d’un noyau. Lors de la capture électronique, un électron situé sur une orbitale atomique, habituellement les couches K ou L, est capturé par le proton conduisant à la décroissance du noyau. La capture de l’électron crée un trou sur l’orbitale où il se trouvait. Les électrons se réarrangent alors sur les couches afin de remplir à nouveau les orbitales de plus basses énergies. Différentes transitions électroniques ont alors lieu jusqu’à ce que l’ensemble des couches soient pleines. Chaque transition (passage d’un électron d’une couche donnée à une couche d’énergie inférieure) est accompagnée par l’émission d’un photon X ou d’un électron Auger.
L’énergie du photon X ou de l’électron Auger correspond exactement à la différence d’énergie entre les deux niveaux électroniques. En supposant la capture d’un électron de la couche K par le proton et la transition d’un électron de la couche L vers la couche K pour combler la lacune, alors l’énergie du photon X émis, EX, est donnée par la relation :
- EX = EK - EL
où EK et EL sont respectivement l’énergie des couches K et L. Au lieu d’émettre un photon X, il est également possible de transférer ce surplus d’énergie à un autre électron du cortège électronique qui sera alors expulsé de l’atome ; il s’agit de l’effet Auger. L’énergie de cet électron, Ee, est alors donnée par (en supposant qu’il se trouve sur la couche M) :
- Ee = EK - EL - EM
où EM est l’énergie de la couche M.
Le réarrangement atomique complet peut donc être accompagné de plusieurs émissions d’électrons Auger et/ou de photons X. Il est par ailleurs possible que la lacune initiale soit comblée par un électron libre. Un unique photon X (ou un unique électron Auger) est alors émis avec une énergie égale à l’énergie du niveau sur lequel a été faite la lacune.
Temps de demi-vie
Les temps de demi-vie relativement longs observés dans le cadre de la capture électronique s’expliquent par le fait que ce processus est gouverné par l’interaction faible. Ainsi, les temps de demi-vie les plus courts sont de l’ordre de la milliseconde (10−3 s), à comparer aux temps de demi-vie des états excités d’un noyau, gouvernés par l’interaction forte, de l’ordre de 10−21 s pour les plus courts. Deux facteurs influent particulièrement sur le temps de demi-vie[22] :
- la valeur Q : plus elle est grande, plus le temps de demi-vie est court ;
- la structure nucléaire des noyaux père et fils : plus la différence de spin[Note 2] entre les états initial et final est faible, plus le temps de demi-vie est court. Cela permet ainsi d’expliquer le temps de demi-vie du ⁴¹Ca qui est d’environ 100 000 ans. En effet, l’état fondamental du ⁴¹Ca a un spin de 7/2 ħ et une parité négative tandis que son noyau fils, le ⁴¹K, a un état fondamental avec un spin de 3/2 ħ et une parité positive. La différence de spin de 2ħ ainsi que le changement de parité explique la désintégration relativement lente de ce noyau.
En plus de ces deux facteurs, il faut en ajouter un troisième qui correspond à la probabilité de trouver un électron dans le noyau atomique. En général, cette probabilité est la plus importante pour les électrons se trouvant sur les couches électroniques les plus internes (couches K, L, M, … par ordre d’importance)[Note 1]. Ainsi, plus le nombre quantique principal d’un électron est grand, plus sa probabilité de présence à l’intérieur du noyau est faible. Il est en de même pour le nombre quantique secondaire ; plus celui-ci est grand, plus la fonction d'onde de l’électron sera diffuse réduisant de ce fait la probabilité de présence dans le noyau[23].
Les électrons des couches les plus internes sont globalement plus près du noyau dans les noyaux les plus lourds (ceux avec un grand numéro atomique) ce qui explique pourquoi le temps de demi-vie des noyaux lourds décroissant par capture électronique est globalement plus court que ceux des noyaux plus légers.
Milieu compressé
La première étude concluante de l’influence de la compression des atomes sur le taux de capture électronique a été réalisée par R. F Leininger, E. Segrè et C. Wiegand en 1949[24]. Dans cette étude, la décroissance du ⁷Be a été mesurée lorsque des atomes de ce dernier étaient présents sous la forme d’oxyde de béryllium, BeO, et sous forme de fluorure de béryllium, BeF₂. L’étude a montré que la constante de désintégration du béryllium 7 était différente lorsqu’il était présent à l’intérieur d’une matrice cristalline (le fluorure de béryllium) et lorsqu’il était seul ; la constante de décroissance du ⁷Be présent dans le fluorure de béryllium est 0,16 % plus petite que celle du ⁷Be libre. D’autres études sur le béryllium ont montré que l’écart entre les constantes de décroissance pouvait attendre 1 % dans d’autres matériaux[25]. Cette diminution de la constante de décroissance vient du fait que la capture électronique devient plus probable lorsque l’atome est compressé, les électrons étant plus proches du noyau.
En géochimie, il a été supposé que de fortes pressions pourraient augmenter le taux de décroissance du potassium 40 (qui se désintègre en argon 40), faussant ainsi la datation par le potassium-argon. Il est cependant admis que des pressions moins importantes auraient un effet sur la rétention de l’argon bien avant de pouvoir influencer le taux de décroissance du potassium[26].
Atome ionisé
Tout comme la conversion interne, ce processus ne peut avoir lieu si l’atome est entièrement ionisé, étant donné qu’aucun électron ne pourra être capturé par le noyau. Cela permet d'expliquer pourquoi le 7Be est stable dans le rayonnement cosmique[27]. En revanche, plusieurs études ont montré que le temps de demi-vie d’un noyau décroissant uniquement par capture électronique augmentait lorsqu’il est pratiquement ionisé[28] - [29]. Ces études ont montré qu’un atome hydrogénoïde, c’est-à-dire un atome n’ayant plus qu’un seul électron, a une constante de décroissance environ deux fois plus grande que celle d’un atome héliumoïde (un atome n’ayant que 2 électrons) ; l’héliumoïde décroit donc deux fois moins vite que l’hydrogénoïde. Ce résultat est en contradiction avec le sens commun qui voudrait que la probabilité de décroitre soit deux fois plus importante lorsqu’il y a deux électrons plutôt qu’un seul. Des travaux théoriques permettent de reproduire ces résultats, essentiellement en tenant compte de la conservation du moment angulaire dans le système noyau plus électron[30] - [31].
Il a par ailleurs été montré dans ces deux expériences que l’atome neutre décroît également moins vite que l’atome hydrogénoïde. L’explication est la même que dans le cas de l’héliumoïde[28] - [29].
Compétition entre la capture électronique et l’émission de positron
Seuil pour l’émission de positron
Tout comme la capture électronique, l’émission de positron peut avoir lieu dans les noyaux déficients en neutrons. D’un point de vue énergétique, cette dernière ne peut avoir lieu que si la masse du noyau père est supérieure d’au moins 1,022 MeV/c2 à la masse du noyau fils. La raison est la suivante. Dans la réaction :
le noyau X possède Z électrons tout comme le produit de décroissance primaire Y, qui a un proton de moins dans son noyau atomique que X. Le noyau fils Y est donc ionisé négativement juste après la décroissance par émission de positron. L’électron supplémentaire sera donc relâché et doit être pris en compte dans le bilan énergétique de la réaction. L’énergie de la décroissance, la valeur Q, qui correspond à la différence d’énergie entre le système final et le système initial, s’écrit :
Seules les réactions exothermiques se produisent spontanément puisqu’elles ne nécessitent pas l’apport d’énergie extérieure. Ainsi, pour que l’émission de positron soit possible, faut-il que Q soit négatif. C’est le cas si :
En négligeant la masse du neutrino électronique, inférieure à 1,1 eV/c2 d’après la dernière évaluation du Particle Data Group[32], on en déduit que l’émission de positron n’est possible que lorsque la différence de masse entre le noyau père et noyau fils est supérieure à deux fois la masse de l’électron (l’électron et le positron ont la même masse, 511 keV/c2), soit 1,022 MeV/c2.
Compétition
Ainsi la capture électronique est-elle le seul mode de décroissance à la disposition des noyaux déficients en neutrons pour lesquels l’émission de positron est impossible. Au-delà de ce seuil, il existe une compétition entre la capture électronique et l’émission de positron. Dans les grandes lignes, le rapport entre la probabilité de décroitre par capture électronique, Pε, et celle de décroitre par radioactivité β+, Pβ+, est[22] :
Cela se comprend par le fait que d’une part la probabilité de présence dans le noyau d’un électron 1s augmente avec le numéro atomique et que d’autre part, la création du positron, qui est une particule chargée positivement, n’est pas favorable du fait de la répulsion coulombienne avec les protons du noyau, d’autant plus importante que le nombre de protons est élevé.
Plus précisément, le rapport entre les deux probabilités est donné par[33] :
pour une transition permise, et :
pour une transition interdite unique, où :
- qK est l’énergie du neutrino associé à l’électron de la couche K ;
- f et g sont des composantes des fonctions d’onde radiale de l’électron ;
- B est un facteur d’échange ;
- ΔJ est la différence entre le moment angulaire initial et final ;
- PK, PL, PM, … sont respectivement les probabilités de capturer un électron de la couche électronique K, L, M, …
Utilisation de la capture électronique
Scintigraphie au gallium
Le gallium 67 a un temps de demi-vie d’environ 3 jours[34] et décroit uniquement par capture électronique vers des états excités du zinc 67 qui émet alors des photons gamma afin d’atteindre son état fondamental. Ces photons sont utilisés dans la scintigraphie au gallium. Cette technique d’imagerie médicale est utilisée lorsqu’une technique concurrente, la tomographie par émission de positons, n’est pas disponible[35]. Le gallium 67 est ainsi utilisé du fait de ces propriétés chimiques, de son temps de demi-vie relativement adéquat et de sa décroissance qui conduit à l’émission de rayons gamma.
Datation par le potassium-argon
Le potassium 40 décroit par capture électronique en argon 40. Ce mode de décroissance est utilisée pour dater la formation de certaines roches contenant du potassium, en supposant nulle la quantité initiale d’argon 40 dans ces roches et que l’argon 40 y reste piégé une fois formé.
Notations et désignation
Ce processus est parfois appelé désintégration bêta inverse[36] - [37], bien que ce terme puisse aussi référer à l’interaction entre un antineutrino électronique et un proton[38] - [39].
Concernant la notation, celle qui est la plus couramment utilisée est celle qui suit :
L’électron qui est capturé est l’un des électrons présents dans le cortège électronique de l’atome ; il ne s’agit donc pas d’une collision entre le noyau et un électron qui arriverait de l’extérieur, comme pourrait le suggérer la notation de la réaction ci-dessus. La notation est en effet ambigüe car elle est identique à un autre phénomène, nommé ionisation par impact électronique[40]. Ce phénomène correspond à la capture d’un électron, provenant de l’extérieur de l’atome, par un atome ou une molécule. Ce phénomène a principalement lieu dans les plasmas. Pour distinguer les deux phénomènes, on rencontre parfois[41] - [42] l’écriture suivante pour représenter la capture électronique orbitale :
où l’indication qu’il s’agit du processus nucléaire de la capture électronique est donnée par le « CE » au-dessus de la flèche.
Exemples courants
En 1977, Walter Bambynek avait relevé l’existence d’environ 500 noyaux qui décroissent partiellement ou uniquement par capture électronique[43]. Parmi ceux-ci, voici une liste des principaux radioisotopes qui décroissent uniquement par capture électronique et qui ont un temps de demi-vie supérieur à 1 an :
| Radioisotope | Temps de demi-vie |
|---|---|
| 26Al | (7,17 ± 0,24) × 10⁵ années[44] |
| 41Ca | (1,002 ± 0,017) × 10⁵ années[45] |
| 44Ti | 60,0 ± 1,1 années[46] |
| 53Mn | (3,74 ± 0,04) × 10⁶ années[47] |
| 55Fe | 2,747 ± 0,008 années[48] |
| 59Ni | (76 ± 5) × 10³ années[49] |
| 81Kr | (2,29 ± 0,11) × 10⁵ années[47] |
| 91Nb (nl) | (6,8 ± 1,3) × 10² années[47] |
| 93Mo (ia) | (4,0 ± 0,8) × 10³ années[47] |
| 97Tc | (4,21 ± 0,16) × 10⁶ années[47] |
| 101Rh (nl) | 3,3 ± 0,3 années[47] |
| 109Cd (nl) | 461,9 ± 0,4 jours[50] |
| 133Ba (ia) | 10,540 ± 0,006 années[51] |
| 137La (nl) | (6 ± 2) × 10⁴ années[47] |
| 145Pm (nl) | 17,7 ± 0,4 années[47] |
| 146Pm (nl) | 5,53 ± 0,5 années[47] |
| 150Eu (nl) | 36,9 ± 0,9 années[47] |
| 157Tb (ia) | 71 ± 7 années[47] |
| 163Ho | 4570 ± 25 années[47] |
| 173Lu (ia) | 1,37 ± 0,01 années[47] |
| 174Lu (ia) | 3,31 ± 0,05 années[47] |
| 172Hf (ia) | 1,87 ± 0,03 années[47] |
| 179Ta | 1,82 ± 0,03 années[47] |
| 193Pt (ia) | 50 ± 6 années[47] |
| 194Hg | 444 ± 77 années[47] |
| 202Pb | (52,5 ± 2,8) × 10³ années[47] |
| 205Pb | (1,73 ± 0,07) × 10⁷ années[47] |
| 208Bi | (3,68 ± 0,04) × 10⁵ années[47] |
Autres processus liés
Capture électronique radiative
Comme c’est le cas pour l’ensemble des processus de désintégration bêta, il peut arriver que la capture électronique soit accompagnée de l’émission d’un photon gamma en plus du neutrino. L’énergie du neutrino ne prend alors plus une valeur unique mais suit une distribution, puisque l’énergie disponible est partagée entre trois corps. Ce rayon gamma peut être compris comme une sorte de « bremsstrahlung interne » qui a lieu lorsque l’électron capturé interagit électromagnétiquement avec le noyau. La présence de photons accompagnant les désintégrations bêta était connue depuis G. H. Aston en 1927[52]. Dix ans plus tard, Christian Møller indique que ce phénomène devrait également avoir lieu dans la capture électronique[53]. La première observation expérimentale de la capture électronique radiative a été publiée par H. Bradt et al. en 1946[54].
La première description théorique du phénomène a été donnée par Philip Morrison et Leonard I. Schiff (en) dans un papier publié en 1940[55].
Double capture électronique
La double capture électronique est un processus de désintégration au cours duquel deux captures électroniques orbitales ont lieu simultanément. La réaction s’écrit :
Ce mode de décroissance ne peut se produire que si la masse du nucléide fils est inférieure à celle du nucléide père. En pratique, ce mode de décroissance, tout comme la double désintégration bêta, est très lent ; son observation n’est ainsi possible que lorsque les autres modes de décroissance, beaucoup plus probables, ne peuvent avoir lieu. Les temps de demi-vie sont ainsi très grands avec des valeurs de l’ordre de 1020 années. En 2014, seule la décroissance du baryum 130 par double capture électronique avait pu être mise en évidence sur la base d’arguments géochimiques[56] - [57] - [58]. En 2019, la décroissance du xénon 124 est observée avec une demi-vie, la plus longue jamais mesurée, de (1,8 ± 0,6) × 1022 ans[59] - [60] (1 300 milliards de fois l'âge de l'Univers).
Capture muonique
Le muon est un lepton — tout comme l’électron — appartenant à la deuxième génération (tandis que l’électron appartient à la première). En remplaçant des électrons appartenant au cortège électronique de l’atome par des muons, la capture d’un muon par le noyau conduit à la réaction suivante :
où µ désigne le muon, X le noyau père, Y le noyau fils et νμ le neutrino muonique. Le noyau fils est créé dans un état excité. Pour atteindre son état fondamental, il émet des photons et/ou des particules tels que des protons, des neutrons, des particules alpha…
Article connexe
Notes et références
Notes
- Il existe cependant des exceptions comme le 40K dont la probabilité de capturer un électron L est plus grande que celle de capturer un électron K[18].
- Comme souvent, on désigne ici par spin le moment angulaire total, c’est-à-dire la somme du moment angulaire orbital et du spin du ou des nucléons qui peuplent l’état.
Références
- Irène Curie, F. Joliot. Nouvelles recherches sur l’émission des neutrons. J. Phys. Radium, 1933, 4 (6), p. 278-286.
- (en) Na-22 table[PDF], nucleide.org.
- (it) G. C. Wick Rendiconti Accad. Lincei 19, 319 (1934).
- (en) Luis W. Alvarez, W. Peter Trower (1987). "Chapter 3: K-Electron Capture by Nuclei (with the commentary of Emilio Segré)" In Discovering Alvarez: selected works of Luis W. Alvarez, with commentary by his students and colleagues. University of Chicago Press, p. 11–12, (ISBN 978-0-226-81304-2).
- I. Curie et F. Joliot, C. R. Acad. Sci. 198, 254 (1934).
- (en) H. Bethe et R. Peierls, The Neutrino, Nature* 133, 689-690 () DOI 10.1038/133689b0.
- (en) H. Yukawa et S. Sakata, On the Theory of the β-Disintegration and the Allied Phenomenon. Proc. Phys.-Math. Soc. Japan 1935; 17: 467-479.
- (en) Luis Alvarez, The Nobel Prize in Physics 1968, biography, nobelprize.org. Accessed on line October 7, 2009.
- (en) Nuclear K Electron Capture, Luis W. Alvarez, Physical Review 52 (1937), p. 134–135, DOI 10.1103/PhysRev.52.134 .
- (en) Electron Capture and Internal Conversion in Gallium 67, Luis W. Alvarez, Physical Review 53 (1937), p. 606, DOI 10.1103/PhysRev.53.606.
- (en) The Capture of Orbital Electrons by Nuclei, Luis W. Alvarez, Physical Review 54 (October 1, 1938), p. 486–497, DOI 10.1103/PhysRev.54.486.
- (en) Kirkwood, D. H. W. , B. Pontecorvo, et G. C. Hanna, 1948, Fluctuations of Ionization and Low Energy Beta-Spectra, Phys. Rev. 74, 497 DOI 10.1103/PhysRev.74.497.
- (en) Pontecorvo, B. , D. H. W. Kirkwood, et G. C. Hanna, 1949, Nuclear Capture of LI Electrons, Phys. Rev. 75, 982 DOI 10.1103/PhysRev.75.982.
- (en) Peter W. Dougan, Proportional counter studies of orbital electron capture ratios, University of Glasgow, (lire en ligne).
- (en) Alex F Bielajew, Lecture Notes for Chapter 15: β decay[PDF], diapositive 16, 2012.
- (en) Kramida, A., Ralchenko, Yu., Reader, J., et NIST ASD Team (2014). NIST Atomic Spectra Database (ver. 5.2), [Online]. Available: http://physics.nist.gov/PhysRefData/ASD/ionEnergy.html [2015, January 31]. National Institute of Standards and Technology, Gaithersburg, MD.
- (en) Alex F Bielajew, Lecture Notes for Chapter 15: β decay[PDF], diapositive 18, 2012.
- (de) « Der Elektroneneinfang des K40 », Zeitschrift für Naturforschung A, vol. 9, no 5, , p. 469—472 (DOI 10.1515/zna-1954-0514, lire en ligne)
- (en) Am-244m table[PDF], nucleide.org.
- (en) Table de RADIONUCLÉIDES[PDF], page 19, 2011.
- (en) M. Galeazzi et al., Lithium versus chlorine: for the solution of the solar neutrino problem, Physics Letters B 398 (1997), 187-193 DOI 10.1016/S0370-2693(97)00255-4.
- (en) SECTION 11: Beta Decay[PDF], page 8-9.
- (en) SECTION 11: Beta Decay[PDF], pages 6-7.
- (en) R. F Leininger, E. Segre et C. Wiegand, Experiments on the effect of atomic electrons on the decay constant of ⁷Be[PDF], 1949.
- (en) A. Ray, P. Das, S. K. Saha, A. Goswami, A. De, Enhanced orbital electron-capture nuclear decay rate in compact medium[PDF], arXiv:0904.0326, .
- (en) Carla W. Montgomery, « Electron capture », dans Clare P. Marshall, Rhodes W. Fairbridge, Encyclopedia of geochemistry, Kluwer Academic Publishers, (ISBN 0-412-75500-9), p. 189.
- F. Yiou, F. Guchan-Beck. Stabilité de 7Be dans le rayonnement cosmique galactique. Journal de Physique, 1969, 30 (5-6), p. 401-405. DOI 10.1051/jphys:01969003005-6040100.<jpa-00206798>.
- (en) Yu. A. Litvinov et al., Measurement of the β+ and Orbital Electron-Capture Decay Rates in Fully Ionized, Hydrogenlike, and Heliumlike ¹⁴⁰Pr Ions, Phys. Rev. Lett. 99, 262501, 2007 DOI 10.1103/PhysRevLett.99.262501.
- (en) N. Winckler et al., Orbital electron capture decay of hydrogen- and helium-like 142Pm ions, Physics Letters B Volume 679, Issue 1, 10 August 2009, Pages 36–40 DOI 10.1016/j.physletb.2009.07.019.
- (en) Zygmunt Patyk et al., « Orbital electron capture decay of hydrogen- and helium-like ions », Phys. Rev. C, vol. 77, , p. 014306 (DOI 10.1103/PhysRevC.77.014306, lire en ligne).
- (en) Andrei N. Ivanov et al., « Weak decays of H-like140 Pr58+ and He-like140 Pr57+ ions », Phys. Rev. C, vol. 78, , p. 025503 (DOI 10.1103/PhysRevC.78.025503, lire en ligne).
- (en) R.L. Workman et al. (Particle Data Group) (Particle Data Group), Review of Particle Physics, Prog. Theor. Exp. Phys. 2022, numéro 8, (août 2022), page 1274.
- (en) Table of Radionuclides[PDF], page 22, 2011.
- (en) Ga-67 table[PDF], nucleide.org.
- Pourquoi on fait une scintigraphie au gallium, cancer.ca (en).
- Richard Taillet, Pascal Febvre et Loïc Villain, Dictionnaire de physique, Bruxelles/Paris, De Boeck Supérieur, , 741 p. (ISBN 978-2-8041-0248-7, lire en ligne), p. 74.
- (en) Robert J. Tuttle, The Fourth Source : Effects of Natural Nuclear Reactors, Universal-Publishers, , 580 p. (ISBN 978-1-61233-077-8, lire en ligne), p. 6.
- « Le neutrino, une particule fantôme », sur in2p3.fr.
- Dispositions testamentaires de Georges Lochak[PDF], page 34, .
- Julien Lecointre, Ionisation et dissociation par impact électronique d’ions moléculaires d’intérêt atmosphérique et thermonucléaire, Presses universitaires de Louvain, 2007, (ISBN 978-2-87463-094-1).
- (en) Dr. B. K. Sharma, Nuclear and Radiation Chemistry, page 27, 2001.
- (en) Michael F. L’Annunziata, Handbook of Radioactivity Analysis, page 57, 2012.
- (en) W. Bambynek et al., Orbital electron capture by the nucleus, Rev. Mod. Phys. 49, 77 (1977), page 80 DOI 10.1103/RevModPhys.49.77.
- (en) Al-26 table[PDF], nucleide.org.
- (en) Ca-41 table[PDF], nucleide.org.
- (en) Ti-44 table[PDF], nucleide.org.
- (en) National Nuclear Data Center, « information extracted from the Chart of Nuclides database ».
- (en) Fe-55 table[PDF], nucleide.org.
- (en) Ni-59 table[PDF], nucleide.org.
- (en) Cd-109 table[PDF], nucleide.org.
- (en) Ba-133 table[PDF], nucleide.org.
- (en) Aston, G.H., 1927. The Amount of Energy Emitted in the γ-Ray Form by Radium E[PDF] Proc. Cambridge Philos. Soc. 23, 935–941 DOI 10.1017/S0305004100013815.
- (de) Møller, C., 1937, Einige Bemerkungen zur Fermischen Theorie des Positronenzerfalls, Physikalische Zeitschrift der Sowjetunion 11, 9.
- (de) Bradt, H. , P. C. Gugelot, O. Huber, H. Medicus, P. Preiswerk, P. Scherrer, et R. Steffen, 1946, K-Einfang des Fe55, Helvetica Physica Acta 19, 222.
- (en) P. Morrison et L. I. Schiff, Radiative K Capture, Phys. Rev. 58, 24, 1940 DOI 10.1103/PhysRev.58.24
- (en) A.S. Barabash et R.R. Saakyan, Experimental limits on 2beta+, K beta+, and 2K processes for Ba-130 and on 2K capture for Ba-132, Phys. At. Nucl. (nl) 59 (1996) 179.
- (en) A.P. Meshik et al., Weak decay of 130Ba and 132Ba: Geochemical measurements, Phys. Rev. C 64 (2001) 035205 DOI 10.1103/PhysRevC.64.035205.
- (en) M. Pujol. B. Marty, P. Burnard, et P. Philippot, Xenon in Archean barite: Weak decay of 130Ba, mass-dependent isotopic fractionation and implication for barite formation, Geoch. Cosm. Act. bf vol. 73 (2009) 6834. DOI 10.1016/j.gca.2009.08.002.
- (en) Andrew Grant, « A decay with an extraordinary half-life », Physics Today, (DOI 10.1063/PT.6.1.20190503a, lire en ligne, consulté le ).
- (en) Collaboration XENON, « Observation of two-neutrino double electron capture in 124Xe with XENON1T », Nature, vol. 568, (DOI 10.1038/s41586-019-1124-4).
![Q = M_{{}_{Z}^{A}X}c^2 - M_{{}_{Z-1}^{A}Y}c^2 + E^* - B^X_n + \left[ \sum_{i=1}^Z B^X_i - \sum_{i=1}^{Z-1} B^Y_i \right]](https://img.franco.wiki/i/b3c686d7b177776c013dc46216a00416a7db6c42.svg)




![\left[ \sum_{i=1}^Z B^X_i - \sum_{i=1}^{Z-1} B^Y_i \right]](https://img.franco.wiki/i/9071c4ad6b817ba2e68193cd7edff78d94344ec9.svg)



![M_{{}_{Z}^{A}X}c^2 - M_{{}_{Z-1}^{A}Y}c^2 + E^* - B^X_n + \left[ \sum_{i=1}^Z B^X_i - \sum_{i=1}^{Z-1} B^Y_i \right] > 0](https://img.franco.wiki/i/d1412134bade91cc1b2e3fd844bfe0bc4cb20f18.svg)





























![\frac{P_\epsilon}{P_{\beta^+}} = \frac{\pi}{2} \frac{q^2_K g^2_K B_K}{f_0} \left[ 1 + \frac{P_L}{P_K} + \frac{P_M}{P_K} + ...\right]](https://img.franco.wiki/i/926c76c1ba1d6ff1358f8067267512de9ca787b8.svg)
![\frac{P_\epsilon}{P_{\beta^+}} = \frac{\pi}{2} \frac{q^{2\Delta J}_K g^2_K B_K}{f_{\Delta J-1}} \left[ 1 + \frac{P_L}{P_K} + \frac{P_M}{P_K} + ...\right]](https://img.franco.wiki/i/fc69eabb657c2bc29ecda8e5cb0643e4bed586a1.svg)
