Baguettes à calculer
Les baguettes à calculer (chinois : 算筹/算籌, pinyin : suànchóu) sont des bâtonnets d'environ 10 cm de long[1] utilisés par les Chinois dès le IIIe siècle av. J.-C. pour effectuer des calculs. Le système s'appuie sur une représentation des nombres selon une numération décimale positionnelle.

Ce système précède de plusieurs siècles le système de calcul avec boulier. Il permet des opérations simples comme les additions et les soustractions, mais aussi des opérations plus complexes comme les multiplications, les divisions, les extractions de racines. Avec l'introduction d'une représentation spéciale pour les nombres négatifs, il permet de travailler sur des notions plus abstraites comme la résolution de systèmes d'équations linéaires, le calcul sur les coefficients de polynômes, avec la méthode de Ruffini-Horner, ou la représentation de polynômes à deux variables.
Histoire
La description la plus ancienne de ce système se trouve dans l'ouvrage Hanshu (Histoire des Hans) rédigé par Ban Gu au Ier siècle av. J.-C. Ce système est appelé selon les sources suan, ou chou ou chousuan ou suanchou, suanzi durant la dynastie des Song, le terme suan ayant probablement le sens de baguette[2]. Mais l'usage d'un tel système de calcul est probablement antérieur au Ier siècle av. J.-C.. On trouve en effet des références à un procédé de calcul externe dans des ouvrages plus anciens : dès le Livre des procédures mathématiques (Suanshushu - antérieur à 186 av. J.-C.), on voit apparaitre l'expression «placer le nombre» lors du début de la procédure laissant suggérer l'existence d'une action physique à effectuer[3]. Volkov[2] place donc l'usage des baguettes pour les calculs au plus tard au IIIe siècle av. J.-C..

Plus on progresse dans les siècles et plus les références à ce système se font précises. L'astronome Liu Xin (en), au Ier siècle, précise que l'on effectuait des calculs astronomiques à l'aide d'un jeu de 271 baguettes d'environ 14 cm de long et que ces baguettes servaient également dans la numérologie et la divination[4]. Le Classique mathématique de Sunzi (IVe siècle) décrit avec précision le système de représentation et les procédures de calcul. Lorsque, entre les dynasties Tang et Song, autour du Xe siècle, des illustrations sont insérées dans les ouvrages, on a trace, non seulement du procédé d'écriture, mais aussi de la disposition des lignes de calculs lors des opérations[5].

Les calculs effectués avec les baguettes nécessitent une surface plane sur laquelle seraient matérialisées des cases indiquant les diverses décimales et où seraient posées les baguettes. Certains historiens (Li Yan, Joseph Needham, Ulrich Libbrecht (en)) ont émis l'hypothèse que cette surface plane serait une planche en bois, découpée en cases[6]. Cependant aucune planche de ce type n'a été retrouvée dans les fouilles archéologiques. De plus, une telle planche devrait être d'une très grande taille pour pouvoir exécuter des calculs avec de très grands nombres. Il semble donc plus raisonnable de penser, selon Chemla[7] et Volkov[6], que les calculs se faisaient simplement sur le sol ou sur une table, les cases étant seulement imaginées ou bien reproduites sur une toile ou une feuille de papier aisément transportables.
Le développement d'algorithme de calcul s'effectuant dynamiquement dans des cases d'un tableau s'étend naturellement au calcul de fractions puis aux algorithmes de résolution de systèmes d'équations avec introduction des nombres négatifs (IIIe siècle[8]) puis aux calculs sur les polynômes avec recherche de racines selon la méthode de Ruffini-Horner et la résolution de systèmes d'équations non linéaires (XIIIe siècle)[9].
On peut dater la disparition des baguettes pour les calculs entre le XVe siècle et XVIe siècle, remplacées progressivement par l'usage du boulier[9] et la pratique du calcul écrit.
Numération
Il s'agit d'une numération de position à base 10 comportant dix-huit symboles, avec un vide pour représenter le zéro. Le principe consiste à représenter à l'aide de baguettes des chiffres de 1 à 9 . La position du chiffre en question disposé sur une surface de calcul indique son ordre de grandeur (de gauche à droite : ..., millier, centaine, dizaine, unité, dixième, centième ...). L'absence de baguette dans une case indique l'équivalent de zéro. Les opérations s'effectuent en déplaçant les baguettes ou en modifiant leur configuration.
Chiffres
La numération à bâtons possède deux séries de chiffres allant de 1 à 9. Dans cet article, l'une des deux séries sera identifiée par la lettre A et l'autre par la lettre B. Dans les deux séries, le 0 est représenté par un espace vide.
| Série | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | ||||||||||
| B | ||||||||||
Construction de nombres
En tant que système positionnel à base 10, chaque chiffre représente un coefficient d'une puissance de 10 selon la place qu'il occupe. Le chiffre le plus à droite est l'unité du nombre, celui à sa gauche, la dizaine, etc.
Cependant, le chiffre zéro représenté par un vide pose problème : deux nombres tels 62 et 620 seraient difficilement distinguables.
De plus, lorsque l'on pose les bâtons, si ![]() représente le chiffre 2 et
représente le chiffre 2 et ![]() représente le chiffre 1, il n'est pas évident de savoir si
représente le chiffre 1, il n'est pas évident de savoir si ![]() représente 3, 12 ou 21 (ou même 30, 120 ou 210).
représente 3, 12 ou 21 (ou même 30, 120 ou 210).
C'est pour pallier ces confusions possibles que la numération possède deux séries de chiffres.
La série A sert à noter les chiffres des puissances paires de 10 (unités, centaines, dizaines de milliers, ...) et la série B est utilisée pour les puissances de 10 impaires (dizaines, milliers, ...).
Ainsi, les nombres suivants sont représentées par :
- 4 :

- 72 :


- 256 :



- 308 :



- 1 007 :




- 81 753 :





- 1,95 :



Il n'y a pas de moyen (comme dans la numération babylonienne) de différencier les nombres décimaux des entiers. Seuls leur position sur la table à calcul et le texte qui les accompagne les différencient. Dans certains ouvrages, l'unité principale est signalée par un symbole placé sous le chiffre des unités[10]. Ainsi l'écriture :
| 日 |
avec l'idéogramme 日 (jour) placé sous le premier 1, signifie que le nombre représenté est 1,1446154 jour.
Les zéros consécutifs sont symbolisés par un espace d'autant plus grand qu'ils sont nombreux.
Fractions
Une fraction est représentée à l'aide de deux lignes, la supérieure contenant le numérateur et l'inférieure le dénominateur. Cette représentation est probablement inspirée de l'algorithme de division à l'issue duquel le résultat de la division se présente sur 3 lignes : dans la ligne 1 figure la partie entière du quotient, la partie fractionnaire occupant les lignes 2 (pour le numérateur) et 3 (pour le dénominateur)[11]. Ainsi la fraction mixte 132⁄7 se représente par :
Nombres négatifs
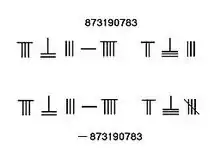
Quand apparaissent les nombres négatifs comme coefficients dans les polynômes ou les systèmes d'équations linéaires, il s'agit de trouver un moyen de les différencier des nombres positifs. Cela peut se faire en utilisant une couleur différente pour les positifs et les négatifs (rouge vs. noir, ou noir vs. blanc) ou en plaçant les nombres négatifs en oblique[12] ou encore en utilisant des baguettes de sections différentes[4]. Dans les ouvrages écrits, on trouve également le nombre négatif identifié par un trait venant barrer le chiffre non nul le plus à droite[13] - [14].
Zéro
Avec le système de baguettes, le zéro est symbolisé par un vide. Cependant, lorsque des illustrations de calculs sur surface à calculer viennent compléter les algorithmes dans les ouvrages papier, on voit apparaitre une représentation de l'absence de baguettes par un rond (XIIIe siècle[15]). Ce symbole est probablement inspiré de la notation du zéro indien[14] sous forme de point[15].
Calculs
Addition et soustraction
Comme pour les calculs avec boulier, les opérations s'effectuent à partir des poids les plus forts (de gauche à droite), les retenues étant immédiatement reportées.
Concernant les additions de fractions a⁄b+c⁄d, il faut placer les numérateurs (a et c) à gauche, les dénominateurs (b et d) à droite. On réduit ensuite les fractions au même dénominateur en multipliant a par d, puis c et d par b. On ajoute les deux nombres de gauche (qui contiennent respectivement ad et bc) et on met le résultat en haut à droite[16].
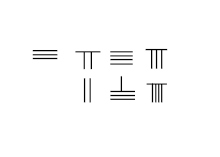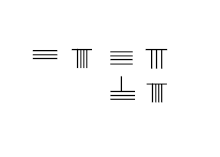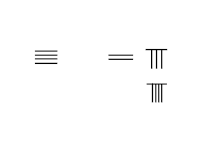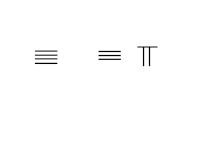 Addition avec retenue:3748+289=4037 |
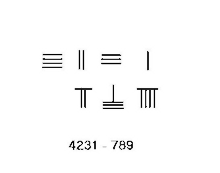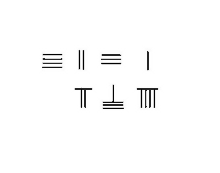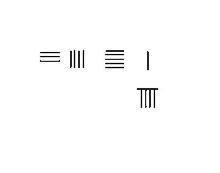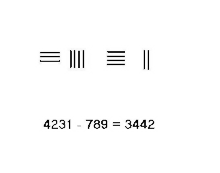 Soustraction avec retenue : 4231-789 = 3442 |
 Somme de deux fractions : 1⁄3+2⁄5=11⁄15 |
Multiplication et division
La multiplication nécessite trois lignes. Sur la première ligne est écrite le multiplicande. Sous la ligne du multiplicande, on écrit progressivement le produit des deux nombres. Le multiplicateur se positionne successivement sous chaque chiffre du multiplicande dans la troisième ligne. On multiplie le premier chiffre le plus à gauche du multiplicande par le multiplicateur. Le produit est placé dans la ligne médiane, sous le chiffre du multiplicande. On supprime alors le premier chiffre du multiplicande, on décale le multiplicateur vers la droite et on multiplie le second chiffre du multiplicande par ce multiplicateur, le résultat vient s'ajouter au nombre situé dans la ligne médiane et ainsi de suite[17].
La division procède selon le même principe. Le dividende est inscrit dans la ligne médiane. Le diviseur se place successivement le plus à gauche possible sous la ligne du dividende. On opère la division de la partie gauche du dividende par le diviseur, le quotient (chiffre de 1 à 9) est placé dans la ligne supérieure , au-dessus du chiffre des unités du diviseur, la partie du dividende est remplacée par le reste de la division. On décale alors le diviseur vers la droite pour recommencer l'opération[18] - [17].
La multiplication de nombres fractionnaires commence par la transformation des nombres ab⁄c(forme mixte) en (ac+b)⁄c (forme impropre), puis on multiplie entre eux les numérateurs, et entre eux les dénominateurs et on effectue une division classique[19].
La division des fractions commence par leur transformation de mixtes en impropres, une réduction au même dénominateur et une division d'un numérateur par l'autre[20]. Liu Hui propose une réduction des deux dernières étapes[20] : a⁄b div c⁄d = ad⁄bc
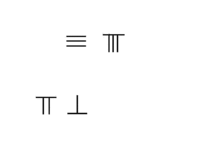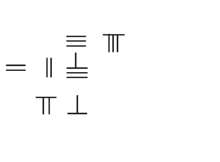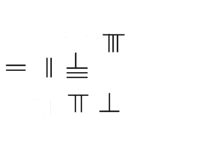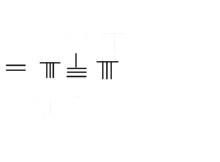 Multiplication :38 × 76=2888 |
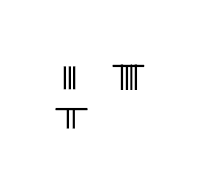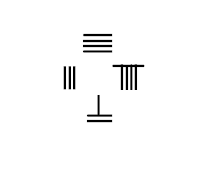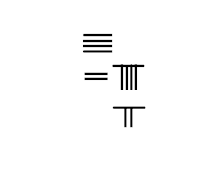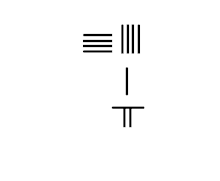 Division : 309⁄7=441⁄7 |
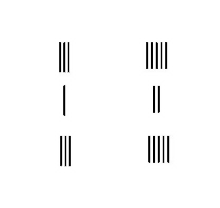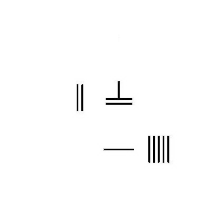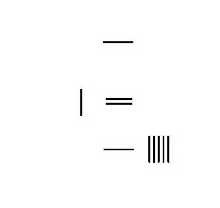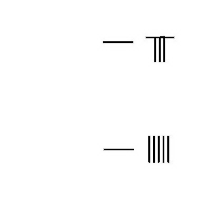 Multiplication de fractions : 31⁄3× 52⁄5=18 |
Racine carrée
Le principe d'extraction de racine carrée est analogue à la méthode d'extraction par l'algorithme de la potence. Si A est le nombre dont on cherche une racine carrée, on cherche d'abord une première approximation x de cette racine. On sait alors que A= (x + d)2= x2 + 2xd + d2. Une approximation y de (A - x2)/(2x) fournit une approximation de d. Le nombre x' = x + y est une nouvelle approximation de √A. On recommence le processus sur x' : on calcule A - x'2 = (A-x2) - (2x + y)y, que l'on divise par 2x' =2x' +2y etc. On trouve ainsi une approximation de √A de plus en plus fine.
Dans la suite x s'écrit nx.10ax et y s'écrit ny.10ay avec ny égal à 0,1,...ou 9
Le calcul avec baguettes prévoit donc
- une ligne pour les approximations successives de √A
- une ligne pour les valeurs successives de A - x2
- une ligne contenant 2x.10ay puis (2x + y).10ay
- une ligne pour placer y.10ay
S'il s'agit de rechercher la racine carrée de 55225[21], on place ce nombre dans la deuxième ligne (ligne du dividende) et à l'aide d'une baguette on détermine l'ordre de grandeur du résultat en déplaçant la baguette de deux cases en deux cases. La baguette se place sous le 5 de gauche. On cherche l'entier dont le carré est le plus proche de 5 : 2 qui fournit la première approximation de la racine x = 200 que l'on place dans la ligne du haut (ligne du quotient) (fig. 1). On enlève 2² à 5 ce qui fournit A - x2 et la ligne 3 sert à placer 2x.10ay, soit 4 que l'on décale d'une case. Il s'agit de diviser 15 par 4, ce qui fournit ny : 3. On place cette valeur dans la ligne 4 décalée d'une case par rapport au chiffre de ligne du dessus (fig. 2). On met dans L3 la somme de L3 et L4, on obtient alors (2x + y)10ay qui, multiplié par ny, donne (2x + y)y (fig.3). On ôte cette valeur à la ligne du dividende pour obtenir A - x'2. On complète alors la ligne du quotient en plaçant ny à droite de l'approximation précédente et on met dans L3 la somme de L2 et L3 ce qui permet d'obtenir (2x+2y)10ay c'est-à-dire 2x'10ax', valeur que l'on décale d'une case (fig. 4). Il reste à continuer le processus en divisant 232 par 46 etc. (fig.5 et 6)
| fig.1 | fig.2 | fig.3 |
| fig.4 | fig.5 | fig.6 |
La racine carrée de A est donc 235
Si le calcul s'arrête à l'unité, c'est que A est un carré parfait, sinon on peut continuer pour trouver une valeur approchée au dixième, au centième ou au millième.
Racine cubique
L'extraction de la racine cubique s'appuie sur le même principe mais nécessite plus de lignes. Si A est le nombre dont on cherche une racine cubique, on cherche d'abord une première approximation x de cette racine. On sait alors que A= (x + d)3= x3 + 3x2d + 3xd2+ d3. Une approximation y de (A - x3)/(3x2) fournit une approximation de d. Le nombre x' = x + y est une nouvelle approximation de la racine cubique de A. On recommence le processus sur x' : on calcule A - x'3 = (A-x3) - (3x2 + 3xy+y2)y, que l'on divise par 3x'2=3x2 + 6xy+3y2etc. On trouve ainsi une approximation de la racine cubique de A de plus en plus fine.
Dans la suite x s'écrit nx.10ax et y s'écrit ny.10ay avec ny égal à 0,1,...ou 9
Le calcul avec baguettes prévoit donc
- une ligne pour les approximations successives de la racine cubique de A
- une ligne pour les valeurs successives de A - x3
- une ligne contenant 3x2.10ay puis (3x2 + 3xy+y2).10ay
- une ligne contenant 3x.102ay puis 3xy.10ay
- une ligne pour placer y2.10ay
S'il s'agit de rechercher la racine cubique de 1860876[22], on place ce nombre dans la deuxième ligne (ligne du dividende) et à l'aide d'une baguette on détermine l'ordre de grandeur du résultat en déplaçant la baguette de trois cases en trois cases. La baguette se place sous le 1 de gauche. On cherche l'entier dont le cube est le plus proche de 1 : 1 qui fournit la première approximation de la racine x = 100 que l'on place dans la ligne du haut (ligne du quotient) (fig. 1). On enlève 13à 1 ce qui fournit A - x3 et la ligne 3 sert à placer 3x2.10ay, soit 3 que l'on décale d'une case. La ligne 4 sert à placer 3x.102ay, soit 3 que l'on décale encore d'une case(fig.2). Il s'agit de diviser 8 par 3, ce qui fournit ny : 2. On multiplie L4 par cette valeur pour obtenir 3xy.10ay et on prend le carré de ny que l'on place dans la ligne 5 décalé encore une fois d'une case , ce qui fournit y2.10ay (fig. 3). On met dans L3 la somme de L3, L4 et L5, on obtient alors (3x2 + 3xy+y2).10ay qui, multiplié par ny, donnera 3x2 + 3xy+y2)y (fig.4). On ote cette valeur à la ligne du dividende pour obtenir A - x'3. On complète alors la ligne du quotient en plaçant ny à droite de l'approximation précédente et on met dans L3 la somme de L3 , L4 et 2L5, ce qui permet d'obtenir (3x2 + 6xy+3y2).10ayc'est-à-dire 3x'2.10ax', valeur que l'on décale d'une case et l'on met dans L4 3x'.102ay, soit 36 (fig. 5). Il reste à continuer le processus en divisant 1328 par 432 etc. (fig.6 , 7, 8)
| fig.1 | fig.2 | fig.3 | fig.4 |
| fig.5 | fig.6 | fig.7 | fig.8 |
La racine cubique de A est donc 123.
Si le calcul s'arrête à l'unité, c'est que A est un cube parfait, sinon on peut continuer pour trouver une valeur approchée au dixième, au centième ou au millième.
Systèmes d'équations
Pour les calculs avec polynômes ou systèmes d'équations linéaires, la surface de calcul s'organise différemment. Dans chaque case, on ne met plus seulement un chiffre constituant un élément de l'écriture décimale d'un nombre, mais on met un nombre (positif ou négatif) représentant un coefficient apparaissant dans le polynôme ou le système d'équations. Les opérations sur les polynômes ou les transformations du système d'équations se résument alors à des manipulations dynamiques de nombres dans un tableau analogue à une matrice.
Le traitement des systèmes d'équations fait l'objet de tout un chapitre FangCheng dans Les Neuf Chapitres sur l'art mathématique et utilise un principe analogue au principe d'élimination de Gauss-Jordan. Ainsi pour résoudre un système que l'on écrit maintenant :
le mathématicien chinois travaille sur un tableau de 3 colonnes et 4 lignes en basculant le système d'un quart de tour dans le sens des aiguilles d'une montre . Il procède ensuite à l'élimination de coefficients par combinaisons linéaires de colonnes jusqu'à n'obtenir qu'un seul coefficient par ligne et par colonne dans le tableau 3 x 3 supérieur[23] ou (Liu din 171-172)
| Placement | 3C2-2C3 en C2 | 3C1-C3 en C1 | |
| (5C1-4C2)/9 en C1 | (4C2-C1)/5 en C2 | (4C3-C1-2C2)/3 en C3 |
Le tableau ainsi diagonalisé fournit x = 37/4 = 91⁄4, y = 17/4 = 41⁄4 et z = 11/4=23⁄4.
Notes et références
- Volkov signale que, dans les sources historiques, la longueur des baguettes est variable de 9 cm à 13,8 cm (Volkov 2001, Bacchette e cosmologia)
- Volkov 2001, I primi riferimenti alle bacchette
- Chemla et Shuchun 2005, p. 15
- Volkov 2001, Bacchette e cosmologia
- Chemla et Shuchun 2005, p. 16
- Volkov 2001, La tavola di calcolo: mito o realtà?
- Chemla et Shuchun 2005, p. 15 note 2
- Commentaires de Liu Hui sur Les neuf chapitres sur l'art mathématique (Volkov 2001, Bacchette e cosmologia)
- Volkov 2001, Dalle bacchette all'abaco
- Liu Dun 1997, p. 170
- Fleeting Footsteps, p. 79
- Liu Dun 1997, p. 166
- Liu Dun 1997, p. 167
- Dauben 2007, p. 324
- Volkov 2001, Il sistema di numerazione cinese, sistema decimale e principio posizionale
- Fleeting Footsteps, p. 83-84
- Volkov 2001, Rappresentazione dei numeri e operazioni calcul
- Chemla et Shuchun 2005, p. 16-19
- Fleeting Footsteps, p. 88
- Chemla et Shuchun 2005, p. 133
- Chemla et Shuchun 2005, p. 322-326
- Chemla et Shuchun 2005, p. 371-375
- Chemla et Shuchun 2005, p. 602-604
Bibliographie
- Karine Chemla et Guo Shuchun, Les neuf chapitres : Le classique mathématique de la Chine ancienne et ses commentaires [détail de l’édition]
- (en) Joseph W. Dauben, « Chinese mathematics », dans The mathematics of Egypt, Mesopotamia, China, India, and Islam : A Sourcebook, Princeton university press, , p. 187-384
- (it) Alexei Volkov, « La scienza in Cina: dai Qin-Han ai Tang. La matematica : Le bacchette », dans Collectif, Storia della Scienza, (lire en ligne).
- Liu Dun, « Nombres, outils de calcul et expressions mathématiques en Chine ancienne », dans Collectif, L’océan Indien au carrefour des mathématiques arabes, chinoises, européennes et indiennes : Saint-Denis de la Réunion, 3-7 novembre 1997, actes du colloque, IUFM de La Réunion, (lire en ligne), p. 161-177
- André Bréard, Le calcul à baguettes en Chine ancienne, université de Lille-1
- (en) Lay Yon Lam et Tian Se Ang, Fleeting Footsteps : Tracing the Conception of Arithmetic and Algebra in Ancient China, World Scientific Pub Co Inc, 2004 (revised edition) (présentation en ligne)




















