Arbre de Calkin-Wilf
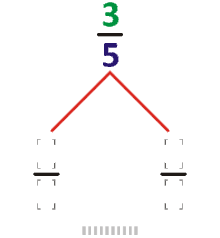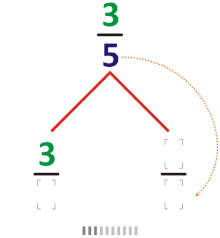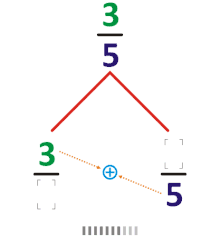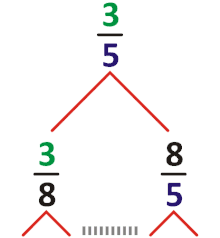
En théorie des nombres et en combinatoire, l'arbre de Calkin-Wilf, est un arbre dont les sommets sont en bijection avec les nombres rationnels positifs. L'arbre a pour racine le nombre 1, et tout nombre rationnel positif, exprimé sous la forme d'une fraction réduite a/b, a deux enfants qui correspondent aux nombres a/(a + b) et (a + b)/b. Chaque nombre rationnel positif figure exactement une fois dans l’arbre.
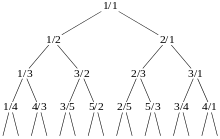
La suite de nombres rationnels obtenue par un parcours en largeur de l'arbre de Calkin-Wilf est connue sous le nom de suite de Calkin-Wilf. La suite des numérateurs (ou la suite des dénominateurs décalée d'un terme) est la suite diatomique de Stern, et peut être calculée par la fonction fusc.
Historique

L'arbre de Calkin-Wilf porte le nom de Neil Calkin (en) et Herbert Wilf qui l'ont étudié dans un article commun paru en 2000. L'arbre a été introduit auparavant par Jean Berstel et Aldo de Luca[1] sous le nom de Raney tree, parce qu'ils ont repris des concepts d'un article de George N. Raney[2]. La suite diatomique de Stern a été décrite bien plus tôt par Moritz Abraham Stern, mathématicien allemand du XIXe siècle qui est aussi l'inventeur de l'arbre de Stern-Brocot.
Et même encore plus tôt, un arbre semblable (incluant seulement les fractions entre 0 et 1) apparaît chez Johannes Kepler dans son Harmonices Mundi (1619)[3].
Définition et structure
On peut définir l’arbre de Calkin-Wilf comme étant un graphe orienté, où chaque nombre rationnel positif figure comme sommet et possède, à l'exception du sommet 1, un arc sortant unique vers un autre sommet appelé son sommet parent. On suppose que la fraction est réduite, en d'autres termes que le plus grand commun diviseur de a et b est 1. Si , le parent de est ; si , le parent de est . Dans les deux cas, le parent est une fraction dont la somme du numérateur et du dénominateur est plus petite; de sorte que la répétition de ces réductions amène finalement au nombre 1, sans parent, la racine. Il s'agit bien d'un arbre au sens de la théorie des graphes, avec un seul arc sortant par sommet et une racine accessible de tout sommet.
Les enfants d'un sommet de l'arbre de Calkin-Wilf se calculent en inversant les formules précédentes : chaque sommet a/b a un enfant de valeur plus petite que 1, et un enfant de valeur plus grande que 1[4]. L'arbre de Calkin-Wilf est bien un arbre binaire, mais sans être un arbre binaire de recherche, car l'ordre obtenu par le parcours infixe ne correspond pas à l'ordre naturel des sommets. Il existe toutefois une relation étroite avec l'arbre de Stern-Brocot (qui est lui un arbre binaire de recherche) : les sommets des deux arbres sont les mêmes à chaque niveau, et ils sont liés par la permutation obtenue en renversant la représentation binaire de leur position, appelée en anglais la bit-reversal permutation (en)[5].
Parcours en largeur
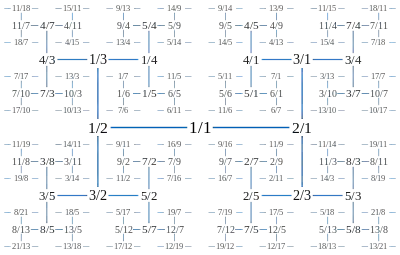
La suite de Calkin–Wilf est la suite de nombres rationnels obtenue par un parcours en largeur de l'arbre de Calkin-Wilf. Ses premiers éléments sont :
- 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4, 4/3, 3/5, 5/2, 2/5, 5/3, 3/4, ...
Comme l'arbre de Calkin-Wilf contient chaque nombre rationnel positif exactement une fois, il en est de même de cette suite. Le dénominateur de chaque fraction est égal au numérateur de la fraction suivante[6]. La suite peut aussi être engendrée par la formule de récurrence :
où est le i-ème nombre de la suite, avec , et est la partie entière de [7].
On peut aussi calculer directement à partir du run-length encoding de la représentation binaire de i : on compte le nombre de chiffres égaux à 1 à partir du bit de plus faible poids, puis le nombre de chiffres égaux à 0, puis à nouveau le nombre de chiffres égaux à 1 etc. La suite d'entiers positifs ainsi obtenue est la représentation en fraction continue de .
- Exemples
- pour , la fraction continue obtenue est [1;2,3,4,1], et donc .
- pour , la fraction continue est [0;1,2,3,5], et
- Attention, la réciproque n'est pas toujours vraie, une fraction continue peut avoir une valeur binaire identique à une autre.
- les fractions continues de et de sont respectivement [0, 2] et [1, 2], donc et . Pour retrouver la position d'un nombre il faut absolument remonter vers la racine de l'arbre en ajoutant si le numérateur est supérieur au dénominateur 1 à l'avant du résultat binaire et 0 sinon.
var p = parseInt(n); // numérateur var q = parseInt(d); // dénominateur var bits = ""; while (!(p == 1 && q == 1)) { // tant qu'on est pas à la racine if (p > q) { bits = "1" + bits; p = p - q; } else { bits = "0" + bits; q = q - p; } } bits = "1" + bits; // le bit de la racine var resultat = parseInt(bits, 2);
Une conversion similaire entre développements binaires codés en run-length encoding et fractions continues peut être utilisée pour évaluer la fonction point d'interrogation de Minkowski ; dans l'arbre de Calkin–Wilf, les nombres binaires sont des entiers, à savoir les positions dans le parcours en largeur, alors que dans la fonction point d'interrogation ce sont des nombres réels entre 0 et 1.
Suite diatomique de Stern
La suite diatomique de Stern est la suite d'entiers
Si on numérote les éléments à partir de 0, la valeur du n-ième de la suite est la valeur fusc(n) de la fonction fusc[8], fonction définie par la relation de récurrence
avec les conditions initiales
- et .
Le n-ième nombre dans le parcours en profondeur de l'arbre de Calkin–Wilf est le nombre [9]. Ceci montre que la suite diatomique forme à la fois la suite des numérateurs et la suite des dénominateurs des nombres de la suite de Calkin–Wilf.
Le nombre fusc(n + 1) est aussi le nombre de coefficients binomiaux impairs de la forme[10]
et il compte également le nombre de façons d'écrire n comme une somme de puissances de deux où chaque puissance apparaît au plus deux fois. On peut voir cela à partir de la relation de récurrence qui définit fusc comme suit : les expressions comme somme de puissances de 2 pour un nombre pair 2n ou bien ne comportent pas de 1, (et dans ce cas elles sont formées en doublant chaque terme de l'expression pour n) ou bien comportent deux 1 (et dans ce cas le reste de l'expression est formé en doublant chaque terme de l'expression pour n - 1), de sorte que le nombre de représentants est la somme du nombre de représentations pour n et pour n - 1, en accord avec la relation de récurrence. De même, chaque représentation pour un nombre impair 2n + 1 est formé en doublant une représentation pour n et en ajoutant 1, à nouveau en accord avec la récurrence[11]. Par exemple
- 6 = 4 + 2 = 4 + 1 + 1 = 2 + 2 + 1 + 1
a trois représentations comme somme de puissances de deux ayant au plus deux occurrences de chaque puissance, de sorte que fusc(6 + 1) = 3.
Rapport avec l'arbre de Stern–Brocot
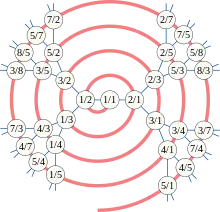
L'arbre de Calkin–Wilf ressemble à l'arbre de Stern-Brocot, dans la mesure où les deux sont des arbres binaires contenant chaque nombre rationnel positif exactement une fois. De plus, les mêmes nombres apparaissent dans les deux arbres aux mêmes niveaux, mais pas dans le même ordre. Les arbres peuvent être obtenus l'un à partir de l’autre au moyen d'une bit-reversal permutation (en)[12] appliquée à chaque niveau de l'arbre[5]. On peut aussi transformer le nombre associé à un nœud donné de l'arbre de Calkin–Wilf en le nombre en même position dans l'arbre de Stern–Brocot et réciproquement par une méthode qui utilise le retournement de la représentation en fraction continue de ces nombres[13]. Les deux arbres ont aussi des propriétés qui les distinguent : un arbre de Stern–Brocot est un arbre binaire de recherche, c'est-à-dire que le parcours infixe de gauche à droite donne les nombres en ordre numérique croissant, alors que l'arbre de Calkin–Wilf n'a pas cette propriété.
Notes et références
- Berstel et de Luca 1997, Section 6.
- Raney 1973.
- J. Kepler, Harmonices Mundi, vol. III, (lire en ligne), p. 27.
- La description donnée ici est duale de la définition de Calkin et Wilf ; ces auteurs commencent par la définition des enfants à partir de leur parent et déduisent ensuite les expressions pour le parent.
- Gibbons, Lester et Bird 2006.
- Gibbons, Lester et Bird 2006 discutent des techniques de programmation fonctionnelle pour réaliser ce parcours en largeur.
- Aigner et Ziegler 2004 attribuent cette formule à Moshe Newman.
- Le nom « fusc » a été donné à cette fonction en 1976 par Edsger W. Dijkstra, comme indiqué dans EWD570 et EWD578.
- Calkin et Wilf 2000, Theorem 1.
- Carlitz 1964.
- L'entrée de OEIS attribue ce fait à Carlitz 1964 et à un papier non cité de Lind. L'article de Carlitz décrit en fait une classe plus restreinte de sommes de puissances de 2, comptées par la fonction fusc(n) au liu de fusc(n + 1).
- Les indices d'un mot abcdefgh à huit lettres s'écrivent, en binaire, 000, 001, 010, 011, 100, 101, 110, et 111; les écritures renversées deviennent 000, 100, 010, 110, 001, 101, 011, et 111. La séquence permutée est aecgbfdh.
- et al. 2010.
Bibliographie
- Martin Aigner et Günter M. Ziegler, Proofs from THE BOOK, Berlin; New York, Springer, , 3e éd., 239 p. (ISBN 978-3-540-40460-6), p. 94–97
- Martin Aigner et Günter M. Ziegler, Raisonnements divins, Paris ; Berlin, Springer, , 3e éd., 308 p. (ISBN 978-2-8178-0399-9), p. 121-122
- Bruce Bates, Martin Bunder et Keith Tognetti, « Linking the Calkin-Wilf and Stern-Brocot trees », European Journal of Combinatorics, vol. 31, no 7, , p. 1637–1661 (DOI 10.1016/j.ejc.2010.04.002, MR 2673006)
- Jean Berstel et Aldo de Luca, « Sturmian words, Lyndon words and trees », Theoretical Computer Science, vol. 178, , p. 171–203 (DOI 10.1016/S0304-3975(96)00101-6)
- Neil Calkin et Herbert Wilf, « Recounting the rationals », American Mathematical Monthly, Mathematical Association of America, vol. 107, no 4, , p. 360–363 (DOI 10.2307/2589182, JSTOR 2589182, lire en ligne).
- Leonard Carlitz, « A problem in partitions related to the Stirling numbers », Bulletin of the American Mathematical Society, vol. 70, no 2, , p. 275–278 (DOI 10.1090/S0002-9904-1964-11118-6, MR 0157907).
- Edsger W. Dijkstra, Selected Writings on Computing : A Personal Perspective, Springer-Verlag, (ISBN 978-0-387-90652-2). — (EWD 570: An exercise for Dr.R.M.Burstall, p. 215–216, et EWD 578: More about the function "fusc" (A sequel to EWD570), pp. 230–232 ; réimpressions de notes écrites en 1976.)
- Jeremy Gibbons, David Lester et Richard Bird, « Functional pearl: Enumerating the rationals », Journal of Functional Programming, vol. 16, no 3, , p. 281–291 (DOI 10.1017/S0956796806005880).
- George N. Raney, « On continued fractions and finite automata », Mathematische Annalen, vol. 206, , p. 265–283 (DOI 10.1007/BF01355980)
- Moritz A. Stern, « Ueber eine zahlentheoretische Funktion », Journal für die reine und angewandte Mathematik, vol. 55, , p. 193–220 (lire en ligne).
Articles liés
Liens externes
- (en) Eric W. Weisstein, « Calkin–Wilf Tree », sur MathWorld
- (en) Eric W. Weisstein, « Stern's Diatomic Series », sur MathWorld
- Alexander Bogomolny, « Fractions on a Binary Tree II », Cut-the-knot
























