Analogie de Maxwell
L'analogie d'impédance ou analogie de Maxwell est une méthode de représentation d'un système mécanique par un système électrique analogue. L'avantage de celle-ci est qu'il existe un grand nombre de théories et de techniques d'analyse concernant les systèmes électriques complexes, en particulier dans le domaine des filtres[1]. En convertissant vers une représentation électrique, ces outils du domaine électrique peuvent être directement appliqués à un système mécanique sans modification. Un autre avantage apparaît dans les systèmes électromécaniques : la conversion de la partie mécanique d'un tel système dans le domaine électrique permet d'analyser l'ensemble du système comme un tout unifié.
Le comportement mathématique du système électrique simulé est identique au comportement mathématique du système mécanique représenté. À chaque élément du domaine électrique correspond un élément du domaine mécanique avec une équation de comportement analogue. Toutes les lois d'analyse de circuit, telles que les lois de circuit de Kirchhoff, qui s'appliquent dans le domaine électrique s'appliquent également à l'analogie de l'impédance mécanique.
L'analogie d'impédance est l'une des deux principales analogies mécaniques-électriques utilisées pour représenter les systèmes mécaniques dans le domaine électrique, l'autre étant l'analogie de mobilité . Les rôles de la tension et du courant sont inversés dans ces deux méthodes, et les représentations électriques produites sont les doubles circuits l'un de l'autre. L'analogie de l'impédance préserve l'analogie entre l'impédance électrique et l'impédance mécanique alors que l'analogie de la mobilité ne le fait pas. D'autre part, l'analogie de la mobilité préserve la topologie du système mécanique lorsqu'elle est transférée au domaine électrique alors que l'analogie de l'impédance ne le fait pas.
Applications
L'analogie d'impédance est largement utilisée pour modéliser le comportement des filtres mécaniques. Ce sont des filtres destinés à être utilisés dans un circuit électronique, mais qui fonctionnent entièrement par ondes vibratoires mécaniques. Des transducteurs sont prévus à l'entrée et à la sortie du filtre pour effectuer la conversion entre les domaines électrique et mécanique[2].
Une autre utilisation très courante se situe dans le domaine des équipements audio, tels que les haut-parleurs. Ces derniers se composent d'un transducteur et de pièces mobiles mécaniques. Les ondes acoustiques elles-mêmes sont des ondes de mouvement mécanique : de molécules d'air ou d'un autre milieu fluide. Une des premières applications de ce type consistait à apporter des améliorations significatives aux performances audio abyssales des phonographes. En 1929, Edward Norton a conçu les parties mécaniques d'un phonographe pour qu'elles se comportent comme un filtre plat au maximum, anticipant ainsi le filtre électronique de Butterworth.
Éléments
Avant qu'une analogie électrique puisse être développée pour un système mécanique, il doit d'abord être décrit comme un réseau mécanique abstrait. Le système mécanique est décomposé en un certain nombre d'éléments idéaux dont chacun peut ensuite être associé à un analogue électrique[3]. Les symboles utilisés pour ces éléments mécaniques sur les schémas de réseau sont indiqués dans les sections suivantes sur chaque élément individuel.
Les analogies mécaniques des éléments électriques localisés sont également des éléments localisés, c'est-à-dire que l'on suppose que le composant mécanique possédant l'élément est suffisamment petit pour que le temps mis par les ondes mécaniques pour se propager d'une extrémité du composant à l'autre puisse être négligé. Des analogies peuvent également être développées pour les éléments distribués tels que les lignes de transmission, mais les plus grands avantages sont avec les circuits à éléments localisés. Des analogies mécaniques sont requises pour les trois éléments électriques passifs, à savoir la résistance, l'inductance et la capacité. Ces analogies sont déterminées par la propriété mécanique choisie pour représenter "l'effort", l'analogie de la tension, et la propriété choisie pour représenter le "débit", l'analogie du courant[4]. Dans l'analogie de l'impédance, la variable d'effort est la force et la variable de débit est la vitesse[5] .
Résistance
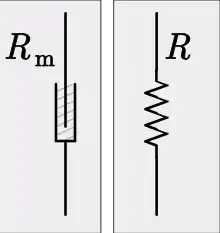
L'analogie mécanique de la résistance électrique est la perte d'énergie d'un système en mouvement par des processus tels que le frottement. Un composant mécanique analogue à une résistance est un amortisseur et la propriété analogue à la résistance est l'amortissement. Une résistance est régie par l'équation constitutive de la loi d' Ohm,
L'équation analogue dans le domaine mécanique est :
où
- R est la résistance
- v est la tension
- i est l'intensité
- Rm est la résistance mécanique
- F est la force
- u est la célérité induite par la force
La résistance électrique représente la partie réelle de l'impédance électrique . De même, la résistance mécanique est la partie réelle de l'impédance mécanique[7] .
Inductance
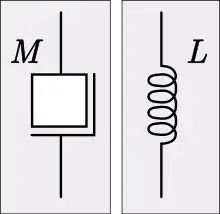
L'analogue mécanique de l'inductance dans l'analogie de l'impédance est la masse. Un composant mécanique analogue à un inducteur est un gros poids rigide. Une inductance est régie par l'équation constitutive,
L'équation analogue dans le domaine mécanique est la deuxième loi du mouvement de Newton :
où
- L est l'inductance
- t est le temps
- M est la masse[5]
L'impédance d'une inductance est purement imaginaire et est donnée par
L'impédance mécanique analogue est donnée par
où
- Z est l'impédance électrique
- j est l'unité imaginaire ;
- ω est la fréquence angulaire ;
- Zm est l'impédance mécanique[9].
Capacitance
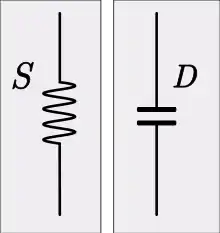
L'analogie mécanique de la capacité dans l'analogie de l'impédance est la conformité. Il est plus courant en mécanique de parler de raideur, l'inverse de la souplesse. L'analogie de la rigidité dans le domaine électrique est l'élastance moins couramment utilisée, l'inverse de la capacité [11]. Un composant mécanique analogue à un condensateur est un ressort[10]. Un condensateur est régi par l'équation constitutive,
L'équation analogue dans le domaine mécanique est une forme de la loi de Hooke ,
où
- D = 1/C est l'élastance
- C est la capacitance
- S est la raideur.
L'impédance d'un condensateur est purement imaginaire et est donnée par,
L'impédance mécanique analogue est donnée par
Alternativement, on peut écrire
où est la conformité mécanique. Ceci est plus directement analogue à l'expression électrique lorsque la capacité est utilisée[12].
Résonateur
Un résonateur mécanique se compose à la fois d'un élément de masse et d'un élément de souplesse. Les résonateurs mécaniques sont analogues aux circuits électriques LC constitués d'une inductance et d'une capacité. Les composants mécaniques réels ont inévitablement à la fois une masse et une souplesse, il est donc pratique de fabriquer des résonateurs en un seul composant. En fait, il est plus difficile de fabriquer une pure masse ou une pure souplesse en un seul composant. Un ressort peut être fabriqué avec une certaine souplesse et une masse minimisée, ou une masse peut être fabriquée avec une souplesse minimisée, mais aucune ne peut être complètement éliminée. Les résonateurs mécaniques sont un élément clé des filtres mécaniques[13].
Générateurs
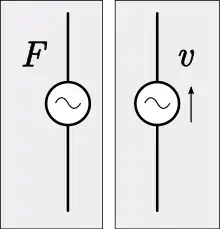
Des analogues existent pour les éléments électriques actifs de la source de tension et de la source de courant (générateurs). L'analogue mécanique dans l'analogie d'impédance du générateur de tension constante est le générateur de force constante. L'analogue mécanique du générateur de courant constant est le générateur de vitesse constante[14].
Un exemple de générateur de force constante est le ressort à force constante. Ceci est analogue à une source de tension réelle, telle qu'une batterie, qui reste proche de la tension constante avec charge à condition que la résistance de charge soit bien supérieure à la résistance interne de la batterie. Un exemple de générateur pratique à vitesse constante est une machine puissante légèrement chargée, telle qu'un moteur, entraînant une courroie[15].
Transducteurs
Les systèmes électromécaniques nécessitent des transducteurs pour effectuer la conversion entre les domaines électrique et mécanique. Ils sont analogues aux réseaux à deux ports et, comme ceux-ci, peuvent être décrits par un système de deux équations à quatre paramètres arbitraires, couplées. Il existe de nombreuses représentations possibles, mais la forme la plus applicable à l'analogie de l'impédance a les paramètres arbitraires en unités d'impédance. Sous forme matricielle (avec le côté électrique pris comme port 1), cette représentation est
L'élément z22 est l'impédance mécanique en circuit ouvert, c'est-à-dire l'impédance présentée par le côté mécanique du transducteur lorsqu'aucun courant (circuit ouvert) n'entre dans le côté électrique. L'élément z11, à l'inverse, est l'impédance électrique bloquée, c'est-à-dire l'impédance présentée au côté électrique lorsque le côté mécanique est bloqué et empêché de se déplacer (la vitesse est nulle). Les deux éléments restants, z21 et z12, décrivent respectivement les fonctions de transfert direct et inverse du transducteur. Ils sont tous deux analogues aux impédances de transfert et sont des rapports hybrides d'une grandeur électrique et mécanique.
Transformateurs
L'analogie mécanique d'un transformateur est une machine simple telle qu'une poulie ou un levier. La force appliquée à la charge peut être supérieure ou inférieure à la force d'entrée selon que l'avantage mécanique de la machine est respectivement supérieur ou inférieur à l'unité. L'avantage mécanique est analogue au rapport de transformation du transformateur dans l'analogie de l'impédance. Un avantage mécanique supérieur à l'unité est analogue à un transformateur élévateur et inférieur à l'unité est analogue à un transformateur abaisseur.
Équations de puissance et d'énergie
| Quantité électrique | Expression électrique | Analogie mécanique | Expression mécanique |
|---|---|---|---|
| Énergie fournie | Énergie fournie | ||
| Alimentation fournie | Alimentation fournie | ||
| Dissipation de puissance dans une résistance | Dissipation de puissance dans un registre [6] | ||
| Énergie stockée dans un champ magnétique inducteur | Énergie cinétique d'une masse en mouvement [1] | ||
| Énergie stockée dans un champ électrique de condensateur | Énergie potentielle stockée dans un ressort [1] |
Exemples
Circuit résonant simple
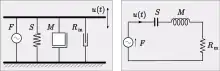
La figure montre un agencement mécanique d'une plate-forme de masse qui est suspendu au-dessus du substrat par un ressort de raideur et un amortisseur de résistance Le circuit équivalent d'analogie d'impédance est représenté à droite de cet arrangement et se compose d'un circuit résonnant en série. Ce système a une fréquence de résonance, et peut avoir une fréquence naturelle d'oscillation s'il n'est pas trop fortement amorti[16].
Modèle de l'oreille humaine

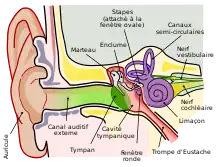
Le schéma de circuit montre un modèle d'analogie d'impédance de l'oreille humaine. La section du conduit auditif est suivie d'un transformateur représentant le tympan. Le tympan est le transducteur entre les ondes acoustiques dans l'air du conduit auditif et les vibrations mécaniques dans les os de l'oreille moyenne. Au niveau de la cochlée, il y a un autre changement de milieu des vibrations mécaniques au fluide remplissant la cochlée. Cet exemple démontre ainsi la puissance des analogies électriques pour réunir trois domaines (acoustique, mécanique et fluidique) en un seul ensemble unifié. Si les impulsions nerveuses circulant vers le cerveau avaient également été incluses dans le modèle, le domaine électrique aurait fait quatre domaines englobés dans le modèle.
La partie cochléaire du circuit utilise une analyse par éléments finis de la ligne de transmission continue du conduit cochléaire. Une représentation idéale d'une telle structure utiliserait des éléments infinitésimaux, et il y en aurait donc un nombre infini. Dans ce modèle, la cochlée est divisée en 350 sections et chaque section est modélisée à l'aide d'un petit nombre d'éléments groupés[17].
Avantages et inconvénients
Le principal avantage de l'analogie d'impédance par rapport à son alternative, l'analogie de mobilité, est qu'elle maintient l'analogie entre l'impédance électrique et mécanique. C'est-à-dire qu'une impédance mécanique est représentée comme une impédance électrique et une résistance mécanique est représentée comme une résistance électrique dans le circuit électrique équivalent. Il est également naturel de considérer la force comme analogue à la tension (les tensions du générateur sont souvent appelées force électromotrice) et la vitesse comme analogue au courant. C'est cette analogie de base qui conduit à l'analogie entre l'impédance électrique et mécanique[4].
Le principal inconvénient de l'analogie d'impédance est qu'elle ne préserve pas la topologie du système mécanique. Les éléments qui sont en série dans le système mécanique sont en parallèle dans le circuit électrique équivalent et vice versa .
La représentation matricielle de l'impédance d'un transducteur transforme la force dans le domaine mécanique en courant dans le domaine électrique. De même, la vitesse dans le domaine mécanique est transformée en tension dans le domaine électrique. Un dispositif à deux ports qui transforme une tension en une grandeur analogue peut être représenté comme un simple transformateur. Un dispositif qui transforme une tension en un analogue de la double propriété de la tension (c'est-à-dire le courant, dont l'analogue est la vitesse) est représenté par un gyrateur[18]. Étant donné que la force est analogue à la tension et non au courant, cela peut sembler un inconvénient à première vue. Cependant, de nombreux transducteurs pratiques, en particulier aux fréquences audio, fonctionnent par induction électromagnétique et sont régis par une telle relation[19]. Par exemple, la force sur un conducteur sous tension est donnée par,
où
- B est la densité de flux magnétique
- l est la longueur du conducteur.
Histoire
L'analogie de l'impédance est appelée l'analogie de Maxwell [4] d'après James Clerk Maxwell (1831–1879) qui a utilisé des analogies mécaniques pour expliquer ses idées sur les champs électromagnétiques[20]. Cependant, le terme impédance n'a été inventé qu'en 1886 (par Oliver Heaviside [21]), l'idée d' impédance complexe a été introduite par Arthur E. Kennelly en 1893, et le concept d'impédance n'a été étendu au domaine mécanique qu'en 1920 par Kennelly et Arthur Gordon Webster[22].
Henri Poincaré en 1907 a été le premier à décrire un transducteur comme une paire d'équations algébriques linéaires reliant des variables électriques (tension et courant) à des variables mécaniques (force et vitesse)[23]. Wegel, en 1921, a été le premier à exprimer ces équations en termes d'impédance mécanique ainsi que d'impédance électrique.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Impedance analogy » (voir la liste des auteurs).
- Talbot-Smith, p. 1.86
- Carr, pp. 170–171
- Kleiner, pp. 69–70
- Busch-Vishniac, p. 20
- Talbot-Smith, pp. 1.85–1.86
- Eargle, p. 4
- Kleiner, p. 71
- Kleiner, p. 74
- Kleiner, pp. 73–74
- Kleiner, p. 73
- Pipes & Harvill, p. 187
- Kleiner, pp. 72–73
- Taylor & Huang, pp. 377–383
- Kleiner, pp. 76–77
- Kleiner, p. 77
- Eargle, pp. 3–4
- Fukazawa & Tanaka, pp. 191–192
- Beranek & Mellow, pp. 70–71
- Eargle, pp. 5–7
- Stephens & Bate, p. 421
- Martinsen & Grimnes, p. 287
- Hunt p. 66
- Pierce, p. 200, cites Poincaré
Bibliographie
- Beranek, Leo Leroy; Mellow, Tim J., Acoustics: Sound Fields and Transducers, Academic Press, 2012 (ISBN 0123914213).
- Busch-Vishniac, Ilene J., Electromechanical Sensors and Actuators, Springer Science & Business Media, 1999 (ISBN 038798495X).
- Carr, Joseph J., RF Components and Circuits, Newnes, 2002 (ISBN 0-7506-4844-9).
- Darlington, S. "A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors", IEEE Transactions on Circuits and Systems, vol. 31, no. 1, pp. 3–13, 1984.
- Eargle, John, Loudspeaker Handbook, Kluwer Academic Publishers, 2003 (ISBN 1402075847).
- Fukazawa, Tatsuya; Tanaka, Yasuo, "Evoked otoacoustic emissions in a cochlear model", pp. 191–196 in Hohmann, D. (ed), ECoG, OAE and Intraoperative Monitoring: Proceedings of the First International Conference, Würzburg, Germany, September 20–24, 1992, Kugler Publications, 1993 (ISBN 9062990975).
- Harrison, Henry C. "Acoustic device", (en) Brevet U.S. 1730425, filed 11 October 1927 (and in Germany 21 October 1923), issued 8 October 1929.
- Hunt, Frederick V., Electroacoustics: the Analysis of Transduction, and its Historical Background, Harvard University Press, 1954 (OCLC 2042530).
- Jackson, Roger G., Novel Sensors and Sensing, CRC Press, 2004 (ISBN 1420033808).
- Kleiner, Mendel, Electroacoustics, CRC Press, 2013 (ISBN 1439836183).
- Martinsen, Orjan G.; Grimnes, Sverre, Bioimpedance and Bioelectricity Basics, Academic Press, 2011 (ISBN 0080568807).
- Paik, H. J., "Superconduction accelerometers, gravitational-wave transducers, and gravity gradiometers", pp. 569–598, in Weinstock, Harold, SQUID Sensors: Fundamentals, Fabrication, and Applications, Springer Science & Business Media, 1996 (ISBN 0792343506).
- Pierce, Allan D., Acoustics: an Introduction to its Physical Principles and Applications, Acoustical Society of America 1989 (ISBN 0883186128).
- Pipes, Louis A.; Harvill, Lawrence R., Applied Mathematics for Engineers and Physicists, Courier Dover Publications, 2014 (ISBN 0486779513).
- Poincaré, H., "Study of telephonic reception", Eclairage Electrique, vol. 50, pp. 221–372, 1907.
- Stephens, Raymond William Barrow; Bate, A. E., Acoustics and vibrational physics, Edward Arnold, 1966 (OCLC 912579).
- Talbot-Smith, Michael, Audio Engineer's Reference Book, Taylor & Francis, 2013 (ISBN 1136119736).
- Taylor, John; Huang, Qiuting, CRC Handbook of Electrical Filters, CRC Press, 1997 (ISBN 0849389518).
- Wegel, R. L., "Theory of magneto-mechanical systems as applied to telephone receivers and similar structures", Journal of the American Institute of Electrical Engineers, vol. 40, pp. 791–802, 1921.