Énergie d'activation
L'énergie d'activation est une notion introduite en 1889 par le scientifique suédois Svante August Arrhenius, après avoir constaté la loi empirique qui porte son nom et qui décrit l’évolution d’une vitesse de réaction chimique avec la température. Dans sa loi (voir ci-dessous), il apparaît un terme qui possède la dimension d’une énergie molaire et qu’il appelle énergie d’activation[1].

Le sens intuitif qui peut être donné à cette notion est celui d'une énergie qui doit être apportée à un système chimique pour que la réaction ait lieu. Cette énergie est de nature thermique.
Le sens théorique qui peut être donné à cette notion se réfère à l’équation d'Eyring qui découle d’un cadre théorique (et non de mesures empiriques). Dans la théorie d’Eyring (appelée théorie du complexe activé), l’énergie d’activation est l’enthalpie libre qui sépare l’énergie de l’état de transition et celle de l’état initial.
Cette énergie d'activation peut être diminuée, en utilisant un catalyseur.
Loi d'Arrhenius et énergie d'activation
L'expression de la loi d'Arrhenius fait apparaître l'énergie d'activation :
avec :
- la constante de vitesse de la réaction (quand elle existe) ;
- le facteur préexponentiel auquel Arrhenius ne donne pas de signification, appelé facteur de fréquence ;
- (ou bien Ea) l'énergie d'activation en J·mol−1 ;
- la constante universelle des gaz parfaits (8,31 J·mol−1 ·K−1) ;
- la température en kelvins.
Détermination de l'énergie d'activation
Approche expérimentale
Pour déterminer une énergie d'activation, il est nécessaire de déterminer la vitesse de la réaction en fonction de la température.
À partir des mesures à deux températures, le rapport des vitesses de réaction (donc des constantes de vitesses) fait disparaître le facteur préexponentiel et donne accès à . L'énergie d'activation est alors donnée par la relation
Il est plus précis de déterminer la vitesse à plusieurs températures et de faire un graphique de en fonction de . Selon la loi d'Arrhenius ce graphique est une droite de pente , alors [2].
Les valeurs trouvées sont normalement positives et correspondent aux barrières énergétiques que le système doit franchir en allant des réactifs aux produits. Dans ce cas il y a augmentation de vitesse en fonction de température. Il y a cependant des réactions exceptionnelles qui ont des énergies d'activation zéro ou bien négatives.
L'énergie d'activation est zéro si la vitesse est constante en fonction de température, ce qui indique l'absence d'une barrière. Un exemple est la recombinaison de deux radicaux méthyle pour former l'éthane : 2 CH3 → C2H6[2]. Cette réaction correspond à la formation d'une nouvelle liaison C-C sans briser aucune liaison.
L'énergie d'activation est négative au cas d'une réaction dont la vitesse diminue quand la température augmente. Ceci peut avoir lieu pour différentes raisons indiquées ci-dessous
Approche théorique
Lors de réactions par transferts d'électrons, la théorie de Marcus permet de déterminer théoriquement l'énergie d'activation. Le transfert d'électron intervient en effet dans le complexe activé à l'intersection des deux surfaces d'énergie potentielle qui décrivent l'état initial et l'état final. L'énergie d'activation est alors reliée à l'énergie de la réaction par une relation quadratique :
où est un paramètre de réorganisation qui a les dimensions d'une énergie[3].
Conséquences
Règle pratique sur la diminution de la durée d'une réaction
Une règle pratique, en solution, est de considérer que la durée d'une réaction est diminuée de moitié quand la température est augmentée de 10 °C[4]. Cette règle se comprend à l'aide de la loi d'Arrhenius et n'est en fait correcte que pour une certaine valeur de l'énergie d'activation qui se détermine ainsi :
car , soit :
à 316 K.
Cela correspond effectivement à une énergie d'activation et à une température habituelles en chimie organique.
Équilibre chimique
Pour un équilibre chimique, les énergies d'activation de la réaction directe et de la réaction inverse ne sont égales que si la réaction globale est athermique (). Dans le cas d'une réaction exothermique (), l'énergie d'activation de la réaction inverse est plus grande que celle de la réaction directe, et inversement pour une réaction endothermique ().
Catalyseurs
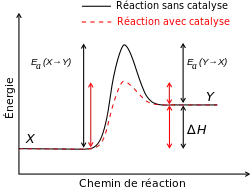
Une substance qui modifie l'état de transition pour baisser l'énergie d'activation est dit un catalyseur. Un catalyseur composé seulement d'une protéine et possiblement des petites molécules comme cofacteurs est dit une enzyme. Un catalyseur augmente la vitesse de réaction sans être consommé dans la réaction[5]. Le catalyseur diminue l'énergie d'activation, mais il ne change pas les énergies des réactifs et des produits, et alors ne change pas l'état d'équilibre[6].
Un catalyseur peut réduire l'énergie d'activation en formant l'état de transition de façon plus favorable lorsqu'un réactif se lie au site actif du catalyseur. Il peut se lier par divers types de force intermoléculaire: liaison hydrogène, force de van der Waals etc. Ces forces stabilisent l'état de transition de la réaction catalysée et alors diminuent l'énergie d'activation.
Énergie d'activation négative
Dans certains cas, la vitesse de réaction diminue en fonction de la température. Si la variation est approximativement exponentielle, la constante de vitesse peut quand même être décrite par la loi d'Arrhenius avec une valeur négative de .
Les réactions élémentaires qui montrent des énergies d'activation négatives sont typiquement des réactions sans barrière, dont la progression dépend de la capture des molécules dans un puits de potentiel. Augmenter la température conduit à une probabilité réduite que la collision de deux molécules devienne la capture de l'une par l'autre, de sorte que la section efficace pour la réaction diminue. Les collisions moins directes ne donnent pas de réaction parce que l'impulsion plus élevée sort les particules en collision du puits de potentiel. Une telle situation ne conduit plus à l'interprétation directe comme la hauteur d'une barrière de potentiel[7].
Des réactions à plusieurs étapes peuvent aussi avoir des énergies d'activation négatives apparentes. Un exemple peut être une réaction à deux étapes où la première étape est un pré-équilibre rapide et la deuxième étape est lente et cinétiquement déterminante : et . La constante de vitesse globale est donnée par k = k2K1, où k2 est la constante de vitesse de la deuxième étape et K1 est la constante d'équilibre de la première étape rapide. Dans certaines réactions de ce type, K1 diminue en fonction de température plus rapidement que k2 augmente, de sorte que k diminue en fonction de T, ce qui correspond à une énergie d'activation négative observée[8] - [9] - [10]
Un cas particulier d'une réaction de trois molécules est l'oxydation du monoxyde d'azote, . La loi de vitesse est avec[11] : = 35 (en valeur relative) à 0 °C, = 17,6 à 100 °C, = 11,3 à 300 °C. L'énergie d'activation est alors négative. Le mécanisme réactionnel proposé est en deux étapes[12] : et .
Certaines réactions de polymérisation deviennent réversibles à haute température en présence de la dépolymérisation. En conséquence la polymérisation cationique est souvent caractérisée par une énergie d'activation négative[13]. À la température plafond les vitesses de polymérisation et de dépolymérisation sont égales.
Les réactions enzymatiques dans la zone de température où l'enzyme se dégrade. La vitesse est alors de plus en plus lente quand la température augmente car l'enzyme est de moins en moins active ;
Références
- M. Laffitte, F. Rouquerol, La réaction chimique, tome 2 : aspects thermodynamiques (suite) et cinétiques, 1991, chap. 79, p. 211.
- Peter William Atkins, Éléments de chimie physique, De Boeck, , 2e éd., 250-252 p. (ISBN 2-7445-0010-0).
- Sarazin J., Verdaguer M. (1991), L'oxydoréduction, concepts et expériences, Éd. Ellipse, p. 169.
- Sarrazin J, Verdaguer M. (1991), L'oxydoréduction, concepts et expériences, Éd. Ellipses, p. 150.
- S. Zumdahl, Steven S., Chimie des solutions, 1er éd., Les Éditions CEC Inc., 1988, p. 72
- Matthew Bui, « The Arrhenius Law: Activation Energies », sur Chemistry LibreTexts, UC Davis (consulté le )
- Michael Mozurkewich et Sidney Benson, « Negative activation energies and curved Arrhenius plots. 1. Theory of reactions over potential wells », J. Phys. Chem., vol. 88, no 25, , p. 6429–6435 (DOI 10.1021/j150669a073).
- James H. Espenson, Chemical kinetics and reaction mechanisms, McGraw-Hill, (ISBN 0-07-019667-2), p. 121.
- Peter Atkins et Julio de Paula, Atkins' Physical Chemistry, W. H. Freeman, , 8e éd. (ISBN 0-7167-8759-8), p. 822.
- Tamara Kadir, « 3.2.2: Pre-equilibrium Approximation », sur Chem Libre Texts, (consulté le ) : « The overall activation energy is negative if Ea1 + Ea2 < Ea-1 »
- Schuffenecker K., Scacchi G., B. Proust, Foucaut J.-F., Martel L., Bouchy M. (1991), Thermodynamique et Cinétique chimiques, Éd. Tec et doc, coll. info chimie, p. 248.
- Peter William Atkins, Éléments de chimie physique, De Boeck, , 2e éd. (ISBN 2-7445-0010-0), p. 262
- J.M.G. Cowie, Polymers: Chemistry & Physics of Modern Materials, Blackie, , 2e éd. (ISBN 0-216-92980-6), p. 88.

























![{\displaystyle v=k\,\left[{\rm {NO}}\right]^{2}\,\left[{\rm {O_{2}}}\right]}](https://img.franco.wiki/i/ae77cc1d5a0ef31cc0ac2b83fbb421dcca3d9e68.svg)

