Semimétal

(en) Structure de bandes comparées de semiconducteurs à gap direct et à gap indirect, et de semimétaux typiques.

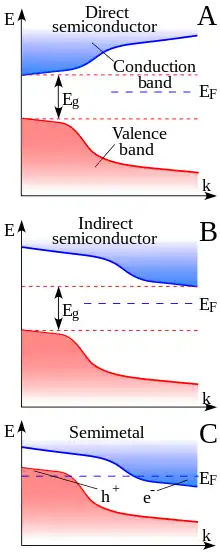
Outre la distribution de la densité d'états électroniques en fonction de l'énergie des porteurs, la structure de bandes d'un matériau fait également intervenir le vecteur d'onde k et le quasi-moment (quantité de mouvement) associé. Dans le cas des semiconducteurs, on distingue ainsi couramment les semiconducteurs à gap direct et à gap indirect selon que les états d'énergie les plus bas de la bande de conduction se trouvent à quantité de mouvement constant ou non par rapport aux états d'énergie les plus élevés de la bande de valence dans la première zone de Brillouin. La différence entre les états d'énergie les plus bas de la bande de conduction et les états d'énergie les plus élevés de la bande de valence définissent le gap du semiconducteur, indépendamment des quantités de mouvement associées.

Dans le cas des semimétaux, les états d'énergie les plus bas de la bande de conduction sont situés à un niveau légèrement inférieur aux états d'énergie les plus élevés de la bande de valence, de sorte qu'ils se recouvrent partiellement ; ils correspondent cependant à des quantités de mouvement distinctes, ce qui en fait en quelque sorte des matériaux à gap indirect négatif.

Dans la mesure où les semimétaux ont moins de porteurs que les métaux, leur conductivité électrique et leur conductivité thermique sont inférieures à celle des métaux. La masse effective des électrons et des trous y est également inférieure, dans la mesure où la superposition des bandes de valence et de conduction provient généralement de ce que ces bandes sont larges. Ils possèdent également généralement une suscpetibilité diamagnétique et une permittivité élevée.

Le profil de variation de la conductivité électrique en fonction de la température diffère sensiblement entre métaux et semimétaux. En effet, la conductivité d'un matériau dépend à la fois de la concentration des porteurs de charge électrique dans ce matériau, et de la mobilité de ces porteurs, deux grandeurs qui évoluent en sens inverse lorsque la température augmente. Ainsi, la concentration des porteurs tend plutôt à croître à mesure qu'ils sont injectés thermiquement dans la bande de conduction, tandis que leur mobilité décroît par diffusion sur les phonons du réseau cristallin, dont la concentration et l'énergie augmentent à mesure que le cristal se réchauffe.

Dans les métaux, les bandes de valence et de conduction se recouvrent largement, de sorte que la population de porteurs avec la température croît moins vite que la diffusion due aux phonons. Il s'ensuit que la conductivité décroît lorsque la température augmente. Dans les semiconducteurs, les bandes de valence et de conduction sont disjointes, de sorte que la conductivité est assurée à la fois par les électrons de la bande de conduction et par les trous de la bande de valence. Ces deux types de porteurs ont des mobilités différentes (quatre fois plus élevée pour les électrons que pour les trous dans le silicium, par exemple) tandis que leur concentration croît avec la température. Il s'ensuit que, si l'on fait croître la température d'un semiconducteur, sa conductivité commence par croître à basse température, puis décroît à température moyenne, avant de croître à nouveau à température élevée.

La structure de bandes des semimétaux les rapproche des métaux dans la mesure où ces matériaux n'ont pas de bande interdite, mais la faible densité d'états électroniques au niveau de Fermi scinde les porteurs en deux populations, électrons et trous, à l'instar des semiconducteurs. Lorsqu'on fait croître la température d'un semimétal, la concentration des porteurs est d'abord quasiment constante, comme dans les métaux, puis croît sensiblement, comme dans les semiconducteurs. On observe ainsi une transition semimétal-semiconducteur[6]. Celle-ci s'observe à température ambiante pour des semimétaux comme l'arsenic[7] et l'antimoine[8] - [9], mais à très basse température pour le bismuth massif — le bismuth peut se comporter comme un semiconducteur lorsqu'il est déposé en couches minces d'épaisseur inférieure à une valeur critique de 30 nm[10]. Il s'ensuit que, contrairement aux semiconducteurs, dont la conductivité est nulle au zéro absolu faute de porteurs, la conductivité des semimétaux est toujours non nulle, comme c'est le cas des métaux.