Résonance paramagnétique électronique

La résonance paramagnétique électronique (RPE), résonance de spin électronique (RSE), ou en anglais electron spin resonance (ESR) désigne la propriété de certains électrons à absorber, puis réémettre l'énergie d'un rayonnement électromagnétique lorsqu'ils sont placés dans un champ magnétique. Seuls les électrons non appariés (ou électrons célibataires), présents dans des espèces chimiques radicalaires ainsi que dans les sels et complexes des métaux de transition, présentent cette propriété.

Spectromètre à résonance paramagnétique électronique

Ce phénomène est utilisé dans la spectroscopie par résonance paramagnétique électronique. Celle-ci permet de mettre en évidence la présence d'électrons non appariés dans des solides, des liquides ou des gaz et de déterminer l'environnement de ces derniers. Il sera possible, par exemple, de connaitre le type de noyaux atomiques à proximité de ces électrons non appariés et d'en déduire éventuellement la structure d'une molécule.

La majorité des espèces chimiques stables possédant des paires d'électrons appariés, cette technique permettra de mettre en évidence les espèces chimiques possédant des électrons non appariés de manière très spécifique. Par ailleurs, du fait de l'importance du moment magnétique de spin de l'électron, cette technique est également très sensible.

La RPE est notamment utilisée en préhistoire et paléoanthropologie pour dater certains matériaux, tels que l'émail de dents fossiles, avec un champ d'application allant de 20 000 ans à 1 million d'années.

Terminologie

L'expression « spectroscopie par résonance paramagnétique électronique » laisse imaginer que seules des interactions paramagnétiques peuvent être étudiées. En réalité, des interactions de type ferromagnétiques, ferrimagnétiques ou antiferromagnétiques interviennent, surtout dans le cas des matériaux magnétiquement concentrés. Il serait donc préférable de désigner ce type de spectroscopie par l'expression plus générale de « spectroscopie par résonance de spin électronique » (RSE). Néanmoins, les applications utilisant cette spectroscopie concernent essentiellement des espèces paramagnétiques, d'où l'usage de « RPE » plus fréquent que celui de « RSE ».

Par ailleurs, dans le reste de cet article, l'expression « résonance de spin électronique » pourra désigner indifféremment la propriété électronique ou la spectroscopie associée.

Historique

La résonance de spin électronique a été découverte en 1944 par le physicien soviétique Ievgueni Zavoïski de l'université d'État de Kazan[1] ainsi que de manière concomitante et indépendante par Brebis Bleaney à l'université d'Oxford. La technique de la RSE en onde continue a longtemps été la plus utilisée. Dans celle-ci, le système est irradié en continu par un rayonnement micro-onde à une fréquence donnée. La RSE impulsionnelle est de plus en plus utilisée, notamment en biologie structurale où elle permet de connaître les distances entre radicaux, en science des matériaux pour connaître la structure locale autour de défauts paramagnétiques.

Une revue d'études portant sur le moyens de revigorer les semences (agricoles ou horticoles) avant plantation, publiée en 2016, estime que, dans le groupe des méthodes issues de l'électroculture (« magnéto-amorçage » en particulier) la résonance paramagnétique électronique aurait aussi un potentiel important en technologie des semences, mais entre à explorer afin d'évaluer comment et quand traiter au mieux la semence pour améliorer sa germination et croissance et par suite le rendement de la culture (meilleure dose, durée et moment d'irradiation...)[2].

Principe

Levée de dégénérescence entre moments magnétiques

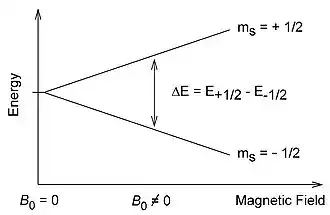
Séparation des niveaux d'énergie (pour le cas d'un spin S = 1/2) en présence d'un champ magnétique externe.

Le principe de la RSE repose sur l'effet Zeeman : soumis à l'action d'un champ magnétique extérieur H, les niveaux d'énergie d'un spin S se séparent en (2S + 1) états, chacun affecté d'un nombre quantique de spin $m_{S}$ ( $m_{S}$ = -S, -S+1, -S+2, ..., S). Cette séparation des niveaux est d'autant plus grande que H est intense (voir figure). Cette levée de dégénérescence d'états de spin électronique est identique à la levée de dégénérescence d'états de spin nucléaire qui permet la RMN.

Ainsi, pour le cas d'un ion paramagnétique ne présentant qu'un seul électron célibataire (donc pour lequel S = 1/2), la présence du champ magnétique extérieur donne lieu à (2S + 1) = 2 états, correspondant à $m_{S}=-1/2$ et $m_{S}=+1/2$ . L'énergie magnétique associée à chacun de ces états est $m_{S}g\mu _{B}H$ , où

$m_{S}$ est la valeur du nombre quantique de spin (+1/2 ou -1/2 pour l'électron libre)
$g$ est le facteur de Landé. Pour un électron libre, g_e = 2,0023
$\mu _{B}$ (parfois noté β) est le magnéton de Bohr ( $\mu _{B}$ = 9,2741 × 10⁻²⁴ J.T⁻¹).
$H$ est valeur du champ magnétique

Distribution de Maxwell-Boltzmann

Les électrons présents dans le système vont pouvoir occuper les différents niveaux électroniques. Au niveau macroscopique, la présence dans l'un ou l'autre niveau est déterminé par la statistique de Maxwell-Boltzmann :

${\frac {n(m_{S}=+1/2)}{n(m_{S}=-1/2)}}=\exp {\left(-{\frac {E(m_{S}=+1/2)-E(m_{S}=-1/2)}{k_{B}T}}\right)}=\exp {\left(-{\frac {\Delta E}{k_{B}T}}\right)}$

avec :

$k_{B}$ la constante de Boltzmann
$T$ la température de l'échantillon
$\Delta E$ la différence d'énergie entre les niveaux dégénérés.

Le niveau $m_{S}=-1/2$ est de ce fait légèrement plus peuplé que le niveau supérieur. Le rapport entre les populations de chacun des deux niveaux vaut 0,998, pour une énergie de 40 µeV (différence d'énergie observée pour un électron dans un champ de 3350 gauss) et une température de 298 K. De ce fait, la perturbation induite par le champ magnétique est relativement faible.

Absorption et émission d'onde électromagnétique

En présence d'une onde électromagnétique de fréquence ν (champ hyperfréquence ou micro-onde) perpendiculaire au premier et d'amplitude beaucoup plus faible, un photon peut être absorbé ou émis si son énergie hν est égale à la différence entre les niveaux $m_{S}$ -1/2 et 1/2 (soit $g\mu _{B}H$ ).

Ainsi, la condition de résonance se résume par :

$h\nu =E(m_{s}=1/2)-E(m_{s}=-1/2)=g\,\mu _{B}\,H\quad (Eq.1)$

avec les mêmes notations que précédemment ainsi que

$h$ la constante de Planck ( $h$ = 6,6261 × 10⁻³⁴ J.S) ;
$\nu$ la fréquence du champ micro-onde

D'une façon plus générale, lorsqu'il y a plus de 2 états, les transitions permises sont celles pour lesquelles les états (initial et final) satisfont aux conditions (appelées règle de sélection) ΔS = 0 et Δm_S = ± 1. Les autres transitions sont généralement interdites, sauf en cas de mélange entre les états quantiques.

La condition de résonance exprimée ci-dessus (Éq. 1) peut également s'écrire :

$\nu =g\,{\frac {\mu _{B}}{h}}H=\gamma \,H\quad (Eq.2)$

où γ désigne le rapport gyromagnétique.

Obtention des spectres de résonance

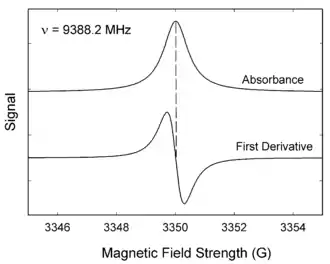
Spectres typiques d'absorption (courbe du haut) et de la dérivée première de l'absorption (courbe du bas) obtenus à fréquence fixe (bande X à 9388,2 MHz) et en faisant varier le champ magnétique statique externe.

La recherche de la résonance peut être effectuée en fixant le champ magnétique H et en faisant varier la fréquence de l'onde électromagnétique ν, comme cela est couramment réalisé en RMN. Une autre possibilité, plus fréquemment employée, est de fixer la fréquence de l'onde électromagnétique (elle sera, par exemple, à 9388,2 MHz pour un spectromètre utilisant la bande X) et de faire varier le champ magnétique.

De ce fait, les diagrammes présentent de manière classique l'absorbance ou sa dérivée en ordonnée et le champ magnétique statique H en abscisse, exprimé en gauss, comme cela est illustré par la figure ci-contre.

La plupart des spectromètres de RSE utilisent une détection synchrone, c'est-à-dire que le champ magnétique est modulé autour d'une valeur centrale telle que

$H=H_{0}+H_{1}\,\cos(\omega \,t)$

Le signal d'absorption peut s'écrire à l'ordre 1 sous la forme : $A=A(H_{0})+\left({\frac {dA}{dH}}\right)_{0}\,\cos(\omega \,t)$

En filtrant la fréquence correspondant à ω, la courbe dérivée ${\frac {da}{dH}}$ est obtenue.

Chaque signal ainsi enregistré est caractéristique de l'élément magnétique en présence et des interactions que cet élément ressent. Ces informations s'obtiennent à partir de :

la valeur du champ de résonance (qui informe sur le facteur g de l'ion magnétique en question) ;
l'aire en dessous de la courbe d'absorption (qui informe, entre autres, sur le nombre de spins présents) ;
la mi-largeur à mi-hauteur de la courbe d'absorption (qui informe sur les interactions auxquelles les spins sont soumis).

Couplage hyperfin

Le nombre de signaux indique parfois le nombre de sites ou bien des interactions hyperfines avec un (ou plusieurs) spins nucléaires (pour des détails, voir Hyperfine structure (en)).

En effet, l'hamiltonien d'un électron de spin ${\vec {S}}$ couplé à un champ magnétique ${\vec {B}}_{0}$ , entouré de $n$ noyaux à spin non nuls ${\vec {\widehat {I}}}_{k}$ , est donné par la somme de trois termes[3] :

${\widehat {H}}={\widehat {h}}_{Zeeman}+{\widehat {h}}_{Spin-orbite}+{\widehat {h}}_{Structure\,hyperfine}$

Les termes ${\widehat {h}}_{Zeeman}$ et ${\widehat {h}}_{Spin-orbite}$ peuvent être regroupés et approximés dans le cadre de la théorie de la perturbation par le terme : ${\frac {\mu _{B}}{h}}{\vec {S}}{\widehat {g}}{\vec {B}}$ , avec ${\widehat {g}}$ une matrice hermitienne carrée de dimension 3.

Le terme de structure hyperfine, lui-même constitué de deux composantes : le terme d'interaction magnétique dipôle-dipôle et le terme d'interaction par contact de Fermi ((en) Fermi contact interaction) lié au fait que l'électron a une probabilité non nulle de se trouver au niveau du noyau.

Afin de simplifier certains spectres, il peut être opportun d'ajouter un rayonnement radiofréquence du type de ceux utilisés en RMN. Il s'agit alors de résonance double électronique et nucléaire, ou (en) ENDOR.

Équipement

De la même manière que la spectroscopie RMN, cette technique utilise des champs magnétiques de l'ordre de grandeur du tesla. Pour cela, des bobines constituées de matériaux supra-conducteurs sont employées, dans lesquelles est introduite une intensité électrique importante. La circulation de ce courant électrique dans une bobine est à l'origine de ce champ magnétique. Afin de permettre la supraconductivité de ces matériaux, les bobines sont refroidies par de l'hélium liquide.

Le champ radiofréquence est, lui, généré par des bobines conventionnelles.

Applications

Analyse des matériaux

La RSE est utile pour l'étude de la structure locale de l'ensemble des matériaux pouvant présenter en leur sein un élément paramagnétique, utile pour pouvoir décrire l'environnement local. Elle peut servir à l'étude, par exemple, de défauts créés par le passage d'un rayonnement (α, β, γ, particules chargées...), donnant ainsi une mesure absolue de leur concentration dans la structure (à condition d'avoir un étalon). On peut étudier des ions paramagnétiques dans les structures de complexes dans les composés organiques ou de minéraux. De nombreux objets peuvent ainsi être étudiés grâce à cette technique, allant des matériaux désordonnés (verres) à des structures cristallines (minéraux) en passant par des matériaux organiques.

L'exploitation des spectres RSE passe parfois par une étape de simulation afin de pouvoir en déduire les différentes informations concernant l'environnement des éléments paramagnétiques présents et de suivre l'évolution du système en fonction des conditions expérimentales et de mesure.

Datation archéologique

La RSE est également utilisée dans le cadre de datations en archéologie préhistorique. Alors que la thermoluminescence s'applique aux cristaux de quartz et de feldspath, la RSE s'applique aux cristaux de quartz, calcite, apatite (os et dents), sulfates et phosphates qui ont subi des bombardements radio-actifs naturels, venant des sols (sédiments et roches ambiants), endommageant les mailles cristallines de minéraux cristallisés en déplaçant des électrons qui sont ensuite piégés dans d'autres défauts de la maille. Ces cristaux, chauffés (par action naturelle ou humaine), exposés à la lumière (cas des sédiments avant enfouissement) ou nés d'une nouvelle cristallisation, ont leurs pièges vidés, ce qui remet l'horloge à zéro. La datation consiste à mesurer l'accumulation, qui est fonction du temps, des électrons à nouveau piégés[4]. La RSE s'applique en particulier à l'émail dentaire de grands mammifères fossiles, à des grains de quartz extraits de sédiments archéologiques ou à des carbonates (stalagmites, coraux, etc.). Son champ d'application est très étendu, d'environ 20 000 ans à un million d'années[5].

Études de mécanismes réactionnels

La RPE permet de sonder les intermédiaires réactionnels lors de réactions chimiques par voie radicalaire. Cela permet de progresser dans la connaissance des mécanismes réactionnels.

Autres

La RSE s'applique aussi aux modèles biologiques.

La RPE s'est avérée une technique de choix pour déterminer les paramètres associés à la fluidité membranaire.

La RPE a été utilisée pour mesurer la quantité d'énergie appliquée à l'échelle moléculaire lors de réactions mécanochimiques[6].

Notes et références

Spectrométrie de résonance de spin électronique
Susana de Sousa Araújo, Stefania Paparella, Daniele Dondi et Antonio Bentivoglio, « Physical Methods for Seed Invigoration: Advantages and Challenges in Seed Technology », Frontiers in Plant Science, vol. 7,‎ 12 mai 2016 (ISSN 1664-462X, PMID 27242847, PMCID PMC4863893, DOI 10.3389/fpls.2016.00646, lire en ligne, consulté le 20 octobre 2020)
A. Schweiger and G. Jeschke, Principles of pulse electron paramagnetic resonance. Oxford University Press, 2001, États-Unis
Pierre-Roland Giot, Jean L'Helgouach, Jean Laurent Monnier, Préhistoire de la Bretagne, Éd. Ouest-France, 1998 (lire en ligne), p. 26.
Étienne Roth (dir.), Bernard Poty (dir.), Gérard Poupeau, Alexandre Rossi et al. (préf. Jean Coulomb), Méthodes de datation par les phénomènes nucléaires naturels, Paris, Éditions Masson, coll. « Collection CEA », 1985, 631 p. (ISBN 2-225-80674-8), chap. 10 (« Datations par résonance de spin électronique »)
M. Baron, A. Chamayou, L. Marchioro, J. Raffi. (2005). "Radicalar probes to measure the action of energy on granular materials". Adv. Powder Technol 16 (3): 199–212. doi:10.1163/1568552053750242.

Annexes

Bibliographie

(en) A. Abragam et B. Bleaney, Electron paramagnetic resonance of transition ions, New York, Dover Publications, 1986, 911 p. (ISBN 978-0-486-65106-4, OCLC 13360841)
(en) A. Schweiger et G. Jeschke, Principles of pulse electron paramagnetic resonance, Oxford University Press, 2001, États-Unis
(en) M. Baron, A. Chamayou, L. Marchioro, J. Raffi (2005), Radicalar probes to measure the action of energy on granular materials, Adv. Powder Technol. 16 (3), p.199–212, doi:10.1163/1568552053750242

Lien externe

[PDF] Spectrométrie de résonance paramagnétique électronique - RPE

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.