Plus grand commun diviseur de nombres entiers

Tout nombre entier n a pour diviseur 1, puisque n = n×1. Pour deux nombres entiers a et b, l'ensemble D de tous leurs diviseurs communs, n'est donc pas vide, puisqu'il contient 1.

L'ensemble des diviseurs d'un nombre entier non nul est fini a : tous les diviseurs sont inférieurs à a. Le PGCD de deux nombres entiers a et b dont au moins l'un des deux est non nul peut donc être défini comme le plus grand nombre appartenant à l'ensemble D de tous les diviseurs communs de a et b.

En particulier, comme tout nombre entier est un diviseur de zéro (car 0 × c = 0 quel que soit c) :

• pour tout entier a > 0, PGCD(a, 0) = PGCD(0, a) = a.

Cette définition ne s'étend pas à PGCD(0, 0), puisqu'il n'existe pas de plus grand diviseur de 0.

Mais il est aussi possible de prendre « plus grand » au sens de la divisibilité : (b est plus grand que a quand b est un multiple de a, soit a est un diviseur de b), ce qui conduit à la définition suivante :

• PGCD(a,b) est un diviseur de a et un diviseur de b ;
• si c est un diviseur de a et b alors c est un diviseur de PGCD(a,b) ;
• PGCD(a,b) ≥ 0.

Un tel entier existe bien, et il en existe un seul vérifiant ces trois propriétés qui est le PGCD au sens de la définition précédente quand (a,b) ≠ (0,0). Avec cette définition PGCD(0,0)=0.

La troisième condition PGCD(a,b) ≥ 0 n'est bien sûr pas utile quand on travaille sur les entiers naturels, où la relation de divisibilité est une relation d'ordre. Elle est nécessaire pour l'unicité dans le cas des entiers relatifs : en général deux nombres vérifient les deux premières conditions, le PGCD usuel et son opposé. Par exemple, deux nombres D vérifient

• D divise 30 et 18 ;
• tout entier qui divise 30 et 18 divise aussi D ;

à savoir 6 et -6.

Cette définition est aussi la plus susceptible d'être étendue à d'autres anneaux, comme l'anneau des polynômes à coefficients réels.

En appliquant directement la définition on a :

• PGCD(a,a) = a ;
• plus généralement, si a est un diviseur de b, alors PGCD(a,b) = a ;
• si p est premier, alors PGCD(p, a) = 1 ou PGCD(p, a) = p.

Le PGCD de deux nombres entiers positifs a et b est lié avec leur PPCM (le plus petit de leurs multiples communs), par la relation

ab = PGCD(a, b)×PPCM(a, b).

Pour trois entiers relatifs non nuls a, b, c :

• pgcd(a, b) × ppcm(a, b) = |ab|
• ${\displaystyle \operatorname {pgcd} (a,\operatorname {ppcm} (b,c))=\operatorname {ppcm} (\operatorname {pgcd} (a,b),\operatorname {pgcd} (a,c))}$
• ${\displaystyle \operatorname {ppcm} (a,\operatorname {pgcd} (b,c))=\operatorname {pgcd} (\operatorname {ppcm} (a,b),\operatorname {ppcm} (a,c))}$

• Soient a, b deux entiers non nuls, il est possible de remplacer l'un de deux nombres a ou b par a + b, ou par a - b, sans changer le PGCD.

${\displaystyle \operatorname {pgcd} (a,b)=\operatorname {pgcd} (a,b+a)=\operatorname {pgcd} (a,b-a)}$ ;

• par conséquent, on peut ajouter ou retrancher à l'un des deux un multiple de l'autre. Plus formellement :

Cette propriété fonde l'algorithme d'Euclide, une méthode qui permet de déterminer le PGCD de deux nombres (voir plus bas).

• Le PGCD est compatible avec la multiplication par un entier naturel : soit k un entier naturel,

${\displaystyle \operatorname {pgcd} (ka,kb)=k\operatorname {pgcd} (a,b)}$[2].

Par exemple PGCD(9, 12) = 3, en multipliant par 3 on obtient PGCD(27, 36) = 9.

• Une combinaison linéaire quelconque de a et b, c'est-à-dire un nombre de la forme au + bv, où u et v sont des entiers relatifs, est forcément un multiple de tout diviseur commun de a et b, en particulier de PGCD(a, b).
  On peut montrer (théorème de Bachet-Bézout) que le PGCD(a, b) est lui-même une combinaison linéaire de a et b. C'est donc la plus petite combinaison strictement positive :

  ${\displaystyle \operatorname {pgcd} (a,b)=\min \left(\left\{au+bv\mid (u,v)\in \mathbb {Z} ^{2}\right\}\cap \mathbb {N} ^{*}\right)}$.

Clairement, tout diviseur du PGCD de deux nombres est aussi un diviseur commun de ces deux nombres. La réciproque est vraie y compris pour la première définition. Par exemple, si le PGCD de deux nombres entiers a et b est 6, les diviseurs communs à a et b seront ceux de 6, soit : 1, 2, 3, 6 et leurs opposés.

C'est une conséquence du théorème de Bachet-Bezout, un diviseur commun de a et b étant un diviseur d'une combinaison linéaire de ceux-ci. La propriété se démontre aussi directement par récurrence, en suivant l'algorithme d'Euclide

Les diviseurs communs de deux nombres entiers sont donc exactement les diviseurs de leur PGCD. Cette propriété permet de démontrer l'équivalence des deux définitions ci-dessus.

Par exemple, si le PGCD de deux nombres entiers a et b est 6, les diviseurs communs à a et b seront ceux de 6, soit : 1, 2, 3, 6 et leurs opposés.

${\displaystyle \operatorname {pgcd} (a,b,c)=\operatorname {pgcd} (\operatorname {pgcd} (a,b),c)=\operatorname {pgcd} (a,\operatorname {pgcd} (b,c))}$. On peut étendre à un nombre arbitraire d'éléments.

Des nombres entiers naturels sont dits premiers entre eux lorsqu'ils n'ont pas d'autre diviseur commun que 1, autrement dit, leur PGCD est égal à 1.

Si deux nombres entiers a et b ont pour PGCD le nombre d, alors les entiers a/d et b/d sont premiers entre eux[4].

D'après le théorème fondamental de l'arithmétique, tout entier n naturel non nul s'écrit de manière unique à l'ordre près des facteurs comme un produit fini de nombres premiers. Le nombre de fois que l'entier premier p apparait dans cette écriture s'appelle la valuation p-adique de n, notée v_p(n). Un entier non nul m divise n si et seulement si pour tout p, v_p(m) ≤ v_p(n).

De fait, le pgcd d'une famille (a_i) d'entiers naturels est donné par :

${\displaystyle \mathrm {pgcd} (a_{i})=\prod _{p}p^{\min v_{p}(a_{i})}}$

où le produit porte sur l'ensemble des nombres premiers (presque tous les facteurs du produit, hormis une quantité finie, sont égaux à 1).

On en déduit à nouveau que tout diviseur commun à une famille d'entiers non tous nuls divise leur pgcd.

Toute suite de Lucas x_n = U_n(P, Q) associée à des paramètres P, Q premiers entre eux est à divisibilité forte, c.-à-d. : ${\displaystyle \operatorname {pgcd} (x_{m},x_{n})=x_{\operatorname {pgcd} (m,n)}}$ C'est le cas, par exemple, de :

• la suite de Fibonacci U_n(1, –1) (cf. « propriété 6 » de la suite de Fibonacci) ;
• la suite U_n(b + 1, b) = (bⁿ – 1)/(b – 1) des répunits en base b (pour tout entier b > 1) donc ${\displaystyle \operatorname {pgcd} (b^{m}-1,b^{n}-1)=b^{\operatorname {pgcd} (m,n)}-1}$.

Une fraction irréductible est une fraction dans laquelle le numérateur et le dénominateur sont les plus proches possibles de 1. Cela revient à dire que le numérateur et le dénominateur sont premiers entre eux. La fraction irréductible égale à une fraction a/b donnée est celle dont le numérateur est a/d et le dénominateur b/d, où d = PGCD(a, b).

Certaines équations diophantiennes (c'est-à-dire des équations dont les paramètres et les solutions cherchées sont des nombres entiers) se résolvent par une division par un PGCD afin de se ramener à une équation équivalente mettant en jeu des nombres premiers entre eux.

Ainsi l'équation diophantienne ax + by = c d'inconnues x et y admet une infinité de solutions si et seulement si c est un multiple du PGCD de a et b. Lorsque c n'est pas un multiple du PGCD de a et b, elle n'admet aucune solution entière. Ces résultats sont une conséquence du théorème de Bachet-Bézout. La méthode classique de résolution d'une telle équation consiste à diviser l'équation par le PGCD de a et b, puis, en s'appuyant sur le théorème de Gauss, résoudre la nouvelle équation obtenue, de la forme a'x + b'y = c', où a' et b' sont premiers entre eux.

Une autre équation diophantienne classique est la recherche des triplets pythagoriciens. Un triplet pythagoricien est la donnée de trois nombres entiers x, y et z qui vérifient la relation de Pythagore : x² + y² = z². Cela revient à chercher tous les triangles rectangles dont les longueurs des côtés sont des nombres entiers. L'étude de cette équation se ramène à la recherche des nombres x, y et z premiers entre eux : si x, y et z sont des solutions de l'équation et que d est leur PGCD, alors x/d, y/d et z/d sont aussi des solutions de l'équation.

La décomposition en facteurs premiers permet de calculer le PGCD (voir #PGCD et facteurs premiers) : pour tout nombre premier p,

${\displaystyle v_{p}({\text{pgcd}}(a,b))=\min(v_{p}(a),v_{p}(b))}$,

où ${\displaystyle v_{p}}$ est la valuation p-adique.

La première étape de cette méthode consiste à décomposer a et b en produits de nombres premiers. Si ${\displaystyle a=p_{1}^{\alpha _{1}}\times p_{2}^{\alpha _{2}}\times \cdots \times p_{k}^{\alpha _{k}}}$ et ${\displaystyle b=p_{1}^{\beta _{1}}\times p_{2}^{\beta _{2}}\times \cdots \times p_{k}^{\beta _{k}}}$ où tous les exposants vérifient ${\displaystyle \alpha _{i}\geq 0}$ et ${\displaystyle \beta _{i}\geq 0}$ alors le PGCD est donné par :

${\displaystyle \mathrm {pgcd} \left(a,b\right)=p_{1}^{\min \left(\alpha _{1},\beta _{1}\right)}\times p_{2}^{\min \left(\alpha _{2},\beta _{2}\right)}\times \cdots \times p_{k}^{\min \left(\alpha _{k},\beta _{k}\right)}}$. Cependant le calcul de la décomposition en facteurs premiers est coûteux, cette méthode n'est pas utilisée en pratique (hors illustration à visée pédagogique).

Connaissant les décompositions en facteurs premiers de deux nombres entiers a et b, la décomposition en facteurs premiers de leur PGCD est constituée des mêmes facteurs que ceux de a et b, en prenant pour chaque facteur l'exposant minimal qui apparaît à la fois dans a et b : le plus petit exposant commun à a et b.

Une variante, pas fondamentalement plus efficace, est de calculer directement la décomposition en facteurs premiers du PGCD : en prenant les nombres entiers dans l'ordre, on teste pour chacun s'ils sont diviseurs communs à a et b. C'est-à-dire que l'on trouve un nombre k tel que a = ka′ et b = kb′, alors il suffit de calculer le PGCD de a′ et b′ car on a : ${\displaystyle \mathrm {pgcd} \left(a,b\right)=\mathrm {pgcd} \left(ka^{\prime },kb^{\prime }\right)=k~\mathrm {pgcd} \left(a^{\prime },b^{\prime }\right).}$

Exemple : pgcd(60,84). On voit successivement que : ${\displaystyle \mathrm {pgcd} \left(60,84\right)=2\times \mathrm {pgcd} \left(30,42\right)=2\times 2\times \mathrm {pgcd} \left(15,21\right)=2\times 2\times 3\times \mathrm {pgcd} \left(5,7\right)}$. Or, ${\displaystyle \mathrm {pgcd} \left(5,7\right)=1.}$, car 5 est premier, et ne divise pas 7. Donc, ${\displaystyle \mathrm {pgcd} \left(60,84\right)=2\times 2\times 3=12}$.

Animation de l'algorithme d'Euclide par soustractions successives.

Le PGCD de deux nombres a et b est aussi celui de a et de b - a. Ceci justifie la méthode des soustractions successives employée par Euclide pour le calcul du PGCD, connue en histoire des mathématiques sous le nom d'anthyphérèse. Elle repose sur les équations suivantes :

Algorithme d'Euclide par soustraction

pgcd(a,b) = pgcd(a, b - a) pour b ≥ a > 0

pgcd(a,b) = pgcd(b, a) pour a > b > 0 ou a = 0

pgcd(a, 0) = a

Exemple : pgcd(75, 60) = pgcd(60,75) = pgcd(60, 15) = pgcd(15,60)= pgcd(15,45) = pgcd(15, 30) = pgd(15, 15) = pgcd(15, 0) = 15.

Algorithme d'Euclide.

Dans l'algorithme d'Euclide par soustraction, pour le calcul de pgcd(a, b), a ≤ b, a est soustrait successivement de b jusqu'à obtenir r < b. C'est le reste de la division euclidienne de a par b. Ce reste peut se calculer plus efficacement que par soustractions successives, en particulier si a est très supérieur à b.

L'algorithme d'Euclide est souvent donné en utilisant directement la division euclidienne, plus précisément le reste. Le reste de la division de a par b, avec b > 0, noté ici reste(a, b), qui est l'unique entier naturel vérifiant :

1. a = bq + reste(a, b) pour un certain q (le quotient) ;
2. 0 ≤ reste(a, b) < b.

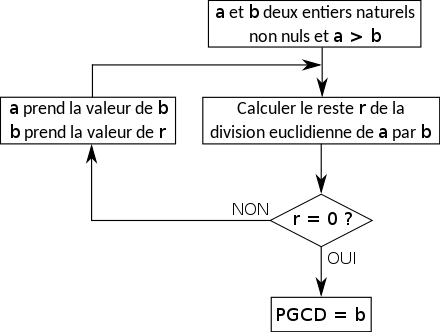
L'algorithme d'Euclide par division euclidienne s'appuie sur la même propriété que celui par soustraction, dont on déduit que a et b ont même PGCD que b et reste(a, b), plus précisément il s'appuie sur les équations suivantes :

Algorithme d'Euclide

pgcd(a, b) = pgcd( b, reste(a, b) ) pour b ≠ 0

pgcd(a, 0) = a

Comme, par définition de la division euclidienne, reste(a, b) < b, le second terme décroît strictement tant qu'il est strictement positif, d'où la terminaison de l'algorithme avec une valeur nulle pour ce second terme.

En reprenant le même exemple que pour l'algorithme par soustraction on obtient :

Exemple : pgcd(75, 60) = pgcd(60, 15) = pgcd(15, 0) = 15.

L'algorithme du PGCD binaire est une variante de l'algorithme d'Euclide qui est utile quand les nombres sont codés en binaire.

• André Deledicq, Mathématiques Lycée : tout le programme de la seconde à la terminale, Éditions de la Cité, 1998
• Michel Demazure, Cours d'algèbre, Cassini, 2008 (ISBN 978-2-84225-127-7)
• W. Gellert, H. Küstner, M. Hellwich et H. Kästner (trad. de l'allemand par un collectif, sous la direction de Jacques-Louis Lions), Petite encyclopédie des mathématiques [« Kleine Enzyklopädie der Mathematik »], Didier, 1980