Accueil🇫🇷Chercher

Observation mathématique de la pyramide de Khéops

La pyramide de Khéops a été scrutée et mesurée avec autant de précision que possible par des chercheurs issus de différents domaines depuis le début du XIXe siècle. De ces mesures ont découlé plusieurs hypothèses sur la volonté de ses concepteurs d'utiliser quelques éléments mathématiques dans ses proportions.

Conventions

Afin de comparer les différents résultats et d'analyser les intentions des concepteurs, les mesures sont exprimées en coudées égyptiennes. La pyramide avait ainsi, à l'origine, une base de 440 coudées et une hauteur de 280 coudées. La pente de ses faces est alors donnée par le rapport 280/220 soit 14/11. Ce rapport, étant un nombre sans dimension, reste bien entendu le même quelle que soit l'unité de mesure considérée.

L’origine de la pente 14/11 de la grande pyramide
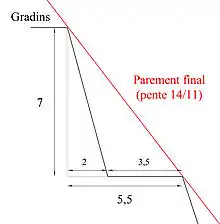
Apparition de la pente 14/11 à Meïdoum

Cette pente de l'apothème de la pyramide n'est pas la seule qui fut mise en œuvre par les anciens Égyptiens pour la construction des pyramides. La pyramide de Meïdoum connut plusieurs changements de plans. Initialement conçue comme une pyramide à degrés, elle fut par la suite recouverte d'un parement lui ayant donné l'apparence d'une pyramide à faces lisses. La pente des faces de ses gradins était de 7/2 et le rapport entre la hauteur d'un gradin et sa largeur de 2/1 (ou 7/3,5). Le parement étant parallèle à la ligne joignant les sommets des gradins, sa pente est donc de 7/5,5 soit 14/11, valeur de la pente finale des faces de la pyramide[1]. Cette valeur fut donc pour la première fois appliquée à la pyramide de Meïdoum mais ne constitue pas une règle chez les constructeurs de l'Ancien Empire puisque certaines pyramides ont une pente de 17/18 (pyramide rouge), 4/3 (pyramide de Khéphren) ou encore 7/5 (pyramide rhomboïdale).

Le nombre pi et le nombre d’or
Proportions de la grande pyramide

Quand on étudie la géométrie de la grande pyramide, il est délicat de faire la distinction entre les intentions des constructeurs et les propriétés qui découlent des proportions de l'édifice. On mentionne souvent le nombre d'or φ et le nombre Pi présents dans les proportions de la pyramide : les Égyptiens ont, nous l'avons vu, choisi une pente pour les faces de 14/11.

  • Concernant le nombre d'or, la proportion de 14/11 entraîne un rapport apothème/demi-base égal à , proche de [2].
  • La valeur du nombre serait donnée par le rapport (demi-périmètre de la base)/hauteur. On obtient ainsi la valeur approchée [2].

Ces deux résultats découlent donc de l'utilisation d'une pente de 14/11. S'il faut y voir une volonté délibérée de les inscrire dans la construction, le mérite en reviendrait à l'architecte qui utilisa pour la première fois cette pente à la pyramide de Meïdoum, achevée sous le règne de Snéfrou. Mais cette proposition est peu plausible[3]. D'après les quelques rares documents mathématiques recueillis à ce jour, les Égyptiens de l'Antiquité n'avaient aucune connaissance du nombre π et n'utilisaient que le nombre de substitution 256/81 = 3,1605 pour calculer l'aire d'un disque, méthode de calcul déjà mentionnée notamment dans le Papyrus Rhind datant du Moyen Empire (voir aussi Géométrie dans l'Égypte antique).

Relations de surfaces
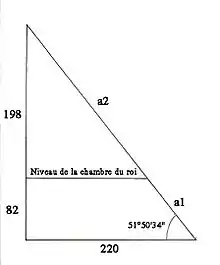
Relations pour le calcul des surfaces de la base et du niveau de la chambre du roi.
Relations entre les surfaces de la base et du niveau de la chambre du roi (mesures en coudées).

Il existe une relation remarquable entre l'aire de la base de la pyramide et l'aire du niveau de la chambre du roi, dont le sol se situe à 82 coudées[4] au-dessus du niveau du sol. L'aire de la base vaut 4402 coudées2, soit 193 600 coudées2 soit encore 2×96 800 coudées2. Les côtés du niveau de la chambre du roi valent 2×(220 – 82×11/14) = 311,14 coudées. L'aire de ce niveau est donc égale à 96 809,88 coudées2.

Première propriété : l'aire du niveau de la chambre du roi est égale, à 0,01 % près, à la moitié de l'aire de la base de la pyramide.

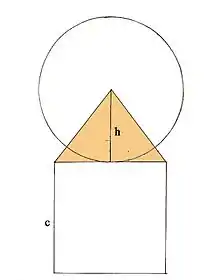
Cercle de rayon h et base de côté c (périmètres égaux).

De nombreuses relations sont également le fait de ce rapport 14/11. Tout d'abord, la circonférence du cercle[5], dont le rayon est la hauteur de la pyramide (soit 280 coudées), est égale au périmètre de la base de la pyramide (dont les côtés mesurent 440 coudées).

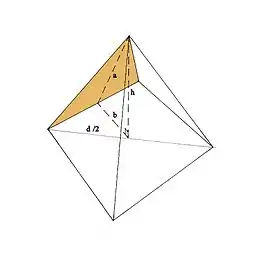
Relations entre la hauteur et l'aire des faces.

En effet, la circonférence du cercle est donnée par 2×π×280 = 1 759,3 coudées et le périmètre du carré par 440×4 = 1 760 coudées.

Deuxième propriété : Le périmètre de la base de la pyramide est égal, à 0,02 % près, à la circonférence du cercle dont le rayon est la hauteur de la pyramide.

Observez que l'on obtient 0,00023 % d'erreur si l'on utilise π = 3,14285 (voir § Le nombre π et le nombre d’or).

L'aire des quatre faces de la pyramide, si l'on néglige le phénomène de creusement des faces au niveau de l'apothème (voir Le phénomène d'apothème), est donnée par a×c/2 soit 356,09×440/2 = 78 339,8 coudées2 et h2 = 2802 = 78 400 coudées2. Par conséquent ces deux valeurs sont égales à 2×(78400 – 78339,8)/(78400 + 78339,8) = 0,08 % près.

Troisième propriété : L'aire de chacune des faces de la pyramide est égale, à 0,001 % près, à la hauteur de la pyramide élevée au carré.

Observations mathématiques et astronomie

L’orientation de la pyramide suivant les quatre points cardinaux

Il s'agit de la propriété la plus remarquable d'un point de vue technique, et tous s'accordent sur le fait qu'elle fut bien l'intention des constructeurs. C'est l'égyptologue Petrie qui, au XIXe siècle, est le premier à avoir attiré l'attention sur l'extraordinaire précision obtenue par les anciens Égyptiens[6]. Les quatre faces mesurent à leur base : 230,454 m au sud, 230,253 m au nord, 230,357 m à l'ouest et 230,394 m à l'est. L'erreur obtenue pour un carré parfait est de seulement 20 cm (seulement 4,4 cm selon Mark Lehner[7]). La pyramide est orientée suivant les quatre points cardinaux avec une erreur moyenne de 3'. L'erreur moyenne sur les angles droits de la base est également de 3'. La base de la pyramide a été nivelée avec une erreur de quelques centimètres.

La pyramide et l’étoile polaire
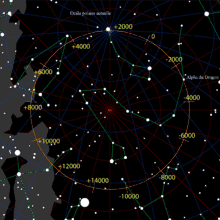
La précession des équinoxes (position de l'étoile polaire vers -2650).

La précession des équinoxes est un changement de direction de l'axe de rotation de la terre. Cet axe de rotation pointe actuellement vers l'étoile polaire, l'étoile la plus brillante de la constellation de la Petite Ourse. Cette précession a pour effet de provoquer un mouvement apparent des étoiles de la voûte céleste, et par conséquent de l'étoile polaire. Si l'on remonte à l'époque de la construction de la grande pyramide (v. -2650), Alpha du Dragon (aussi appelée Thuban) de la constellation du Dragon[8] était au plus proche de l'axe de rotation de la terre allant même jusqu'à ne s'en éloigner que de 0,5° vers -2800. De nombreux auteurs[9] affirment que, le conduit nord de la chambre du roi ou la descenderie, pointaient vers l'étoile polaire de l'époque, Alpha du Dragon. Il y a un moyen très simple de déterminer l'angle d'inclinaison d'une galerie destinée à viser l'étoile polaire. Il faut que cet angle soit égal à la latitude du lieu où se trouve cette galerie, soit ici la latitude de la pyramide de Khéops qui est de 29° 58' 44". Or, d'une part l'angle de la descenderie est de 26° 26' 46"[10], et d'autre part l'angle du conduit de ventilation nord de la chambre funéraire est de 32° 30'[11].

En conclusion, ni les conduits ni la descenderie ne pointent (ni ne pointaient) le pôle céleste, aucun d'entre eux ne pointant l'étoile Alpha du Dragon à la date mentionnée ci dessus.

La pyramide et l’étoile Alnitak de la constellation d’Orion
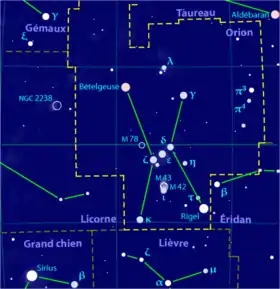
Alnitak (Zeta, à gauche de la ceinture d'Orion)
Sirius en bas à gauche.

Il y eut de nombreuses théories visant à faire de la pyramide un observatoire astronomique. Les couloirs de ventilation côté sud auraient pointé pour l'un (celui de la chambre de la reine) vers l'étoile Sirius, et pour l'autre (celui de la chambre du roi) vers l'étoile Alnitak. Or le couloir de ventilation sud de la chambre du roi est incliné suivant un angle de 45° par rapport à l'horizontal[11]. Il pointe donc un point du ciel dont l'altitude est égal à 45° alors que l'altitude de l'étoile Alnitak, à cette époque était de 44° 23' à son zénith[12]. Un écart de moins de 1° qui ne permettait pas cependant d'avoir une visée directe de l'étoile.

La pyramide et l’étoile Sirius de la constellation du Grand Chien

Une autre théorie affirme que le conduit de ventilation sud de la chambre de la reine pointait l'étoile Sirius qui, à l'époque avait une altitude à sa culmination de 37° 10'[12]. Or ce conduit, incliné de 38° 28'[13], pointe un endroit du ciel dont l'altitude est égale à cette valeur angulaire, une position différente de Sirius de plus d'un degré.

Toutes les étoiles du ciel (hormis l'étoile polaire) ont un mouvement apparent dû à la rotation de la terre sur elle-même, rotation complète effectuée en 24 heures. Ce mouvement implique que, si une étoile (Sirius ou Alnitak) était effectivement visée, alors le but n'était atteint que durant quelques dizaines de secondes, les étoiles étant animées de ce mouvement apparent qui semble les faire parcourir le ciel nocturne. De plus, les deux étoiles n'atteignent pas leur zénith en même temps, Sirius étant d'abord dans l’axe du couloir sud de la chambre de la reine, puis c’est au tour d’Alnitak d’être dans l’axe du conduit sud de la chambre du roi.

Enfin, il faut noter dans le cas où ce fut l'intention des constructeurs de viser ces étoiles, le fait étrange que les conduits de la chambre de la reine n'étaient pas rectilignes mais accusent au contraire un changement d'axe et de surcroit ils étaient bouchés au niveau de la chambre et s'arrêtent à quelques mètres de la surface du monument rendant toute observation de ce fait impossible. De plus dans l'hypothèse d'un changement de plan dans la construction, les rôles différents attribués aux conduits de la chambre du roi et de la chambre de la reine cadrent mal avec un projet calculé sur les astres.

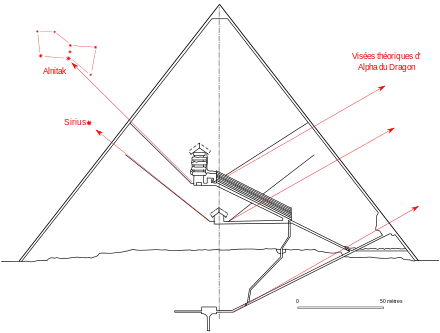
Étoiles « visées » par les conduits de la grande pyramide.

La géométrie de la distribution interne

Les conduits de ventilation

Une propriété géométrique semble avoir été voulue par l'architecte de la grande pyramide. Les conduits de ventilation de la chambre de la reine atteindraient tous les deux le même niveau de la pyramide. Ce fait est vérifié pour les conduits de la chambre du roi[11]. Cette théorie s'oppose à celle, astronomique, exposée ci-dessus.

Le conduit sud de la chambre de la reine est incliné d'un angle de 38° 28' et le conduit nord, d'un angle de 37° 28'[13]. Ces deux conduits suivent donc le chemin le plus court parvenant à la surface de la pyramide[14]. Ces angles correspondent, approximativement, à une pente de 11/14, l'inverse de la pente de 14/11 de l'apothème de la pyramide.

Le conduit sud de la chambre du roi est incliné d'un angle de 45° correspondant à une pente simple de 1/1 et le conduit nord, d'un angle de 32° 30' correspondant à une pente de 7/11[11].

Géométrie des conduits de ventilation (selon Gilles Dormion).

John Legon[15] a développé une théorie visant aussi à relever des propriétés géométriques induites par les dispositions des conduits. Mais ce dernier pousse le raisonnement plus loin en corrélant adroitement plusieurs points clefs du plan en coupe de la pyramide. Ses résultats, basés selon lui sur des tracés géométriques simples[16] peuvent paraître compliqués pour le néophyte et il demeure impossible de vérifier s'il s'agit de simples coïncidences ou bien des réelles intentions de l'architecte.

  • Chambre du roi. Le niveau du sol se situe à 82 coudées. Le niveau des points d'intersection F et E des conduits avec le revêtement de la pyramide est à 154 coudées. La distance entre F et E vaut 2×(220 – 154×11/14) = 198 coudées, valeur de BG (distance entre le sommet de la pyramide et le sol de la chambre du roi). La diagonale du plan du niveau de la chambre du roi vaut 2×(220 – 82×11/14):sin(45°) = 440 coudées, valeur des côtés de la base de la pyramide. Le conduit nord à une pente de 7/11, valeur de la pente de la diagonale EL d'un rectangle ayant comme hauteur la distance du sommet de la pyramide jusqu'à l'intersection des conduits (126 coudées) et comme base 198 coudées.
  • Inclinaisons des conduits. Soit le carré CJKA de 280 coudées de côtés. Le point F est le point d'intersection de la diagonale de ce carré avec le cercle de rayon CJ. Ce point F se trouve à 280×sin(45°) = 198 coudées sous le sommet soit à 82 coudées du sol, donc au niveau de la chambre du roi. Soit le carré BDGH de 198 coudées de côté. Les points d'intersection F et E du carré avec le revêtement de la pyramide déterminent l'emplacement des extrémités des conduits.
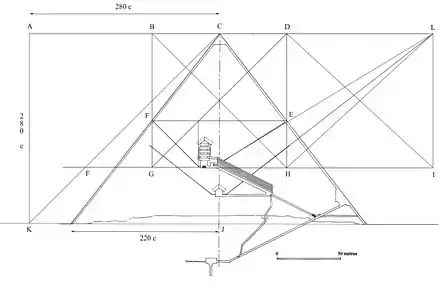
Géométrie des conduits de ventilation (selon John Legon).

La chambre du roi
Géométrie de la chambre du roi.

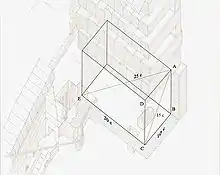
Les dimensions au sol de la chambre du roi sont de 20 × 10 coudées. Sa hauteur est de 11,172 coudées[17]. L'égyptologue Jean-Philippe Lauer montre que cette dernière valeur fut obtenue avec le triangle rectangle ABC obtenu avec la diagonale du côté ABCD de la chambre (voir figure ci-contre). Cette diagonale correspond à un chiffre entier de quinze coudées. Par conséquent, la valeur de la hauteur AB est égale à 11,18 coudées (valeur proche à 0,01 coudée près) de la mesure effectuée dans la chambre[18]. L'égyptologue remarqua également que cette diagonale AC de 15 coudées implique une diagonale du parallélépipède rectangle de la chambre de vingt-cinq coudées[19]. Le triangle ACE possède ainsi les mêmes proportions que le triangle sacré égyptien dont les côtés valent trois, quatre et cinq coudées. Cette chambre possède également la particularité d'être située au niveau où la surface au sol de la pyramide est égale à la moitié de la surface de sa base (observation détaillée dans le paragraphe Relations de surfaces).

Critique de ces théories

En 1988, dans Le Pendule de Foucault, puis dans un ouvrage de 1990 intitulé Les Limites de l'Interprétation, l'écrivain Umberto Eco tourne en dérision l'interprétation à outrance des faits avérés ou légendaires de l'histoire. Il tire des dimensions d'un kiosque à journaux pris au hasard dans sa rue, le même genre d'informations et d'analyses que celles faites parfois sur la pyramide de Khéops. Il montre ainsi que lorsqu'on s'applique à essayer de trouver des nombres remarquables comme Pi, ou la distance de la Terre à la Lune, on peut les trouver facilement, même dans un objet du quotidien.

Références bibliographiques
  • (en) William Matthew Flinders Petrie, The Pyramids and Temples of Gizeh,
  • André Pochan, L'Énigme de la grande pyramide,
  • Jean-Philippe Lauer, Le Mystère des pyramides, (ISBN 978-2-258-02368-0)
  • Gilles Dormion, La Chambre de Chéops,
  • (de) Armin Wirsching, Die Pyramiden von Giza : Mathematik in Stein gebaut, Norderstedt, Books on Demand, rééd. 2009, 2e éd., 124 p., poche (ISBN 978-3-8370-2355-8)
  • Revue Scriba, « Les conduits d'aération de la grande pyramide de Giza », no 4, 1995
  • (en) Alexandre Badawy, « The stellar destiny of pharaoh and the so-called air-shafts in Cheops' pyramid », MIOAWB 10, 1964, p. 189-206
  • (en) Robert Bauval, « The star-shafts of Cheops'pyramid », Discussions in Egyptology, n° 29, 1994, p. 25-27
  • (en) John Legon, « Air-shafts alignments in the great pyramid », Discussions in Egyptology, n° 28, 1994, p. 30-34
  • (en) John Legon, « The orion correlation and the air-shafts theories », Discussions in Egyptology, n° 33, 1995, p. 45-56

Articles connexes

Notes
  1. Lauer 1988, p. 234.
  2. Lauer 1988, p. 232.
  3. Selon R. P. Hypher, « The Value of " pi " and the Pyramids of Egypt. Intentional or Accident?», The Journal of the Society for the Study of Egyptian Antiquities, (ISSN 0383-9753), 1978, vol. 8, no 4, « la valeur de π apparaissant dans la relation entre la hauteur et la longueur de la pyramide est vraisemblablement co-accidentelle ».
  4. 43 mètres, Dormion 2004, Planche 2.
  5. Donnée par la formule 2πR.
  6. Petrie 1883, extrait de Iorwerth Eiddon Stephen Edwards, Les Pyramides d'Égypte, 1992 (ISBN 9782253058632), p. 316.
  7. (en) Mark Lehner, The Complete Pyramids, 1997, p. 109.
  8. Il est aisé de vérifier ce fait en téléchargeant un logiciel gratuit d'astronomie permettant d'afficher la position des étoiles en fonction de la date entrée. On vérifie ainsi qu'en -2650, l'étoile alpha du dragon avait un azimut de 0°53'.
  9. Sous l'impulsion d'Alexandre Badawy, Scriba, Les conduits d'aération de la grande pyramide de Giza, no 4, 1995, p. 93-101.
  10. Dormion 2004, p. 278.
  11. Dormion 2004, p. 205.
  12. Calculé avec le logiciel Cartes du ciel v.2.76 (-2650BC aux latitudes et longitudes de la grande pyramide).
  13. Dormion 2004, p. 144.
  14. L'angle formé entre ces conduits et les faces de la pyramide est presque droit : 90° 18' 34" pour le conduit sud et 89° 18' 34" pour le conduit nord.
  15. (en) « Site de John Legon ».
  16. Scriba, no 4, 1995, p. 98-99.
  17. Lauer 1988, p. 236.
  18. Pour retrouver cette mesure, il faut appliquer le théorème de Pythagore.
  19. Toujours Pythagore appliqué au triangle rectangle ACE.
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.