Objet projectif

Un objet ${\displaystyle P}$ dans une catégorie ${\displaystyle {\mathcal {C}}}$ est dit projectif si pour tout épimorphisme ${\displaystyle e:E\twoheadrightarrow X}$ et tout morphisme ${\displaystyle f:P\to X}$, il existe un morphisme ${\displaystyle {\overline {f}}:P\to E}$ tel que ${\displaystyle e\circ {\overline {f}}=f}$, c'est-à-dire que le diagramme suivant commute :

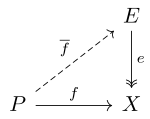
Autrement dit, tout morphisme ${\displaystyle P\to X}$ se factorise par les épimorphismes ${\displaystyle E\twoheadrightarrow X}$[1].

Si C est localement petite, et donc qu'en particulier ${\displaystyle \operatorname {Hom} _{C}(P,X)}$ est un ensemble pour tout objet X de C, cette définition est équivalente à dire que le foncteur hom (également appelé foncteur coreprésentable) :

${\displaystyle \operatorname {Hom} (P,-)\colon {\mathcal {C}}\to \mathbf {Set} }$

préserve les épimorphismes[2].

• Le coproduit de deux objets projectifs est projectif[3].
• La rétraction d'un objet projectif est projective[4].

L'affirmation que tous les ensembles sont projectifs est équivalente à l'axiome du choix[5].

Les objets projectifs de la catégorie des groupes abéliens sont les groupes abéliens libres.

Soit ${\displaystyle R}$ un anneau, et ${\displaystyle R}$- Mod la catégorie (abélienne) des${\displaystyle R}$ -modules à gauche. Les objets projectifs de ${\displaystyle R}$ - Mod sont exactement les modules projectifs. Par conséquent, ${\displaystyle R}$ est lui-même un objet projectif dans ${\displaystyle R}$ - Mod. De manière duale, les objets injectifs dans ${\displaystyle R}$ - Mod sont exactement les modules injectifs.

La catégorie des ${\displaystyle R}$ -modules à gauche (resp. à droite) a de plus suffisamment de projectifs. C'est le cas, car pour tout ${\displaystyle R}$ -module à gauche (resp. à droite) ${\displaystyle M}$, on peut considérer ${\displaystyle F}$ le module libre (et donc projectif) engendré par un ensemble ${\displaystyle X}$ qui est générateur pour ${\displaystyle M}$ (on peut en réalité prendre ${\displaystyle X}$ égal à ${\displaystyle M}$). La projection canonique ${\displaystyle \pi \colon F\to M}$ est la surjection requise.

Dans la catégorie des espaces de Banach munis des contractions, les épimorphismes sont exactement les fonctions dont l'image est dense. Wiweger (1969) montre que l'espace nul est le seul objet projectif de cette catégorie. Il existe cependant des espaces non triviaux et projectifs par rapport à la classe des contractions surjectives. Dans la catégorie des espaces vectoriels normés munis des contractions (et des fonctions surjectives comme "surjections"), les objets projectifs sont exactement les espaces ${\displaystyle l^{1}}$[6] :

${\displaystyle l^{1}(S)=\{(x_{s})_{s\in S},\sum _{s\in S}\|x_{s}\|<\infty \}.}$