Masse d'air (énergie solaire)

Le rayonnement solaire suit étroitement celui du corps noir à 5 800 K[1]. Ce rayonnement est cependant atténué par diffusion et absorption en traversant l'atmosphère terrestre : plus l'épaisseur de celle-ci est grande, plus cette atténuation est sensible. Certains gaz de l'atmosphère absorbent des longueurs d'onde spécifiques, qui sont très fortement atténuées dans le rayonnement solaire parvenant au sol : c'est le cas de la vapeur d'eau, qui absorbe plusieurs longueurs d'onde, ainsi que de l'azote, de l'oxygène et du dioxyde de carbone. Le spectre solaire au niveau du sol est ainsi étroitement restreint aux longueurs d'onde comprises entre l'infrarouge lointain et le proche ultraviolet.

• 
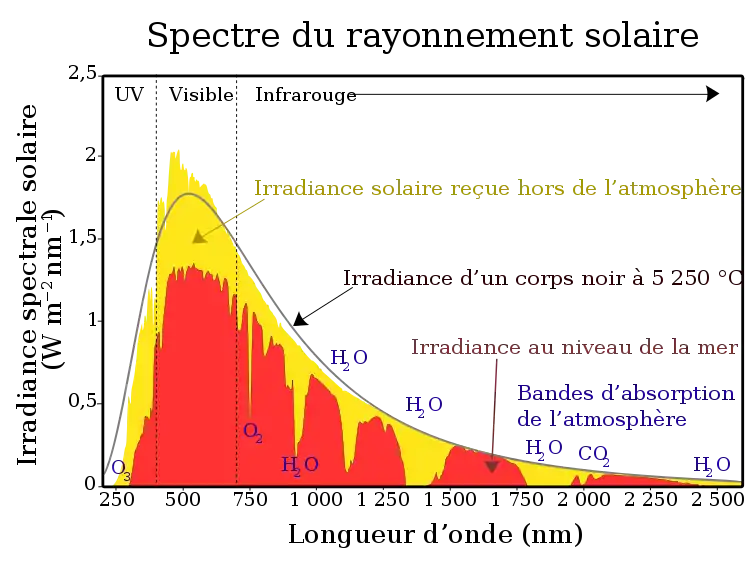
  Rayonnement solaire au niveau de la mer et au-dessus de l'atmosphère indiquant les différentes raies d'absorption des gaz atmosphériques.

Outre les phénomènes d'absorption spectrale, les molécules des gaz de l'atmosphère dispersent également la partie basse — dans le bleu — des longueurs d'onde du rayonnement solaire par diffusion élastique avec les photons incidents, dite diffusion de Rayleigh dans ce cas, phénomène responsable de la couleur du ciel, tandis que le soleil paraît plus jaune, couleur complémentaire du bleu sur le cercle chromatique. Plus l'épaisseur d'atmosphère traversée par le rayonnement solaire est grande, plus l'effet de la diffusion de Rayleigh est sensible : c'est la raison pour laquelle le soleil paraît de plus en plus rouge à mesure qu'il décline sur l'horizon, car sa lumière perd une fraction de plus en plus importante de bleu dans son spectre.

Si ${\displaystyle L}$ est le chemin optique du rayonnement solaire et ${\displaystyle L_{\mathrm {o} }}$ le chemin optique au zénith au niveau de la mer alors le coefficient de masse d'air vaut[2] :

${\displaystyle AM={\frac {L}{L_{\mathrm {o} }}}}$.

Ce coefficient dépend donc de la hauteur du Soleil sur l'horizon ainsi que de l'altitude et la latitude de l'observateur, et varie tout au long de la journée ainsi que selon les saisons.

Si ${\displaystyle z}$ est la distance zénithale du Soleil exprimée en degrés, on peut écrire en première approximation, qui reste raisonnable jusqu'à une hauteur d'environ 15° au-dessus de l'horizon — car la fomule ignore la courbure de la Terre et tend donc vers l'infini lorsque le Soleil se rapproche de l'horizon :

${\displaystyle AM\approx \sec z={\frac {1}{\cos \ z}}}$.

De nombreux développements ont été proposés pour décrire de manière plus précise la masse d'air près de l'horizon, comme le modèle Kasten & Young en 1989[3] :

${\displaystyle AM={\frac {1}{\cos z+0,50572\,(96,07995-z)^{-1,6364}}}}$.

Il en existe de nombreux autres. Au niveau de la mer, la masse d'air à l'horizon vaut par exemple 37,9 avec le modèle de Kasten & Young, mais 40 selon celui de G. V. Rozenberg en 1966[4] :

${\displaystyle AM={\frac {1}{\cos z+0,025\,e^{-11\cos z}}}}$.

Si ${\displaystyle R_{\mathrm {T} }}$ est le rayon de la Terre et ${\displaystyle h_{\mathrm {atm} }}$ la hauteur effective de l'atmosphère, on peut modéliser avec une bonne approximation l'atmosphère terrestre comme une enveloppe sphérique simple de ${\displaystyle h_{\mathrm {atm} }}$ = 9 km de hauteur effective autour d'une planète de ${\displaystyle R_{\mathrm {T} }}$ = 6 371 km de rayon, on peut écrire leur rapport ${\displaystyle r=R_{\mathrm {T} }/h_{\mathrm {atm} }\approx 708}$ et l'appliquer à la formule générale[5] :

${\displaystyle AM={\sqrt {(r\cos z)^{2}+2r+1}}\;-\;r\cos z}$.

• 
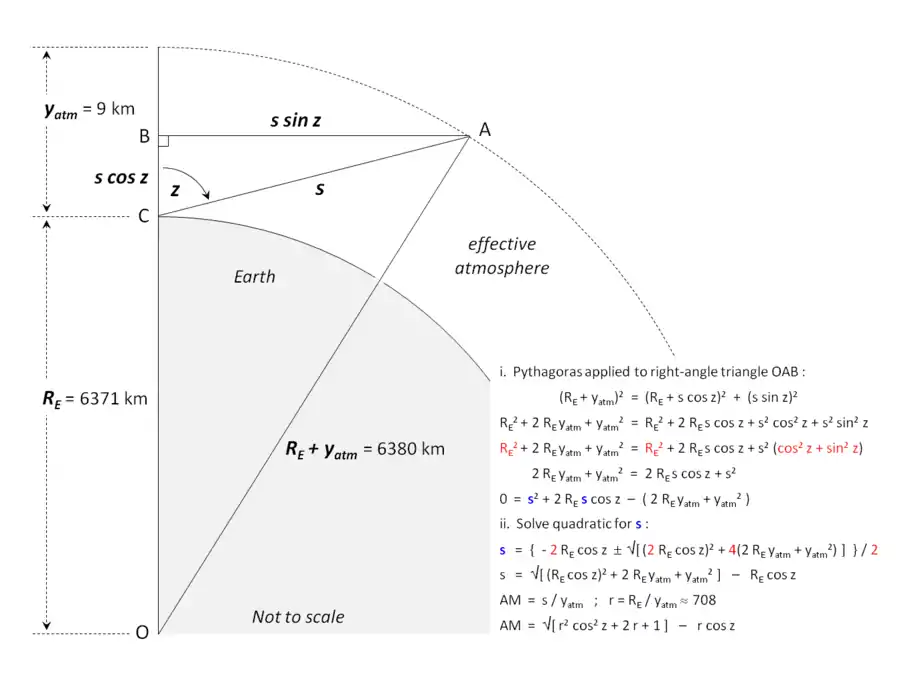
  (en) L'effet de l'atmosphère terrestre sur la transmission du rayonnement solaire jusqu'au sol peut être modélisé comme si l'atmosphère était concentrée dans un volume limité à 9 km d'altitude.

Le tableau ci-dessous donne une comparaison de ces différents modèles à différentes distances zénithales :

Valeurs approchées du coefficient de masse d'air au niveau de la mer.

${\displaystyle z}$	Terre plate	Kasten et Young[3]	Rozenberg[4]	Sphère[5]
0°	1,0	1,0	1,0	1,0
60°	2,0	2,0	2,0	2,0
70°	2,9	2,9	2,9	2,9
75°	3,9	3,8	3,8	3,8
80°	5,8	5,6	5,6	5,6
85°	11,5	10,3	10,3	10,6
88°	28,7	19,4	19,3	20,3
90°	${\displaystyle \infty }$	37,9	40,0	37,6

Cela signifie que, pour cette application, l'atmosphère peut être considérée comme concentrée jusqu'à une altitude de 9 km, de sorte que tous les effets de l'atmosphère sont considérés provenir de la moitié inférieure de la troposphère. Il s'agit d'un modèle approché simple et utile pour les calculs relatifs à l'intensité de l'énergie solaire à la surface de la Terre.

Les valeurs de coefficients de masse d'air ci-dessous sont celles auxquelles il est le plus souvent fait référence.

• AM0

Il s'agit du rayonnement solaire au-dessus de l'atmosphère terrestre — littéralement « zéro atmosphère » — correspondant grossièrement au rayonnement d'un corps noir à 5 800 K. C'est le standard utilisé pour les applications spatiales, par exemple pour les nombreux satellites en orbite terrestre basse tels que la station spatiale internationale. À ce niveau, l'irradiation solaire totale reçue par unité de surface correspond à la constante solaire et vaut 1 360,9 ± 0,5 W/m²[6].

• AM1

Il s'agit du rayonnement solaire reçu au niveau de la mer avec un soleil au zénith, correspondant littéralement à une épaisseur d'atmosphère terrestre. L'intervalle de coefficients AM1 (${\displaystyle z}$ = 0°) et AM1.1 (${\displaystyle z}$ = 25°) est celui qu'on retient pour les applications solaires au niveau de la mer dans les régions équatoriales ou tropicales.

• AM1.5

Ce coefficient est celui généralement retenu pour les applications solaires dans les régions tempérées. Il correspond à une distance zénithale de 48,2°. On le rencontre souvent écrit AM1.5G, le « G » signifiant « global » et indiquant qu'on considère le rayonnement direct du soleil et le rayonnement diffusé par le ciel. L'irradiation correspondant au spectre AM1.5G est de l'ordre de 970 W/m², ce qu'on arrondit généralement à 1 000 W/m² pour simplifier les calculs avant prise en compte des divers effets d'atténuation qui affectent le rayonnement reçu ; la composante directe seule, sans la diffusion atmosphérique, est de l'ordre de 887 W/m²[7].

• AM2 à AM3

Les coefficients AM2.0 (${\displaystyle z}$ = 60°) à AM3.0 (${\displaystyle z}$ = 70°) s'appliquent aux latitudes élevées, par exemple subarctiques. En pratique, le coefficient AM2.0 est pratique pour calculer la performance d'une installation en hiver, dans la mesure où la masse d'air reste supérieure à 2 toute la journée aux alentours du solstice d'hiver aux latitudes voisines de 37° et au-delà, ce qui est par exemple le cas de Tunis.

L'intensité du rayonnement reçu décroît lorsque le coefficient de masse d'air croît, mais cette évolution n'est pas linéaire car de multiples facteurs atmospéhriques entrent en ligne de compte. Ainsi, l'essentiel des longueurs d'onde énergétiques est éliminé dans la haute atmosphère, de sorte que l'énergie reçue avec un coefficient AM2 n'est pas moitié moindre que celle reçue avec un coefficient AM1, et donc un soleil au zénith[8]. De plus, l'humidité atmosphérique et la présence d'aérosols, de smog photochimique voire d'une couche d'inversion peuvent atténuer le rayonnement jusqu'à près de 70 % à proximité de l'horizon.

Si l'on écrit ${\displaystyle I_{\mathrm {0} }}$ = 1 353 W/m² la constante solaire reçue au sol, une approximation couramment employée pour déterminer l'intensité du rayonnement reçu en fonction de la masse d'air peut s'écrire[9] - [10] :

${\displaystyle I_{\mathrm {G} }=1,1\times I_{\mathrm {0} }\times 0,7^{AM^{0,678}}}$.

Le facteur 1,1 vient de ce qu'on estime généralement que la composante diffusée du rayonnement reçu représente 10 % de sa composante directe, d'où ${\displaystyle I_{\mathrm {G} }=1,1\times I_{\mathrm {D} }}$, tandis que le facteur 0,7 provient du fait qu'environ 70 % de l'intensité incidente est transmise par l'atmosphère terrestre jusqu'au sol ; l'exposant 0,678 est empirique et tient compte des propriétés non uniformes des couches de l'atmosphère. Cette formule s'inscrit dans l'incertitude découlant des facteurs atmosphériques variables tels que la pollution :

Intensité ${\displaystyle I_{\mathrm {G} }}$ en fonction de l'angle ${\displaystyle z}$ et du coefficient AM.

${\displaystyle z}$	AM	Effet de la pollution	Valeur calculée	ASTM G-173[11]
—	0	1 367[alpha 1]	1 353	1 347,9[alpha 2]
0°	1	840 .. 1 130 = 990 ± 15 %	1 040
23°	1.09	800 .. 1 110 = 960 ± 16 %[alpha 3]	1 020
30°	1.15	780 .. 1 100 = 940 ± 17 %	1 010
45°	1.41	710 .. 1 060 = 880 ± 20 %[alpha 3]	950
48,2°	1.5	680 .. 1 050 = 870 ± 21 %[alpha 3]	930	1 000,4[alpha 4]
60°	2	560 .. 970 = 770 ± 27 %	840
70°	2.9	430 .. 880 = 650 ± 34 %[alpha 3]	710
75°	3.8	330 .. 800 = 560 ± 41 %[alpha 3]	620
80°	5.6	200 .. 660 = 430 ± 53 %	470
85°	10	85 .. 480 = 280 ± 70 %	270
90°	38		20

Ce tableau illustre le fait que l'intensité disponible pour les applications solaires ne décroît sensiblement qu'à l'approche de l'horizon : l'intensité du rayonnement reçu atteint encore 60 % de sa valeur maximale quand le soleil n'est plus qu'à 15° de l'horizon.

L'intensité reçue croît avec l'altitude puisque la masse d'air traversée par le rayonnement solaire diminue. Si ${\displaystyle AM}$ est la masse d'air calculée au niveau de la mer alors l'intensité reçue à l'altitude ${\displaystyle h}$ exprimée en kilomètres au-dessus du niveau de la mer peut être exprimée à partir de ${\displaystyle I_{\mathrm {0} }}$ = 1 353 W/m² par l'équation[10] - [12] :

${\displaystyle I=1,1\times I_{\mathrm {0} }\times [\,(1-a\,h)\,0,7^{AM^{0,678}}+a\,h]}$

Le coefficient ${\displaystyle a}$ vaut environ 0,14 dans cette formule, qui ne s'applique qu'aux quelques premiers kilomètres au-dessus du niveau de la mer.