Constante solaire

Le rayonnement du Soleil émis par la chromosphère peut être modélisé par celui d'un corps noir. Pour ce faire, on considère que la température de surface est ${\displaystyle T_{\odot }}$ de 5 780 K environ. Il produit une émittance ${\displaystyle F_{\odot }}$ quantitativement estimable par la loi de Stefan-Boltzmann :

${\displaystyle F_{\odot }=\sigma T_{\odot }^{4}=63,2\;{\textrm {MW}}\cdot {\textrm {m}}^{-2}}$.

À une distance R, en posant la conservation de l'énergie rayonnée à travers l'espace, il vient que :

${\displaystyle 4\pi R_{\odot }^{2}F_{\odot }=4\pi R^{2}F}$

${\displaystyle F=F_{\odot }\left({\frac {R_{\odot }}{R}}\right)^{2}}$.

où ${\displaystyle R_{\odot }}$ est le rayon solaire, égal à 696 342 km.

L'application numérique donne :

${\displaystyle \ F=\left({\dfrac {5\ 535.8}{R}}\right)^{2}}$

où R s'exprime en millions de kilomètres et F en watts par mètre carré.

Pour la Terre, où R = 1 au = 150 millions de kilomètres, on obtient

${\displaystyle F=1\ 362\;{\textrm {W}}\cdot {\textrm {m}}^{-2}}$.

Variation de la constante solaire entre 1978 et 2003.

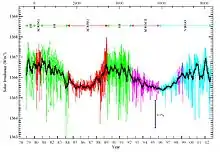
Depuis la formation du Système solaire, il y a environ 4,7 milliards d’années, l’intensité du rayonnement solaire a augmenté. À cette époque, elle ne valait que 70 % de sa valeur actuelle et, pendant le Carbonifère, il y a environ 300 millions d’années, elle était environ 2,5 % moins élevée qu’aujourd’hui.

La constante solaire, exprimée comme pourcentage de sa valeur actuelle, peut se décrire par l’équation suivante (le temps t étant exprimé en milliards d’années depuis l’apparition du système solaire) :

${\displaystyle \left[1+0,4\left(1-{\frac {t}{4,7}}\right)\right]^{-1}}$.

Ainsi, dans 4,7 milliards d’années, le Soleil serait environ 67 % plus puissant que maintenant, par son rayonnement émis. De possibles variations temporaires d’une durée de 10 millions d’années (tous les 300 millions d’années environ) pourraient expliquer les périodes glaciaires sur Terre : le Pléistocène est une période glaciaire, les précédentes se sont produites il y a 300 et 700 millions d’années. Mais d'autres effets terrestres seraient prépondérants, comme la disposition des continents (autour des pôles) ou la concentration des gaz à effet de serre.

La constante solaire varie, de l’ordre de 1 à 5 W/m², sur des échelles de temps plus courtes, de quelques jours à quelques années, par exemple en raison de la présence ou de l’absence de taches solaires ou de l’activité solaire.

Évolution de la température terrestre moyenne, de la concentration de CO₂ et du nombre taches solaires depuis 1850.

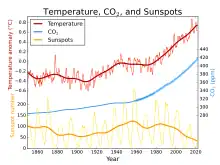
Sur le long terme, la position astronomique de la Terre par rapport au Soleil est le principal facteur de variabilité naturelle de la température globale, au travers de la « constante » solaire.

Les cycles principaux concernent :

• les variations de l’excentricité de l’orbite terrestre (cycle actuel de 100 000 ans) ;
• l’obliquité de l'axe des pôles (cycle actuel d’environ 41 500 ans) ;
• la précession des équinoxes ;
• l’activité solaire, qui fluctue selon un cycle de 11 ans, caractérisé par le nombre de taches solaires.

Parmi ces quatre facteurs, seuls le premier et le quatrième modifient la valeur de l'irradiance solaire reçue par la Terre. Les deux autres facteurs modifient la distribution de l'énergie solaire sur la surface terrestre, mais pas l'irradiance.

L'intégration de tous ces facteurs et d'autres dans le cadre la théorie astronomique des paléoclimats a donné lieu à des travaux divers en climatologie et cyclostratigraphie.

La première détermination sérieuse de la constante solaire date de 1838 et revient à Claude Pouillet qui l'estime à 1 228 W m⁻². Cette valeur, pourtant proche de la réalité, est remise en question en 1881 par Samuel Pierpont Langley qui trouve une constante égale à 2 140 W m⁻² à la suite d'une expédition au sommet du mont Whitney (4 420 m). Cette valeur fera référence pendant plus de 20 ans[12].

Il aura fallu attendre la mise en orbite de radiomètres modernes pour affiner cette mesure. En 1978, le radiomètre HF sur le satellite Nimbus 7 annonce une valeur de 1 372 W/m². Cette valeur est rapidement corrigée à 1 367 W/m² par ACRIM I sur SMM. Plus récemment, VIRGO sur SoHO ramène cette valeur à 1 365,4 ± 1,3 W m⁻² en 1998[13].

La valeur admise depuis 2008 est égale à 1 360,8 ± 0,5 W m⁻²[1].