Méthode de la zone fondue
La méthode de la zone fondue (également appelée technique de la zone fondue, fusion de zone ou raffinage par zone fondue et désignée en anglais par les termes zone melting et zone refining) est une technique permettant de purifier des composés cristallisés stables à la fusion. L'avantage de cette technique est qu'elle peut permettre d'obtenir de très hauts degrés de pureté (99,999 % en masse pour le silicium[1], par exemple). Elle a été inventée dans les années 1950 par W. G. Pfann[2].


(Image de droite) zone fondue vertical, en 1961. la bobine de chauffage par induction est traversée par un courant alternatif à haute fréquences, elle fait fondre une section de la barre de métal dans le tube. La bobine se déplace lentement vers le bas du tube, déplaçant la zone fondue vers l'extrémité de la barre.
La méthode est principalement appliquée aux métaux, semi-conducteurs, ou autres composés inorganiques (oxydes, intermétalliques, etc.)[3]. Quelques applications existent pour les composés organiques[4], mais elles restent toutefois peu nombreuses en raison de leur faible stabilité à l'état fondu.
Le phénomène physicochimique sur lequel se fonde la méthode existe dans la nature[5], mais de façon extrêmement limitée.
Principe de la technique
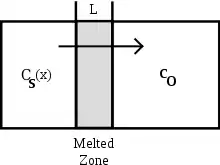



La fusion de zone consiste à générer une zone fondue sur un échantillon de solide à purifier (appelé "lingot"), et à déplacer de façon très lente cette zone d'une extrémité à l'autre du lingot. L'échantillon à purifier présente généralement une géométrie cylindrique ou parallélépipédique.
Selon la différence de solubilité des impuretés de l'échantillon entre la phase fondue et la phase solide, elles peuvent être déplacées aux différentes extrémités du lingot. À chaque déplacement élémentaire de la zone fondue, la fraction élémentaire de solide qui recristallise présente une concentration en impureté différente de la phase fondue, d'où la possibilité de déplacer les impuretés dans l'échantillon grâce au déplacement de la zone liquide.
Généralement, un passage unique de zone fondue ne permet pas d'obtenir une purification intéressante pour les applications visées. Néanmoins, des passages répétés permettent d'accentuer le phénomène de concentration des impuretés aux extrémités du lingot, permettant de rendre la partie centrale de l'échantillon beaucoup plus pure.
Dans les échantillons inorganiques, la zone fondue est généralement créée par induction électromagnétique ou chauffage laser/infrarouge. Pour les échantillons organiques, le lingot est généralement fondu et re-solidifié dans un tube cylindrique de verre amorphe ou cristallin. La zone fondue est ainsi souvent générée par une résistance électrique annulaire qui entoure le cylindre.
Thermodynamique et cinétique
Aspect thermodynamique
La thermodynamique, plus particulièrement les diagrammes de phases entre le composé à purifier et ses impuretés, aide à comprendre le fonctionnement du procédé et à prévoir son efficacité. Plusieurs comportements d'impuretés peuvent être distingués.
Impuretés abaissant le point de fusion
Une impureté qui abaisse le point de fusion implique, sur le diagramme de phases entre le composé à purifier et l'impureté, des solidus et liquidus décroissants avec augmentation croissante de l'impureté dans le système. Ainsi, à concentration donnée d'impureté dans la phase liquide, la phase solide qui recristallise présente une concentration plus faible en impureté que la zone fondue.
Ces impuretés sont donc déplacées dans le même sens que la zone fondue.
Impuretés augmentant le point de fusion
Une impureté qui augmente le point de fusion implique, sur le diagramme de phases entre le composé à purifier et l'impureté, des solidus et liquidus croissants avec augmentation croissante de l'impureté dans le système. Ainsi, à concentration donnée d'impureté dans la phase liquide, la phase solide qui recristallise présente une concentration plus importante en impureté que la zone fondue.
Ces impuretés sont donc déplacées dans le sens inverse du sens de déplacement de la zone fondue.
Impuretés indifférentes vis-à-vis du point de fusion du solide à purifier
Il peut arriver que certaines impuretés n'abaissent, ni n'augmentent le point de fusion du composé à purifier. Ce cas de figure est relativement restreint : il peut par exemple concerner un système contenant deux énantiomères en solution solide totale et idéale, ou un solide à purifier dont la composition est celle d'un composé à fusion congruente.
Dans ce cas, à chaque déplacement élémentaire de zone fondue, la fraction recristallisée présente la même concentration en impureté que la zone. La fusion de zone devient ainsi une technique non-pertinente pour purifier le solide considéré.
Bien qu'il soit rare de trouver de tels cas de figure, il est possible de trouver des situations qui s'en rapprochent. Si une impureté abaisse ou augmente le point de fusion du composé à purifier, mais que les courbes de liquidus et de solidus sont très proches l'une de l'autre, la fusion de zone n'est pas la technique la plus adaptée à la purification du composé.
Aspect cinétique
La vitesse de déplacement de la zone fondue présente une importance notable pour l'efficacité du procédé. L'efficacité maximale théorique de la technique est obtenue pour une vitesse de déplacement qui tend vers zéro. À l'inverse, plus la vitesse est rapide, moins l'efficacité est bonne (jusqu'à devenir nulle).
Modélisation de la redistribution d’une impureté par fusion de zone
Il est possible de prédire le profil de distribution d’une impureté après fusion de zone moyennant quelques hypothèses. Toutefois, les équations différentielles permettant cela ne présentent pas toutes des solutions analytiques ; il est donc nécessaire d’employer des méthodes graphiques ou numériques afin de les résoudre.
Notations et hypothèses
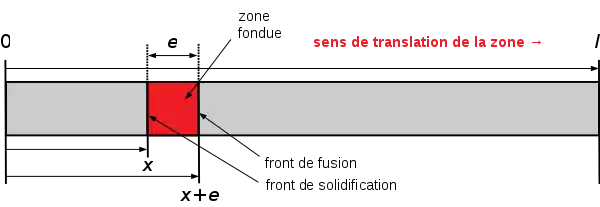
On considère un lingot cylindrique droit de solide impur présentant une teneur massique en impureté. Sa longueur vaut et sa section droite, supposée constante, . Le lingot est raffiné avec une zone cylindrique droite de longueur maintenue constante, à vitesse de translation constante (voir schéma ci-dessus). On désigne par :
- : la position du front de solidification dans le lingot ().
- : la teneur massique fractionnaire en impureté dans la tranche de solide redéposée à la position après le passage de zone fondue de rang ().
- : la teneur massique fractionnaire en impureté dans la zone fondue lorsque le front de solidification se trouve à la position au passage de rang ().
- et : les masses volumiques des phases solide et liquide (fondue).
On cherche à exprimer , la teneur du lingot en impureté quels que soient la position dans le lingot et le rang du passage de zone fondue. Pour cela, on introduit une grandeur utile : le coefficient de ségrégation de l’impureté, qu’on peut supposer dépendre, dans un cas général, de la composition de la zone fondue (donc, de la position de la zone et du rang du passage), et qu’on note par conséquent . Ce coefficient traduit le rapport entre la composition de la tranche de solide déposée au front de solidification de la zone à un instant donné, et celle de la zone : .
Pour résoudre ce problème, il est nécessaire de réaliser deux bilans de matière distincts : en effet, tant que le front de fusion n’a pas atteint l’extrémité finale du lingot (), la zone subit une entrée de matière permanente puisqu’elle incorpore une tranche de solide au front de fusion à chacun de ses déplacements élémentaires. Ceci n’est en revanche plus vrai lorsque le front de fusion a atteint la longueur du lingot ().
Dans la région
À chaque déplacement élémentaire de la zone, la masse d’impureté incorporée à la zone au front de fusion est . La masse d’impureté rejetée dans la tranche de solide redéposée au front de solidification est . La masse d’impureté accumulée dans la zone s’écrit quant à elle . En supposant que les densités des phases liquide et solide sont identiques, le principe de conservation de la matière implique l’égalité suivante :
On peut alors utiliser la définition du coefficient de ségrégation, , pour réexprimer en fonction de . On obtient alors , ce qui aboutit à l’équation différentielle suivante :
Pour chaque passage de zone de rang , la condition initiale est donnée par :
Si le coefficient de ségrégation et la longueur de zone sont supposés constants tout le long du procédé (on note ainsi ), il existe alors des expressions analytiques de la condition initiale et du profil de distribution de l’impureté dans la région pour le premier passage de zone fondue :
Dans la région
Lorsque le front de fusion atteint le haut du lingot, il n’y a plus d’entrée de matière dans la zone et la longueur de cette dernière diminue au fur et à mesure qu’elle avance (). À chaque déplacement de la zone, une tranche de liquide contenant d’impureté en masse se scinde en deux parties : l’une s’incorpore à la tranche de solide déposée au front de solidification et contient en masse d’impureté, et l’autre contribue à l’accumulation d’impureté dans la zone à hauteur d’une masse de . En supposant que , la conservation de la matière donne donc l’égalité qui suit :
En utilisant la définition du coefficient de ségrégation, cette équation devient :
La condition initiale de cette équation est la valeur de la teneur du lingot en impureté en , qu’on calcule à l’aide de l’équation différentielle établie dans la partie précédente. Si le coefficient de ségrégation est supposé constant, l’équation présente une solution analytique valable quel que soit le rang du passage de zone :
Résolution numérique des équations différentielles
L’une des méthodes consistant à résoudre numériquement les équations différentielles permettant de déterminer le profil de distribution d’une impureté après raffinage par zone fondue est de discrétiser le lingot en intervalles les plus petits possibles.
Pour chaque passage de rang , la teneur en impureté du lingot en se calcule grâce à l’équation suivante :
Pour le premier passage de zone fondue, .
Pour chaque passage, la composition de la tranche déposée en vaut :
Ces calculs peuvent être mis en œuvre grâce à un simple tableur, ou un logiciel de calcul type Scilab/Matlab/GNU Octave.
Limites de la technique
La fusion de zone ne peut être utilisée dans les cas suivants :
- Impureté à retirer indifférente vis-à-vis du point de fusion du composé à purifier
- Composé à purifier instable à la fusion (ce qui concerne principalement les composés organiques, ou les composés intermétalliques à fusion non-congruente).
Applications
La méthode est utilisée pour produire des quantités relativement faibles de métaux ultra-purs : fer, titane, zirconium, wafer de silicium destiné à l'industrie électronique, et pour des utilisations principalement en:
- électronique
- photovoltaïque
- fabrication de matériaux de référence certifiés
Notes et références
- P. R. Mei, S. P. Moreira, E. Cardoso et A. D. S. Côrtes, « Purification of metallurgical silicon by horizontal zone melting », Solar Energy Materials and Solar Cells, vol. 98, , p. 233-239 (DOI 10.1016/j.solmat.2011.11.014, lire en ligne, consulté le )
- « US2739088.pdf », sur docs.google.com (consulté le )
- (en) Peter O. Hahn, « Sand and Silicon. Science that Changed the World. By Denis McWhan. », Angewandte Chemie International Edition, vol. 51, , p. 12164-12165 (ISSN 1521-3773, DOI 10.1002/anie.201207329, lire en ligne, consulté le )
- (en) William R. Wilcox, Robert Friedenberg et Nathan Back, « Zone Melting of Organic Compounds », Chemical Reviews, vol. 64, , p. 187-220 (DOI 10.1021/cr60228a006, lire en ligne, consulté le )
- (en) Pierre Schiano, Ariel Provost, Roberto Clocchiatti et François Faure, « Transcrystalline Melt Migration and Earth’s Mantle », Science, vol. 314, , p. 970-974 (DOI 10.1126/science.1132485)












































