Loi de mouvement
En génie mécanique, le fonctionnement d'une machine comprend des mouvements dont l'étude peut globalement se résumer aux contraintes suivantes :
- Amener une pièce d'un point A à un point B en une durée T.
Il peut s'agir du trajet d'un outil, d'un capteur ou bien d'une manutention (déplacement d'un objet).
À ce trajet s'ajoutent des contraintes :
- de résistance : les mécanismes doivent être sollicités le moins possible afin d'avoir la durée de vie la plus longue ;
- de consommation : l'énergie dépensée pour ce trajet doit être la plus basse possible.
D'un point de vue mathématiques, il s'agit d'un problème d'optimisation.
Une loi de mouvement est une équation décrivant la manière dont doit se faire le mouvement.
D'un point de vue formel, la position et l'orientation d'une pièce dans l'espace est décrite par un vecteur X de dimension 6 ; dans un repère cartésien, les six composantes sont les trois coordonnées d'un point de la pièce et les trois angles d'Euler. La loi de mouvement est donc de la forme
- X = ƒ(t).
le paramètre t étant le temps. Il peut s'agir d'un fonction analytique ou bien d'une suite discrète de valeurs ((X0, t0), (X1, t1)…, (Xn, tn)), un automate étant chargé de s'assurer que la pièce « soit au rendez-vous » des différents points.
La dérivation, analytique ou numérique, de cette fonction donne accès aux fonctions vecteurs vitesse et vitesse angulaire, accélération et accélération angulaire, à-coup et à-coup angulaire. À l'inverse, cette fonction X étant la primitive des fonctions précédentes, on peut l'obtenir par intégration d'une fonction vitesse ou accélération ou à-coup choisie a priori.
Par la suite, pour des raisons de simplification et sauf mention contraire, nous considérons que le mouvement est une translation rectiligne selon un axe x.
Limites physiques
La pièce à déplacer a une inertie ; les différentes pièces du mécanisme également. Outre l'inertie, les différents mouvements rencontrent des oppositions : résistance au glissement (frottement), résistance au roulement, travail mécanique utile (ce pourquoi on utilise l'outil). Le mécanisme doit donc fournir des efforts (principe fondamental de la dynamique, vaincre les résistances) et toutes les pièces doivent résister à ces efforts.
Les paramètres principaux sont :
- les vitesses : les frottements génèrent une chaleur d'autant plus importante que la vitesse est élevée ; il s'agit d'une perte d'énergie d'une part, et d'autre part l'élévation de température peut modifier le comportement de la matière et endommager des pièces ; par ailleurs, l'énergie cinétique à fournir au système est fonction du carré de la vitesse, celle-ci détermine donc la consommation énergétique du système ;
- les accélérations : selon le principe fondamental de la dynamique, les efforts sont proportionnels à l'accélération ; plus l'accélération est élevée, plus les pièces doivent être robustes et plus l'actionneur (moteur, vérin…) doit développer de puissance ;
- les à-coup : ils sont générateurs de vibrations et donc de bruit (nuisance sonore) mais peuvent aussi provoquer le desserrement de vis d'assemblage et un endommagement par fatigue vibrationnelle.
Lorsque les accélérations sont importantes, on ne peut plus négliger la déformation élastique des pièces et les jeux dans les liaisons : cela introduit un décalage entre les deux bouts de la chaîne cinématique, ce qui d'une part rend difficile la maîtrise du mouvement et d'autre part peut générer des efforts imprévus de type « coup de fouet ».
Outre les limites physiques, la conception est également soumise à des « limites mathématiques » : si l'on désire avoir des fonctions analytiques pour pouvoir travailler sur les lois de mouvement et les reproduire, il faut si possible avoir des lois simples. On utilise en général des lois polynomiales — dont des fonctions constantes et affines — et des lois trigonométriques — sinus, cosinus, tangente. La loi finale est en général un assemblage de plusieurs lois (définition par partie).
Phases du mouvement
Le mouvement comprend au moins deux phases : une phase de démarrage et une phase de freinage. Il nécessite parfois une phase de vitesse constante : soit l'amplitude du mouvement est suffisamment importante pour que la vitesse maximale admissible soit atteinte, soit le travail effectué nécessite d'avoir une vitesse constante, comme un usinage (l'outil de coupe doit se déplacer à vitesse constante). Bien sûr, un mouvement peut être plus complexe et nécessiter de multiples phases.
Pilotage du mouvement
Habituellement, le mouvement peut être piloté de deux manières :
- par une came (pilotage mécanique) ;
- par un automate pneumatique ou, plus probablement, électronique.
Dans le cas d'une came, la loi de mouvement détermine le profil de la came.
Dans le cas d'un automate électronique associé à des actionneurs électriques (moteur électrique, vérin électrique), la loi de mouvement détermine la puissance envoyée dans l'actionneur en fonction du temps.
Notons que ce qui nous intéresse, c'est le mouvement de la pièce en question, de l'effecteur (partie de la machine qui effectue la tâche, la fonction). Mais ce que l'on pilote, c'est l'actionneur (partie de la machine qui produit le mouvement). Il peut y avoir des pièces intermédiaires entre l'actionneur et l'effecteur qui transforment le mouvement, l'effecteur ne suit donc pas nécessairement la même loi de mouvement que l'actionneur.
On peut donc prendre le problème sous deux angles :
- soit on définit la loi de mouvement de l'actionneur, parce que c'est ce qui est le plus simple et que les possibilités sont limitées par la technologie ; on détermine ensuite la loi de mouvement suivie par l'effecteur et on vérifie qu'elle est compatible avec le cahier des charges ;
- soit on définit la loi de mouvement de l'effecteur, puisque c'est ce pour quoi la machine est conçue ; la loi servant à piloter l'actionneur est alors déduite de la loi de mouvement de l'effecteur et on vérifie qu'elle est compatible avec le dispositif.
Approche élémentaire
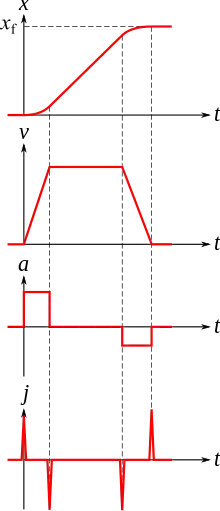
Supposons que l'on doit effectuer un mouvement rectiligne : la pièce en question doit se déplacer d'une abscisse x0 = 0 à une abscisse xf en une durée T, les vitesses initiales et finales étant nulles :
- v(0) = v(T) = 0.
La pièce a donc une vitesse moyenne vmoy = xf/T. Cependant, le mouvement doit avoir une phase d'accélération, la mise en mouvement, puis une phase de freinage.
La première solution qui vient à l'esprit est d'avoir une accélération constante pour amener la pièce jusqu'à une « vitesse de croisière » puis d'avoir une accélération constante pour freiner la pièce jusqu'à l'arrêt. On a donc une loi d'accélération en « marche d'escalier » et une loi de vitesse trapézoïdale. La loi de position est constituée d'un arc de parabole (démarrage) suivi d'une droite (fonction affine) puis d'un arc de parabole (freinage).
Une telle loi n'est pas possible au sens strict : en effet, la discontinuité de l'accélération génère un à-coup infini. L'élasticité du mécanisme va donc limiter la variation de l'accélération d'une part, le mouvement réel aura donc du retard par rapport au mouvement planifié. D'autre part, ce fonctionnement va générer des vibrations importantes.
- La loi de mouvement réelle est nécessairement continue en accélération
c'est-à-dire que la courbe décrivant l'accélération en fonction du temps, a(t), est une fonction continue.
Toutefois, une loi ayant une accélération discontinue n'est pas nécessairement un problème lorsque les vitesses sont faibles. Un automate pneumatique élémentaire fonctionne souvent sur le mode suivant :
- Le distributeur laisse passer l'air jusqu'au vérin.
- Le distributeur se ferme et le circuit se purge.
Lorsque le distributeur s'ouvre, la pression de l'air monte brusquement et provoque une accélération (poussée constante) jusqu'à ce que la vitesse du vérin corresponde au débit de l'air. Lorsque le distributeur de ferme et que le circuit se purge, le vérin arrête de pousser, le système est freiné par frottement et/ou arrêté brusquement par une butée, un amortisseur étant chargé d'amortir le choc.
Prenons le cas d'un manège dont certains éléments peuvent monter avec un élévateur pneumatique. Lorsque l'enfant appuie sur le bouton, le sujet s'élève en se mettant en route de manière « brusque » ; cependant, la vitesse de montée étant faible, l'élasticité du support et la compressibilité de l'air font que l'à-coup ressenti ne provoque pas d'inconfort notable.
Le cas du sujet de manège présente par ailleurs deux différences par rapport à notre cas initial :
- L'actionneur ne se contente pas de mettre une charge en mouvement (donc de vaincre l'inertie), il doit aussi monter une charge (travail utile) ; une fois en position haute, le vérin reste sous pression pour maintenir la charge.
- Si la tige du vérin a un mouvement rectiligne par rapport au corps du vérin, le sujet de manège a lui un mouvement de translation circulaire ; la loi de mouvement que suit l'effecteur (le sujet) n'est donc pas la même que celle de l'actionneur (le vérin).
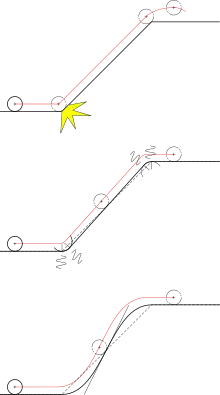 Profils de cames simples Profils de cames simples pour effectuer un mouvement vertical :
|
Si maintenant un mouvement est piloté par une came alors le profil de la came (en noir dans la figure ci-contre) représente la loi de mouvement et sa pente représente la vitesse. Plus précisément, le profil de la came est similaire à la trajectoire du centre du galet (en rouge) et l'abscisse horizontale est proportionnelle au temps si l'on suppose une vitesse de translation vh constante.
Le galet doit donc passer d'une altitude y0 à une altitude yf en une durée T, c'est-à-dire que le galet doit parcourir une distance horizontale vh × T. La première idée consiste donc à tirer une droite entre les points (0 ; 0) et (yf ; vh × T), voir la figure du haut — notez que les angles sont nécessairement légèrement arrondi en raison des méthodes de fabrication.
Avec une telle came :
- le galet subit un choc à l'entrée de la pente, il se prend un mur incliné ;
- à la fin de la pente, il risque de décoller (effet tremplin) ou bien, si l'effort presseur est suffisant, d'être poinçonné par l'arête vive.
Une telle came n'est donc pas utilisable.
Une première solution consisterait à raccorder les segments de droite par des arcs de cercle dont le rayon est supérieur à celui du galet (figure du milieu). Si le système ne subit plus de choc, en revanche il subit des à-coups important en entrée et en sortie des raccordements circulaires. Par exemple à l'entrée du premier raccord, l'accélération verticale est nulle à gauche ; à droite, le galet est sur une trajectoire circulaire avec une vitesse circonférentielle vh, il subit donc une accélération radiale vh2/R. L'accélération passe donc instantanément de 0 à une valeur non-nulle. Autre manière de voir, c'est comme si le conducteur d'une voiture, pour aborder un virage, tournait brusquement le volant pour passer instantanément d'une trajectoire en ligne droite à un virage de rayon donné.
Cette solution n'est donc possible que pour les faibles vitesses. Ce cas nous permet cependant de relever un point important : la pente au centre (donc la vitesse de montée) est supérieure au cas précédent : lorsque l'on veut limiter l'accélération, cela impose d'augmenter la vitesse maximale.
Pour limiter l'à-coup, il faut que la courbure du profil soit continue ; en effet, la courbure est à peu près égale à la dérivée seconde de la position donc est proportionnelle à l'accélération verticale, une courbure continue implique donc une accélération continue donc un à-coup maîtrisé.
La troisième solution (figure du bas) a un profil en S dont la dérivée seconde est continue. Plusieurs possibilités sont présentées ci-après. Là encore, nous remarquons que pour limiter l'à-coup, nous sommes obligés d'augmenter encore la pente au milieu donc la vitesse maximale.

Considérons maintenant la croix de Malte équipant un projecteur de cinéma analogique. Il s'agit là d'avoir un mouvement de rotation intermittent. L'actionneur est un moteur mettant en mouvement la roue menante munie d'une manivelle (en rouge sur l'image ci-contre) ; l'effecteur, la pièce qui entraîne la pellicule, est reliée à la croix de Malte (en bleu).
La croix de Malte génère un à-coup « infini » en début et en fin de mouvement : il y a un saut d'accélération angulaire. Cependant, la vitesse étant faible (24 images par seconde soit une vitesse moyenne de défilement de 0,576 m/s ≃ 2 km/h et une vitesse de défilement maximale de 1,39 m/s ≃ 5 km/h) et la pellicule étant extrêmement souple, cela ne pose aucun problème si ce n'est le bruit du projecteur qui impose d'isoler phoniquement la cabine de projection de la salle (mais une simple vitre suffit).
La croix de malte est donc un dispositif mécanique conçu pour assurer une fonction — avoir un défilement intermittent alors que l'entraînement du moteur est continu — avec des moyens simples et robustes — pas d'électronique — mais qui impose une loi de mouvement que l'on ne peut pas modifier et qui génère des saccades.
Lois de mouvement couramment utilisées
Pour être sûr d'avoir un à-coup fini (sans pic de Dirac), il faut s'assurer que l'accélération soit continue. Il faut donc avoir une loi en position qui soit dérivable trois fois ; on peut aussi définir la loi à partir d'un profil d'accélération continu (mais pas nécessairement dérivable), puis l'intégrer pour avoir le profil de vitesse puis enfin le profil de déplacement. Dans la conception d'une came, cela revient à s'assurer de la continuité de la courbure : une courbure continue permet d'avoir une accélération radiale continue, sans variation brusque.
Pour l'accélération, on prend en général des lois simples par partie, par exemple :
- linéaire ;
- sinusoïdale ;
- polynomiale.
Le choix de la loi de mouvement est en général un compromis entre avoir une vitesse modérée, pour limiter les frottements et l'énergie dépensée, une accélération modérée, pour limiter les efforts des actionneurs et la puissance nécessaire, et un à-coup modéré, pour éviter les vibrations.
Loi ayant un à-coup infini
Les lois ayant un à-coup théorique infini peuvent être utilisées aux vitesses faibles et pour les systèmes souples, les vibrations générées étant alors modérées. On a recours à de telles lois parce qu'elles sont simples à mettre en œuvre d'un point de vue technologique.
Commutation tout-ou-rien
La manière la plus simple de générer un mouvement consiste à mettre en marche l'actionneur, par un préactionneur (interrupteur, distributeur), puis à le couper lorsque le mouvement arrive en fin de course. La puissance, et donc l'accélération, est en escalier. C'est la loi présentée ci-dessus dans la section Approche élémentaire. Elle est donc trapézoïdale en vitesse et présente des à-coups infinis aux transitions entre les phases.
Si l'on considère une loi en trois phases d'une durée de T/3 — 1/3 du mouvement en accélération, 1/3 du mouvement à vitesse constante et 1/3 du mouvement en freinage —, on a :
- amax = 9/2⋅xf/T2 = 4,5xf/T2 ;
- vmax = 3/2⋅xf/T = 1,5⋅xf/T.
Considérons maintenant un profil de vitesse triangulaire symétrique : on passe d'une phase d'accélération à une phase de freinage sans phase à vitesse constante. On a alors :
- amax = 4⋅xf/T2 ;
- vmax = 2⋅xf/T.
Mouvement harmonique simple


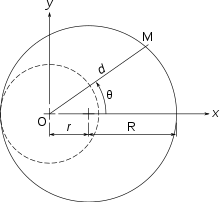
Considérons un excentrique, une came ayant un profil circulaire de rayon R mais dont l'axe de rotation est à une distance r du centre du disque. La distance entre le galet suiveur et l'axe de rotation varie entre deux valeurs x1 = R – r et x2 = R + r.
Si l'on appelle θ l'angle de rotation de la came, l'altitude x est de la forme
- x = R – r⋅cos θ
Si la vitesse de rotation ω est constante, nous avons θ = ωt et donc :
- x = R – r⋅cos ωt ;
- v = +rω⋅sin ωt ;
- a = +rω2⋅cos ωt ;
- j = –rω3⋅sin ωt.
Dans le cas d'un mouvement continu, l'à-coup est limité. Si maintenant on considère une came linéaire dont le profil en S est une sinusoïde de type « altitude = A – B⋅cos(abscisse) » (donc avec une vitesse nulle pour t < 0 et t > T), la situation est similaire à un excentrique qui se met en rotation et s'arrête brusquement (commutation tout-ou-rien) et l'on a donc un à-coup infini au démarrage et à l'arrêt.
La course du système est xf = 2r. Nous avons donc r = xf/2 et ω = π/T soit
- vmax = πxf/2T ≃ 1,57⋅xf/T ;
- amax = π2⋅xf/2T2 ≃ 4,93⋅xf/T2 ;
- jmax = π3⋅xf/2T3 ≃ 15,5⋅xf/T3 (excentrique à fonctionnement continu) ou ∞ (came linéaire).
Cette loi de mouvement est appelée mouvement harmonique simple — MHS ou SHM (anglais : simple harmonic motion).
Loi trapézoïdale en accélération
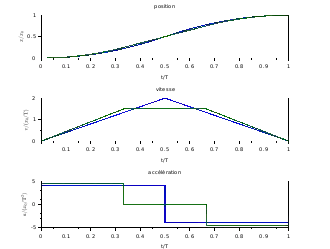
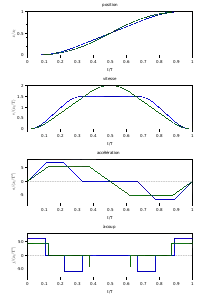 Loi de mouvement trapézoïdale en accélération Lois de mouvement trapézoïdales en accélération :
|
Une loi trapézoïdale en accélération revient à avoir des valeurs discrètes d'à-coup, typiquement {–j0 ; 0 ; +j0}, la grandeur j0 étant constante.
Habituellement, on considère deux phases symétriques (donc d'une durée T/2) : une phase de démarrage (a ≥ 0) et une phase de freinage (a ≤ 0). Pour chaque phase, la sous-phase d'accélération constante (j = 0) occupe la moitié de la phase (donc une durée T/4) et les sous-phases où l'accélération varie (j ≠ 0) occupent un quart de la phase (donc T/8). On obtient les courbes vertes ci-contre.
Nous avons en valeur absolue :
- ;
- ;
- .
Concevons maintenant un mouvement avec une phase de vitesse constante (a = 0), nous avons donc :
- un mouvement globalement en trois parties d'une durée T/3 chacune : a ≥ 0 (démarrage), a = 0 (mouvement uniforme) et a ≤ 0 (freinage) ;
- le démarrage et le freinage sont également en trois parties d'une durée de T/9 chacune, formant une loi trapézoïdale.
Ce sont les courbes bleues ci-contre. Nous avons en valeur absolue :
- ;
- ;
- .
Voir les équations sur la page de description de l'image.
Par rapport à une loi trapézoïdale en vitesse, une loi trapézoïdale en accélération permet de limiter l'à-coup au prix d'une augmentation de l'accélération d'un tiers environ, donc la puissance et l'effort développé sont d'autant plus importants. Par contre, la vitesse maximale reste la même.
Bien sûr, nous ne sommes pas obligé de considérer des fragments tous identiques, les phases d'accélération ou de vitesse constante peuvent être de durées différentes et la loi n'est pas nécessairement symétrique.
Loi trapézoïdale modifiée en accélération

Une loi trapézoïdale modifiée — trap-mod, ou mod-trap (anglais : modified trapezoid) — est une loi trapézoïdale en deux phases dont les sommets des trapèzes sont « arrondis ». Concrètement, les pentes des trapèzes sont remplacées par des lois sinusoïdales.
On a en valeur absolue :
- ;
- ;
- .
Loi sinusoïdale par parties en vitesse et accélération
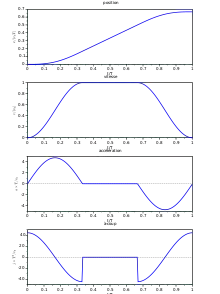
La fonction cosinus possède deux tangentes horizontales sur une période. Ainsi, on peut s'en servir pour faire un raccordement entre deux phases à vitesse constante. On a ainsi une phase d'accélération où la vitesse est de la forme
- ,
une phase de vitesse constante
- v = v0
et une phase de freinage où la vitesse est de la forme
- .
Dans l'exemple ci-contre, nous imposons, comme précédemment, d'avoir trois phases de durées égales T/3. On trouve les valeurs maximales :
- jmax = 27π2xf/(4T3) ≃ 66,6 × xf/T3 ;
- amax = 9πxf/(4T2) ≃ 7,07 × xf/T2 ;
- vmax = v0 = 3xf/(2T) = 1,5 × xf/T.
Voir les équations sur la page de description de l'image.
Nous voyons donc que cette solution est moins favorable que la précédente tant du point de vue de l'accélération (+ 5 %), donc des efforts mis en œuvre, que de l'à-coup (+ 10 %). En revanche, les vitesses maximales sont égales, la dépense énergétique est donc similaire.
Loi cycloïde

La loi cycloïde est sinusoïdale en vitesse et accélération. Dans l'exemple précédent, si nous supprimons la partie centrale où la vitesse est constante, alors les courbes de vitesse et d'accélération sont des sinusoïdes du début à la fin :
soit
La loi x = ƒ(t ) est donc bien une cycloïde (ou plus précisément une trochoïde).
On a alors :
- jmax = 4π2xf/T3 ≃ 39,5 × xf/T3 ;
- amax = 2πxf/T2 ≃ 6,28 × xf/T2 ;
- vmax = v0 = 2 × xf/T.
Loi sinusoïdale modifiée en accélération

Une loi sinusoïdale modifiée — sin-mod, ou mod-sin (anglais : modified sinusoid) — est une loi composée de trois fonctions sinusoïdales :
- la première phase (j ≥ 0) est une fonction sinus entre l'instant initial (t = 0) et T/8 ;
- la deuxième phase (j ≤ 0) est une fonction sinus entre T/8 et 7T/8 ;
- la dernière phase (j ≥ 0) est une fonction sinus entre 7T/8 et T.
Nous avons donc une phase de démarrage en deux parties : un démarrage rapide (0-T/8) suivi d'une accélération « douce » (T/8-T/2), puis une décélération « douce » (T/2-7T/8) suivie d'un freinage rapide (7T/8-T).
Nous avons en valeur absolue :
- ;
- ;
- .
Loi polynomiale
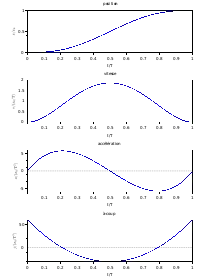
Les conditions initiales et finales imposent six conditions : x(0) = 0, v(0) = 0, a(0) = 0, x(T) = xf, v(T) = 0, a(T) = 0. La fonction x(T) est donc au minimum d'un polynôme de degré cinq :
- x(t ) = c0 + c1t + c2t2 + c3t3 + c4t4 + c5t5.
La solution est unique et vaut :
cette loi est en général appelée « polynôme 3-4-5 ».
Nous avons donc :
et ainsi en valeur absolue :
- jmax = j(0) = j(T) = 60⋅xf/T3 ;
- amax = 10/√3⋅xf/T2 ≃ 5,77⋅xf/T2 ;
- vmax = 15/8⋅xf/T ≃ 1,88⋅xf/T.
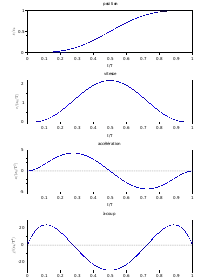
Si l'on impose de plus que l'à-coup soit nul au début et à la fin, on obtient huit conditions et donc un polynôme de degré sept appelé « polynôme 4-5-6-7 ». Nous obtenons :
Nous avons en valeur absolue :
- jmax = j(T/2) = -52.5⋅xf/T3 ;
- amax ≃ 7.513⋅xf/T2 ;
- vmax = 35/16⋅xf/T2 ≃ 2,19⋅xf/T.
Lois de mouvement harmoniques
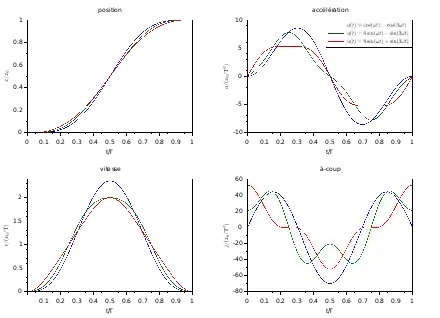
Nous avons vu plus haut la loi de « mouvement harmonique simple ». Le terme « harmonique » fait référence à la décomposition en série de Fourier d'un mouvement périodique ; on un mouvement de période 2T (en considérant qu'un période est un aller-retour pour que le mouvement soit cyclique) et on le décrit par une somme de fonction sinusoïdales de pulsation k⋅ω. La loi cycloïde est un autre exemple de loi harmonique, une harmonique d'ordre 2.
On peut ainsi concevoir un mouvement à deux harmoniques, de type :
- a(t ) = cm⋅cos(mωt ) + cn⋅cos(nωt )
avec ω = π/T. Mais quoi qu'il en soit, si l'on n'effectue qu'une demie période (un aller simple, le mouvement n'est alors pas périodique), l'à-coup n'est fini au début et à la fin que dans certaines circonstances : il faut que l'accélération soit nulle au début et à la fin. Par exemple, si l'on prend
- a(t ) = a0⋅(cos(ωt ) – cos(2ωt ))
on a
- j(0) = 0 puisque a(0) = 0 (car cos(0) = 1)
mais
- j(T) = ∞ puisque a(T) ≠ 0 (car cos(π) = –cos(2π) = –1).
Seules certaines lois harmoniques sont donc adaptées aux vitesses élevées, par exemple
- a(t ) = a0⋅(cos(ωt ) – cos(3ωt )),
- a(t ) = a0⋅(6⋅sin(2ωt ) – sin(6ωt ))
ou bien
- a(t ) = a0⋅(8⋅sin(2⋅ωt) + sin(6⋅ωt)).
Si le comportement mécanique du système piloté peut être modélisé comme un oscillateur harmonique, comme le balancement d'une charge levée par une grue ou un pont roulant ou bien un ensemble rigide que l'on peut modéliser comme un système masse-ressort, alors une loi de mouvement harmonique permet de prédire facilement la réponse du système à la loi de commande.
Concrètement, les lois précédentes donnent :
- Courbe bleue
- a = a0⋅(cos(ωt ) – cos(3ωt ))
-
- vmax ≃ 2,36⋅xf/T
- amax ≃ 8,55⋅xf/T2
- jmax ≃ 69,8⋅xf/T3
- Courbe verte
- a(t ) = a0⋅(6⋅sin(2ωt ) – sin(6ωt ))
-
- vmax ≃ 2⋅xf/T
- amax ≃ 7,76⋅xf/T2
- jmax ≃ 45,0⋅xf/T3
- Courbe rouge
- a(t ) = a0⋅(8⋅sin(2⋅ωt) + sin(6⋅ωt))
-
- vmax ≃ 2⋅xf/T
- amax ≃ 5,29⋅xf/T2
- jmax ≃ 52,1⋅xf/T3
Ces lois sont dites « harmoniques triples » car il y a un facteur trois entre les fréquences (l'harmonique 2 est nulle).
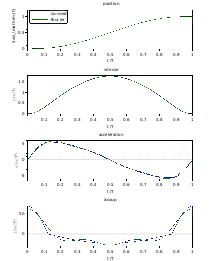
Une telle loi peut être obtenue par développement en série de Fourier ou bien par régression non-linéaire d'une autre loi comme une trap-mod, une sin-mod ou une loi polynomiale. Ainsi, les trois premières harmoniques pour une loi sin-mod donne :
et
Notons que la régression des moindres carrés donne un résultat proche :
Bilan
| Loi | vmax/(xf/T) | amax/(xf/T2) | jmax/(xf/T3) |
|---|---|---|---|
| Triangulaire en vitesse (tout ou rien en accélération) |
2 | 4 | ∞ |
| Trapézoïdale en vitesse 1/3-1/3-1/3 (tout ou rien en accélération) |
1,5 | 4,5 | ∞ |
| Mouvement harmonique simple | 1,57 | 4,93 | 15,5 ou ∞ |
| Trapézoïdale en accélération deux phases1/2-1/2 |
2 | 5,33 | 42,7 |
| Trapézoïdale en accélération trois phases 1/3-1/3-1/3 |
1,5 | 6,75 | 60,8 |
| Trapézoïdale modifiée en accélération (trap-mod) |
4 | 4,89 | 61,4 |
| Sinusoïdale avec vitesse constante 1/3-1/3-1/3 |
1,5 | 7,07 | 66,6 |
| Cycloïde | 2 | 6,28 | 39,5 |
| Sinusoïdale modifiée en accélération (sin-mod) |
1,76 | 5,52 | 69,5 |
| Polynôme 3-4-5 | 1,88 | 5,77 | 60 |
| Polynôme 4-5-6-7 | 2,19 | 7,513 | -52.5 |
Voir aussi
Liens externes
- (en) « Basic cam motion curves », sur Middle East Technical University (Ankara) (consulté le )
- (en) « Motion laws », sur MechDesigner & MotionDesigner Help (consulté le )







































![{\displaystyle x={\frac {x_{\mathrm {f} }}{\mathrm {T} }}\left[t-{\frac {\mathrm {T} }{2\pi }}\sin \left(2\pi {\frac {t}{\mathrm {T} }}\right)\right]}](https://img.franco.wiki/i/75f30b8c295b32d95508e8ea58da3ae9c678db07.svg)
![{\displaystyle v={\frac {x_{\mathrm {f} }}{\mathrm {T} }}\left[1-\cos \left(2\pi {\frac {t}{\mathrm {T} }}\right))\right]}](https://img.franco.wiki/i/13a5d01dd1ddf857754b0e1d20d39852bb8773e8.svg)
















![{\displaystyle x(t)={\frac {1}{16}}x_{\mathrm {f} }\left[8-9\cos \left(\pi {\frac {t}{\mathrm {T} }}\right)+\cos \left(3\pi {\frac {t}{\mathrm {T} }}\right)\right]}](https://img.franco.wiki/i/58b82b938c840b011401000c74567aacbbee014e.svg)
![{\displaystyle x(t)=x_{\mathrm {f} }\left[{\frac {t}{\mathrm {T} }}+{\frac {1}{34\pi }}\left(-18\sin \left(2\pi {\frac {t}{\mathrm {T} }}\right)+{\frac {1}{3}}\sin \left(6\pi {\frac {t}{\mathrm {T} }}\right)\right)\right]}](https://img.franco.wiki/i/3c77423df8361794b4759b0a7b011ce895486d52.svg)
![{\displaystyle x(t)=x_{\mathrm {f} }\left[{\frac {t}{\mathrm {T} }}-{\frac {1}{25\pi }}\left(12\sin \left(2\pi {\frac {t}{\mathrm {T} }}\right)+{\frac {1}{6}}\sin \left(6\pi {\frac {t}{\mathrm {T} }}\right)\right)\right]}](https://img.franco.wiki/i/e0d169894da2a0ce2657921eb33617e6aab11126.svg)
![{\displaystyle a(t)={\frac {x_{\mathrm {f} }}{\mathrm {T} ^{2}}}\left[5,31\sin \left(2\pi {\frac {t}{\mathrm {T} }}\right)+1,38\sin \left(4\pi {\frac {t}{\mathrm {T} }}\right)+0,620\sin \left(6\pi {\frac {t}{\mathrm {T} }}\right)\right]}](https://img.franco.wiki/i/360fac05f3aed5482289c4dcc0bcc070ae8335f5.svg)
![{\displaystyle x(t)=x_{\mathrm {f} }\left[{\frac {t}{\mathrm {T} }}-0,134\cdot \sin \left(2\pi {\frac {t}{\mathrm {T} }}\right)-0,008\,75\cdot \sin \left(4\pi {\frac {t}{\mathrm {T} }}\right)-0,00175\cdot \sin \left(6\pi {\frac {t}{\mathrm {T} }}\right)\right]}](https://img.franco.wiki/i/1579499a7aa89b40a4a08b523c3b3e75ef14c1bd.svg)
![{\displaystyle a(t)={\frac {x_{\mathrm {f} }}{\mathrm {T} ^{2}}}\left[5,34\sin \left(2\pi {\frac {t}{\mathrm {T} }}\right)+1,42\sin \left(4\pi {\frac {t}{\mathrm {T} }}\right)+0,632\sin \left(6\pi {\frac {t}{\mathrm {T} }}\right)\right]}](https://img.franco.wiki/i/2cf2de50b3e80acbda8feab7c10c1b9928423eb5.svg)