Groupe des unités d'un anneau d'entiers quadratiques

Dans tout l'article, ℤ désigne l'anneau des entiers relatifs, ℚ le corps des nombres rationnels, ℝ celui des nombres réels et ℂ celui des complexes. Pour tout anneau d'entiers quadratiques, l'article détaillé montre l'existence d'un élément ω tel que l'anneau est égal à ℤ[ω], c'est-à-dire composé des éléments de la forme a + bω, où a et b sont des entiers relatifs. La valeur ω peut prendre deux formes distinctes : il existe un entier non carré parfait d tel que ω est égal à √d ou, si d est congru à 1 modulo 4, ω soit égal à (1 + √d)/2. L'entier d peut être négatif, la justification du radical √ associé à un nombre strictement négatif se trouve dans l'article détaillé. L'anneau ℤ[ω] est inclus dans le corps ℚ[ω] composé des éléments de la forme a + bω, où a et b sont des rationnels, et dans les deux cas, le corps ℚ[ω] est égal à ℚ[√d].

L'application de conjugaison associe à un élément a + b√d du corps quadratique ℚ[√d] l’élément a – b√d. Dans la suite de l'article, l'élément conjugué d'un élément α du corps est noté α_c. Cette application est un automorphisme de corps et sa restriction à l'anneau ℤ[ω] est aussi un automorphisme (cette fois d'anneau). L'application norme associe à un élément du corps le produit de cet élément avec son conjugué. La norme est à valeurs dans ℚ. Sa restriction à l'anneau ℤ[ω] est à valeurs dans ℤ et s'exprime comme suit :

${\displaystyle \forall a,b\in \mathbb {Z} \quad {\begin{aligned}(1)\quad \omega &={\sqrt {d}}\quad &{\mathcal {N}}(a+b\omega )&=a^{2}-db^{2},\\(2)\quad \omega &={\frac {1}{2}}(1+{\sqrt {d}})\quad &{\mathcal {N}}(a+b\omega )&=a^{2}+ab-{\frac {d-1}{4}}b^{2}.\end{aligned}}}$

Une première propriété permet d'y voir un peu plus clair sur le groupe des unités :

• Un élément de l'anneau ℤ[ω] est inversible si, et seulement si, sa norme est égale à 1 ou à –1[1] ; l'inverse du nombre est alors soit son conjugué, soit l'opposé de son conjugué.

En effet, soit α un élément de ℤ[ω]. S'il est de norme 1 ou –1, alors soit αα_c, soit α(–α_c) est égal à 1. Comme α_c et –α_c sont éléments de l'anneau, α est bien inversible. Réciproquement supposons que β soit l'inverse de α, alors la norme de αβ est égale à 1. La norme de α est un entier qui divise 1. Il n'en existe que deux : 1 et –1, ce qui démontre la proposition.

Remarque. Si d est sans facteur carré et si, dans le cas où d est congru à 1 modulo 4, ω est égal à (1 + √d)/2, alors l'anneau est un peu particulier car il est l'anneau des entiers du corps quadratique. Cette spécificité n'intervient pas ici.

Ce théorème de structure a été démontré par Dirichet pour l'anneau des entiers d'un corps algébrique quelconque[2]. Dans le cas particulier d'un anneau d'entiers quadratiques, deux configurations se présentent.

• Si d est négatif, l'anneau n'est pas inclus dans ℝ et le groupe est fini (par conséquent, c'est un sous-groupe fini du groupe des racines de l'unité, donc un groupe monogène). Plus précisément :Si d est négatif, le groupe des unités est d'ordre quatre si d = –1, six si d = –3 et ω = (1 + i√3)/2, deux sinon.
• Si d est positif, l'anneau est inclus dans ℝ et le groupe est infini[3] :Si d est positif, le groupe des unités est isomorphe au produit direct d'un groupe d'ordre 2 et d'un groupe monogène infini.Dit plus simplement : le groupe des unités (muni de la multiplication) est isomorphe à ℤ/2ℤ × ℤ (muni de l'addition). Tel est le cas par exemple du groupe des unités de l'anneau des entiers de ℚ(√5).

Les éléments du groupe des unités (représenté ici[5] pour d = 5) se trouvent sur quatre branches d'hyperbole obtenues par rotations successives d'un quart de tour.

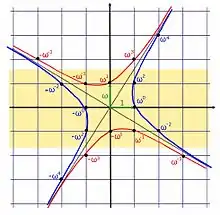
La structure géométrique ne fait véritablement sens que dans le cas où d est positif, celui étudié ici. (1, ω) est une base du ℚ-espace vectoriel ℚ(√d). Toute unité α = x + yω vérifie αα_c = ±1, c'est-à-dire l'une des deux équations :

${\displaystyle x^{2}-dy^{2}=\pm 1\quad {\text{ou}}\quad x^{2}+xy-{\frac {d-1}{4}}y^{2}=\pm 1.}$

Dans les deux cas, en considérant la base (1, ω) comme orthonormale, on observe que chaque unité se trouve sur une des quatre branches de deux hyperboles tournées d'un quart de tour, l'une par rapport à l'autre. Les unités sont les intersections des hyperboles avec les sommets du quadrillage correspondant au réseau ℤ[ω].

À chaque solution α différente de ±1 sont associées trois autres : α_c, –α et –α_c (α_c est égal ou opposé à α⁻¹, selon que N(α) vaut 1 ou –1). Il en existe une par quadrant. Le premier quadrant est formé par les points d'abscisse positive et d'ordonnée strictement positive et les autres sont obtenus par rotation d'un quart de tour (–1 est donc dans le deuxième quadrant et 1 dans le quatrième).

Une solution particulièrement intéressante est celle satisfaisant la définition suivante :

• Une unité fondamentale (en) est une unité ρ telle que toute unité soit égale à ρ^k ou –ρ^k pour un certain entier relatif k.

Il existe quatre unités fondamentales : ρ, ρ_c, –ρ et –ρ_c, selon le théorème de Dirichlet. Celle notée ρ comme dans la preuve ci-dessus est celle du premier quadrant. On peut remarquer que c'est, parmi les unités du premier quadrant (les ρ^k pour k entier > 0), celle de plus petite abscisse.

L'objectif est de trouver l'unité fondamentale ρ présente dans le premier quadrant. Si les deux entiers a et b sont définis par ρ = a + bω, selon la configuration de ω, cela revient à trouver un couple de solution (a, b) d'une des deux équations suivantes avec a et b choisis positifs, (a, b) différent du couple (1,0) et a de valeur la plus petite possible :

${\displaystyle \quad {\begin{aligned}(1)\quad \omega &={\sqrt {d}}\quad &{\mathcal {N}}(a+b\omega )&=a^{2}-db^{2}\\(2)\quad \omega &={\frac {1}{2}}(1+{\sqrt {d}})\quad &{\mathcal {N}}(a+b\omega )&=a^{2}+ab-{\frac {d-1}{4}}b^{2}.\end{aligned}}}$

Plaçons-nous dans le cas (1). Soit h/k une fraction formée de deux entiers strictement positifs tels que h soit différent de 1 et que h² – dk² = ±1. Alors la fraction h/k approche bien ω au sens où la valeur absolue de leur différence est plus petite que l'inverse de 2k². Ceci garantit que h/k est une réduite de la fraction continue de ω. Comme ω est un nombre quadratique, sa fraction continue est périodique à partir d'un certain rang. Les solutions de l'équation x² – dy² = ±1 correspondent aux réduites en avant-dernière position dans la période. Comme les différentes réduites possèdent des numérateurs et dénominateurs strictement croissants, l'unité fondamentale correspond à la réduite de la première période.

Dans le cas où ω est de type (2), les résultats précédents sont toujours valables, mais c'est la fraction continue de –ω_c qui est concernée.

Joseph-Louis Lagrange étudie théoriquement[9] l'équation x² – dy² = ±1. Il montre qu'elle possède une infinité de solutions, que ces solutions se trouvent toutes (au signe près) dans la fraction continue de ω, qu'on en trouve exactement une par période et que sa position correspond à l'avant-dernière. Ces éléments permettent aisément de démontrer le théorème structurel pour les anneaux d'entiers quadratiques, les raisonnements s'appliquant de la même manière pour le type (2).

Supposons que ω soit égal à (1 + √61)/2. On remarque que 61 est un congru à 1 modulo 4. Calculons la fraction continue de –ω_c :

${\displaystyle -\omega _{c}={\frac {1}{2}}({\sqrt {6}}1-1)=3+{\frac {{\sqrt {6}}1-7}{2}}=3+{\cfrac {1}{\frac {{\sqrt {6}}1+7}{6}}},\quad {\frac {{\sqrt {6}}1+7}{6}}=2+{\frac {1}{\frac {{\sqrt {6}}1+5}{6}}}.}$

On continue avec le même algorithme :

${\displaystyle {{\frac {{\sqrt {6}}1+5}{6}}=2+{\frac {1}{\frac {{\sqrt {6}}1+7}{2}}}}\quad {\text{et}}\quad {\frac {{\sqrt {6}}1+7}{2}}=7+{\frac {1}{\frac {{\sqrt {6}}1+7}{6}}}.}$

Le dernier quotient complet est égal au premier, la suite de la fraction est une répétition et l'on possède une période complète. On en déduit la fraction continue, ainsi que l'expression des réduites, notées ici h_i / k_i :

${\displaystyle -\omega _{c}=[3,{\overline {2,{\color {Red}2},7}}]\quad {\text{et}}\quad {\frac {h_{0}}{k_{0}}}=3,\;{\frac {h_{1}}{k_{1}}}={\frac {7}{2}},\;{\frac {h_{2}}{k_{2}}}={\color {Red}{\frac {17}{5}}}}$

L'indice correspondant à l'avant-dernière période est 2, on en déduit que a = 17 et b = 5. On vérifie l'égalité dans l'équation (2). On remarque de (d – 1)/4 est égal à 15 et :

${\displaystyle 17^{2}+17\times 5-15\times 5^{2}=289+85-375=-1\quad {\text{et}}\quad \rho =17+5\omega .}$

La méthode indienne est un peu équivalente à celle des fractions continues. La seule différence dans l'algorithme réside dans le fait que les coefficients de la fraction continue ne sont pas nécessairement positifs. La convention utilisée consiste à choisir le coefficient tel que le quotient complet soit, en valeur absolue le plus grand possible. Elle accélère de fait un peu l'algorithme.

Elle utilise un accélérateur décrit et démontré par Wallis[10] qui s'applique aussi pour les fractions continues. Si l'on dispose un entier quadratique α de norme, en valeur absolue, égale à 2, alors α²/2 est une unité et si l'on dispose d'un entier quadratique de norme, en valeur absolue, égale à 4, alors le huitième de son cube est une unité.

La logique est ici algébrique et non analytique comme chez Lagrange, les démonstrations théoriques associées à l'explicitation de la structure du groupe des unités sont en conséquence plus proches de cet article que des fractions continues. Elles se trouvent dans l'article détaillé. À l'époque de la mise au point de la méthode, les mathématiciens indiens ne se préoccupaient pas de question de cette nature[11]. Les preuves sont la conséquence d'un regard moderne sur leur travail.