Fonction W de Lambert
En mathématiques, et plus précisément en analyse, la fonction W de Lambert, nommée ainsi d'après Jean-Henri Lambert, et parfois aussi appelée la fonction Oméga, est la réciproque de la fonction de variable complexe f définie par f(w) = w ew, c'est-à-dire que pour tous nombres complexes z et w, nous avons :
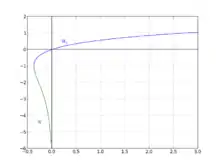
Puisque la fonction f n'est pas injective, W est une fonction multivaluée ou « multiforme » qui comprend deux branches pour les valeurs réelles . Une des branches, la branche principale, W0 peut être prolongée analytiquement en dehors de ]−∞, –1e]. Pour tout nombre complexe z ∉ ]−∞, –1e], on a :
La fonction W de Lambert ne peut pas être exprimée à l'aide de fonctions élémentaires.
Historique
Lambert s'est intéressé à l'équation connue sous le nom d'équation transcendante de Lambert en 1758[1], ce qui conduisit à une note de Leonhard Euler en 1783[2] qui discutait le cas particulier de w ew. La première description de la fonction W semble due à George Pólya et Gábor Szegő en 1925[3]. La fonction de Lambert fut « redécouverte » tous les dix ans environ dans des applications spécialisées, mais son importance ne fut pas vraiment appréciée avant les années 1990. Lorsqu'il fut annoncé que la fonction de Lambert donnait une solution exacte aux valeurs propres de l'énergie du système quantique correspondant au modèle décrit par l'opérateur de Dirac à puits double pour le cas de charges égales — un problème physique fondamental —, Corless et d'autres développeurs du système Maple firent une recherche bibliographique et découvrirent que cette fonction apparait un peu partout dans des applications pratiques[4].
Branches de la « fonction » de Lambert
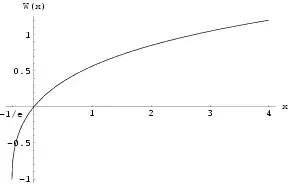

Si nous nous limitons aux arguments réels x ≥ −1e, il existe une fonction et une seule W0 à valeurs réelles telle que
c'est la branche principale de W dans ce domaine. La représentation graphique de W0 figure à droite.
On note généralement W−1 l'autre branche à valeurs réelles, c'est-à-dire la branche correspondant aux arguments x tels que , et à valeurs .
Propriétés élémentaires
Expression de eW(y)
On a W(y) eW(y) = y, donc, si W désigne une des deux branches W0 ou W−1 :
Conséquences de la définition
De l'égalité de la définition, on peut déduire :
- (où W désigne l'une quelconque des deux branches)
- si x ≥ - 1 .
- si x ≤ - 1 .
- (où W désigne l'une quelconque des deux branches et x est non nul)
- si x > 0[5]
Valeurs particulières
Voici quelques valeurs remarquables de W, obtenues simplement en remarquant que f(0)=0, f(1)=e, f(–1)=–1/e, etc. :
- où Ω est la constante oméga
On peut obtenir de même des valeurs complexes de W(x) pour certains x < −1e ; ainsi
Dérivée
Si W désigne une des deux branches W0 ou W−1, la formule de dérivation des bijections réciproques montre que sa dérivée est :
ce qui a pour conséquence que chacune des deux branches de W satisfait l'équation différentielle :
Cette équation est d'ailleurs à variables séparables, et ses solutions sont toutes de la forme (avec k ≠ 0) ou .
Primitives
La fonction W désignant une des deux branches W0 ou W−1, beaucoup de fonctions impliquant W, peuvent être intégrées en utilisant le changement de variable w = W(x), i.e. x = wew :
Méthodes de calcul de W0
Par la série de Taylor
La série de Taylor de W0 au voisinage de 0 peut être obtenue par l'utilisation du théorème d'inversion de Lagrange[6] et est donnée par
Le rayon de convergence est égal à 1e. Cette série peut être prolongée en une fonction holomorphe définie en tout nombre complexe n'appartenant pas à l'intervalle réel ]−∞, –1e] ; cette fonction holomorphe est aussi appelée la branche principale de la fonction W de Lambert.
Nous déduisons de la série de Taylor l'équivalent suivant de W0(x) en 0 :
Comme limite d'une suite
On peut calculer W0(x) de manière itérative, en commençant avec une valeur initiale w0 égale à 1 et en calculant les termes de la suite
- .
Si cette suite converge, on voit aisément que sa limite est W0(x). On démontre que c'est en effet le cas si :
Il est moins simple, mais beaucoup plus efficace, d'utiliser la méthode de Newton, partant de w0 = 1, et posant
cette suite converge (très rapidement) vers W0(x) pour tout x > 1/e.
Développements asymptotiques de W0
On a, pour x tendant vers , le développement asymptotique à trois termes suivant[7] :
On a pour x tendant vers –1/e, le développement asymptotique de W0 :
Développement asymptotique de W−1
On peut également obtenir un développement asymptotique pour W−1 avec x tendant vers 0- :
Paramétrisation des deux branches réelles de la fonction W de Lambert
Les deux branches réelles W0(x) et W–1(x) de la fonction W de Lambert peuvent s'écrire de façon paramétrée.
En effet il existe qui permet d'écrire :[8]
Utilisation
Beaucoup d'équations impliquant des exponentielles peuvent être résolues par l'utilisation de la fonction W. La stratégie générale est de déplacer toutes les instances de l'inconnue d'un côté de l'équation et de le faire ressembler à x ex. À ce point, la « fonction » W nous fournit les solutions :
(chaque branche différente de la « fonction » W donne une solution différente).
Exemples d'applications
Équation 2t = 5t
Par exemple, pour résoudre l'équation 2t = 5t, nous divisons par pour obtenir La définition de la « fonction » W donne alors , soit
Comme cette formule donne deux solutions réelles : et
Équations xx = z et x logb (x) = a
Avec la « fonction » W de Lambert, on peut résoudre des équations du type xx = z (avec et ) par :
donc
et, si , .
Les solutions de l'équation :
(avec et ), équivalente à , sont données avec la « fonction » W de Lambert :
et, si ,
.
La tétration infinie
En général, la tour de puissances infinie converge si et seulement si .
Si r est un nombre réel avec et x le nombre , alors la limite de la suite définie par et est r :
Quand une tétration infinie converge, la fonction W0 de Lambert fournit la valeur de la limite réelle comme :
( si x ≠ 1).
Cela peut être étendu aux nombres complexes z avec la définition :
où Log z représente la branche principale de la fonction logarithme complexe.
Équation x + ex = y
La bijection réciproque de peut être obtenue explicitement : résolvant l'équation on remarque d'abord qu'elle équivaut, en posant à et donc soit :
Équations a ex + bx + c = 0 et a ln(x) + bx + c = 0
Résolution des équations de forme : avec et x dans .
On pose , ce nombre est appelé le discriminant. Il intervient dans la détermination du nombre de solutions de l'équation.
Théorème — Les solutions de l'équation sont:
- Si ou si alors l'équation admet une solution dans .
- Si alors l'équation admet deux solutions dans .
- Si alors n'admet pas de solution dans .
À l'aide du changement de variable x = ln(z), on en déduit la résolution des équations de la forme : avec et x dans . Les solutions sont alors (en n'oubliant pas que W est multivaluée) de la forme :
où .
Équations a λx + bx + c = 0 et a logλ(x) + bx + c = 0
Plus généralement, la fonction W de Lambert permet de résoudre les équations de la forme : et avec et , x dans et .
Il suffit pour cela de considérer une fonction tel que de répéter la démonstration ci-dessus et de considérer la formule de changement de base : . On obtient alors, avec :
et avec :
Il faut alors considérer le nombre pour déterminer la quantité de solutions des équations.
Applications en physique
Constante de Wien
Dans la loi du déplacement de Wien : . La constante de Wien, noté peut être déterminée explicitement à l'aide de la fonction W de Lambert.
Elle vaut : , avec h la constante de Planck, c la vitesse de la lumière dans le vide et kB la constante de Boltzmann.
Courant dans un circuit diode-résistance
La solution pour connaître la valeur du courant dans un circuit en série de diode/résistance peut être donnée par la fonction W de Lambert. Voir la modélisation d'une diode (en).
Diverses formules intégrales
On obtient alors par changements de variable les égalités remarquables :
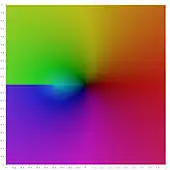
Représentations graphiques
- Représentation de la partie réelle, de la partie imaginaire et du module de la fonction W de Lambert dans le plan complexe



 Les trois fonctions réunies
Les trois fonctions réunies
Généralisations
La fonction W de Lambert fournit des solutions exactes aux équations « algébriques-transcendantes » (en x) de la forme :
ou a0, c et r sont des constantes réelles. La solution est
Les généralisations de la fonction W de Lambert[9] - [10] - [11] incluent :
- un lien entre la relativité générale et la mécanique quantique (gravité quantique) en dimensions réduites[12] où la partie de droite de l'équation (1) est maintenant un polynôme quadratique en x :
- où r1 et r2 sont des constantes réelles, les racines du polynôme quadratique. Dans ce cas, la solution est une fonction avec un seul argument x mais les termes comme ri et a0 sont des paramètres de la fonction. De ce point de vue, la généralisation ressemble à la série hypergéométrique et la fonction de Meijer G mais appartient pourtant à une « classe » différente de fonctions. Quand r1 = r2, chaque côté de (2) peut être factorisé et réduit à (1) et donc la solution se réduit à celle de la fonction standard de W.
L'équation (2) est celle gouvernant le champ d'un dilaton parvenant du modèle R=T- par lequel est dérivée la métrique du système gravitationnel de deux corps dans les dimensions 1+1 (c’est-à-dire une dimension spatiale et une dimension temporelle) pour le cas des masses (au repos) inégales - ainsi que les valeurs propres de l'énergie du système quantique qui est constitué du modèle décrit par l'opérateur de Dirac à puits double pour le cas de charges inégales en une dimension.
- les solutions analytiques pour les valeurs propres de l'énergie d'un cas spécial de la version quantique du problème des trois corps, c’est-à-dire l’ion hydrogène moléculaire (en trois dimensions)[13].
La partie de droite de (1) (ou (2)) est maintenant un quotient de « polynômes » d'ordre infini en x :
- où ri et si sont des constantes réelles distinctes et x est une fonction de la valeur propre de l'énergie et la distance internucléaire R. L'équation (3) avec ces cas spécialisés et exprimés dans (1) et (2) correspond à une classe considérable d'équations à délai différentiel. La « fausse dérivée » de Hardy fournit des racines exactes pour des cas spéciales de (3)[14].
Les applications de la fonction W de Lambert dans les problèmes de la physique fondamentale ne sont pas épuisées même pour le cas standard exprimé dans (1), comme on vient de le voir dans les domaines de la physique atomique et moléculaire, ainsi qu'en optique[15].
Notes
- (la) J. H. Lambert, « Observationes variae in mathesin puram », Acta Helveticae physico-mathematico-anatomico-botanico-medica, vol. III, , p. 128-168 (lire en ligne).
- (la) L. Euler, « De serie Lambertina Plurimisque eius insignibus proprietatibus », Acta Acad. Scient. Petropol., vol. 2, , p. 29-51, réimprimée dans (la) L. Euler, Opera Omnia, Series Prima, vol. 6 : Commentationes Algebraicae, Leipzig, Teubner, (lire en ligne), p. 350-369.
- (en) George Pólya et Gábor Szegő (titre en anglais : Problems and Theorems in Analysis (1998)), Aufgaben und Lehrsätze der Analysis, Berlin, Springer-Verlag, .
- (en) R. M. Corless, G. H. Gonnet, D. E. G. Hare et D. J. Jeffrey, « Lambert's W function in Maple », The Maple Technical Newsletter (MapleTech), vol. 9, , p. 12-22.
- (en) Eric W. Weisstein, « Lambert W-Function », sur MathWorld
- (en) Donatella Merlini, Renzo Sprugnoli et Maria Cecilia Verri, « The method of coefficients », Amer. Math. Monthly, vol. 114, no 1, , p. 40-57.
- On trouvera beaucoup plus de termes de ce développement dans (en) Trott, « Lambert W-Function », sur MathWorld
- (en) « reference request - Parametric representation of the real branches $\operatorname{W_{0}},\operatorname{W_{-1}}$ of the Lambert W function », sur Mathematics Stack Exchange (consulté le )
- (en) T. C. Scott et R. B. Mann, « General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function », AAECC (Applicable Algebra in Engineering, Communication and Computing), vol. 17, no 1, , p. 41-47 (lire en ligne)
- (en) T. C. Scott, G. Fee et J. Grotendorst, « Asymptotic series of Generalized Lambert W Function », SIGSAM (ACM Special Interest Group in Symbolic and Algebraic Manipulation), vol. 47, no 185, , p. 75–83 (lire en ligne)
- T. C. Scott, G. Fee, J. Grotendorst et W.Z. Zhang, « Numerics of the Generalized Lambert W Function », SIGSAM, nos 1/2, , p. 42–56 (lire en ligne)
- (en) P. S. Farrugia, R. B. Mann et T. C. Scott, « N-body Gravity and the Schrödinger Equation », Class. Quantum Grav., vol. 24, , p. 4647-4659 (lire en ligne)
- (en) T. C. Scott, M. Aubert-Frécon et J. Grotendorst, « New Approach for the Electronic Energies of the Hydrogen Molecular Ion », Chem. Phys., vol. 324, , p. 323-338 (lire en ligne)
- (en) Aude Maignan et T. C. Scott, « Fleshing out the Generalized Lambert W Function », SIGSAM, vol. 50, no 2, , p. 45–60 (DOI 10.1145/2992274.2992275)
- (en) T. C. Scott, A. Lüchow, D. Bressanini et J. D. Morgan III, « The Nodal Surfaces of Helium Atom Eigenfunctions », Phys. Rev. A, vol. 75, , p. 060101 (DOI 10.1103/PhysRevA.75.060101)
Références
- (en) R. M. Corless et al., « On the Lambert W function », Adv. Comput. Math., vol. 5, , p. 329-359 (lire en ligne) ou là
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lambert W function » (voir la liste des auteurs).


































![{\displaystyle x\in [-\mathrm {e} ^{-1};\mathrm {e} ]}](https://img.franco.wiki/i/5a856f99799a32d19dc40ebe9e8c57d7104aee06.svg)






![{\displaystyle \alpha \in [0,1]}](https://img.franco.wiki/i/daf3c62599ea71319c85f715c9e590d2bab2d036.svg)
![{\displaystyle \forall x\in \left[-{\frac {1}{\mathrm {e} }},0\right]}](https://img.franco.wiki/i/277e33a7ac52a8ecac9787ef69111ac4bd216b88.svg)














































![{\displaystyle \Delta \in ]-{\frac {1}{\mathrm {e} }};0[}](https://img.franco.wiki/i/33874574c48053058cc6c7bdd562fd24c23f8542.svg)












![{\displaystyle \left]{\frac {-1}{\mathrm {e} }};0\right[}](https://img.franco.wiki/i/af1519e415f659131be5080e281d16fb310c77c0.svg)




























