Courbe parallèle
En géométrie, la parallèle d'une courbe est l'enveloppe d'une famille de cercles congruents centrés sur la courbe. Elle généralise le concept de lignes parallèles (droites). Elle peut également être définie comme une courbe dont les points sont à une distance normale constante d'une courbe donnée[1]. Ces deux définitions ne sont pas entièrement équivalentes car la dernière suppose la régularité, tandis que la première ne le fait pas[2].

Dans la conception assistée par ordinateur, le terme préféré pour une courbe parallèle est courbe décalée[2] - [3] - [4]. (Dans d'autres contextes géométriques, le terme de décalage peut également faire référence à la translation[5]). Les courbes de décalage sont importantes par exemple dans l'usinage à commande numérique, où elles décrivent par exemple la forme de la coupe effectuée par un outil de coupe rond d'une machine à deux axes. La forme de la coupe est décalée de la trajectoire de la fraise d'une distance constante dans la direction normale à la trajectoire de la fraise en chaque point[6].
Dans le domaine de l'infographie 2D connue sous le nom de graphiques vectoriels, le calcul (approximatif) de courbes parallèles est impliqué dans l'une des opérations de dessin fondamentales, appelée trait, qui est généralement appliquée aux polylignes ou polybeziers (eux-mêmes appelés chemins) dans ce domaine[7].
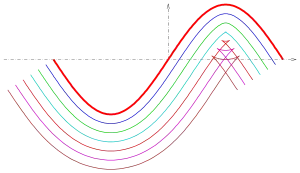
Sauf dans le cas d'une droite ou d'un cercle, les courbes parallèles ont une structure mathématique plus compliquée que la courbe génératrice[1]. Par exemple, même si la courbe de référence est lisse, ses décalages peuvent ne pas l'être ; cette propriété est illustrée dans la figure du haut, en utilisant une courbe sinusoïdale comme courbe génératrice[2]. En général, même si une courbe est algébrique, ses décalages peuvent ne pas l'être. Par exemple, les décalages d'une parabole sont des courbes algébriques, mais les décalages d'une ellipse ou d'une hyperbole ne sont pas algébrique, même si ces courbes génératrices elles-mêmes sont algébriques[3].
La notion se généralise également aux surfaces 3D, où on parle alors de surface décalée ou surface parallèle[8]. L'augmentation d'un volume solide par un décalage de distance (constant) est parfois appelée dilatation[9]. L'opération inverse est parfois appelée bombardement[8]. Les surfaces décalées sont importantes dans l'usinage à commande numérique, où elles décrivent la forme de la coupe effectuée par une fraise hémisphérique d'une machine à trois axes[10]. D'autres formes de coupe peuvent être modélisées mathématiquement par des surfaces décalées générales.
Courbe parallèle d'une courbe paramétrique donnée
S'il existe une représentation paramétrique régulière de la courbe donnée disponible, la deuxième définition d'une courbe parallèle (voir ci-dessus) conduit à la représentation paramétrique suivante de la courbe parallèle avec la distance :
- avec le vecteur normal unitaire .
En coordonnées cartésiennes :
Le paramètre distance peut être négatif. Dans ce cas, on obtient une courbe parallèle sur le côté opposé de la courbe (voir schéma sur les courbes parallèles d'un cercle). On peut facilement vérifier qu'une courbe parallèle à une droite est une droite parallèle au sens commun, et que la courbe parallèle à un cercle est un cercle concentrique.
Propriétés géométriques
- Pour une même valeur paramètre, les vecteurs tangents sont colinéaires :
- En notant la courbure de la courbe donnée, la courbure de la courbe parallèle est donnée par
- et son rayon de courbure par avec le rayon de courbure de la courbe donnée
- Lorsqu'ils existent, les cercles osculateurs de courbes parallèles aux points correspondants sont concentriques[11].
- Comme pour les droites parallèles, une droite normale à une courbe est aussi normale à ses parallèles.
- Lorsque des courbes parallèles sont construites, elles auront des points de rebroussement lorsque la distance de la courbe correspond au rayon de courbure. Ce sont les points où la courbe touche la développée.
- Si la courbe génératrice est une frontière d'un ensemble plan et que sa courbe parallèle est sans auto-intersections, alors cette dernière est la frontière de la somme de Minkowski de l'ensemble plan et du disque de rayon donné[12].
Si la courbe donnée est polynomiale (ce qui signifie que et sont des polynômes), alors les courbes parallèles ne sont généralement pas polynomiales. Dans le domaine de la CAO, c'est un inconvénient, car les systèmes de CAO utilisent des polynômes ou des courbes algébriques. Afin d'obtenir au moins des courbes algébriques, la racine carrée de la représentation de la courbe parallèle doit pouvoir être résolue. Ces courbes sont appelées courbes hodographes pythagoriciennes et ont été étudiées par RT Farouki[13].
Exemples

- Les courbes parallèles à un cercle de centre (x0 , y0) et de rayon r sont les courbes d'équations paramétriques
- Ce sont donc bien des cercles concentriques, de même centre que le cercle de base.
- Les courbes parallèles à une ellipse de centre (x0 , y0) et de demi-axes a et b sont les courbes d'équations paramétriques
- Ce sont des courbes algébriques octiques, dont certaines rappellent la courbe de Talbot.
Courbes parallèles d'une courbe implicite

Généralement la représentation analytique d'une courbe parallèle à une courbe implicite n'est pas possible. Ce n'est que pour les cas simples de lignes et de cercles que les courbes parallèles peuvent être décrites facilement. Par exemple :
- Droite → fonction distance : (forme normale de Hesse)
- Cercle → fonction distance :
En général, en supposant certaines conditions, on peut prouver l'existence d'une fonction de distance orientée . En pratique, il faut le traiter numériquement[14]. En considérant des courbes parallèles, ce qui suit est vrai :
- La courbe parallèle pour la distance d est la ligne de niveau de la fonction de distance orientée correspondante .
Autres exemples

- Les développantes d'une courbe donnée sont un ensemble de courbes parallèles. Par exemple : les développantes d'un cercle sont des spirales parallèles (voir schéma).
Et[16] :
- Une parabole a comme décalages (des deux côtés) des courbes algébriques de degré 6.
- Une hyperbole ou une ellipse a comme décalages (des deux côtés) une courbe algébrique de degré 8.
- Une courbe de Bézier de degré n a pour décalages (à deux côtés) des courbes algébriques de degré 4n − 2 . En particulier, une courbe de Bézier cubique a comme décalages (à deux côtés) des courbes algébriques de degré 10.
Courbe parallèle à une courbe avec un coin
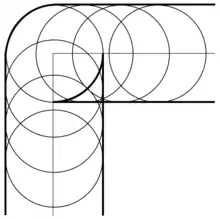
Lors de la détermination du chemin de coupe d'une pièce avec un angle aigu pour l'usinage, il faut définir la courbe parallèle (décalée) à une courbe donnée qui a une normale discontinue au niveau de l'angle. Même si la courbe donnée n'est pas lisse à l'angle aigu, sa courbe parallèle peut être lisse avec une normale continue, ou elle peut avoir des pointes lorsque la distance de la courbe correspond au rayon de courbure à l'angle aigu.
Ventilateurs normaux
Comme décrit ci-dessus, la représentation paramétrique d'une courbe parallèle, , à une courbure donnée, , avec distance est:
- avec le vecteur normal unitaire .
Dans un virage serré (), la normale à donné par est discontinue, c'est-à-dire la limite à gauche de la normale est différente de la limite à droite . Mathématiquement,
- .
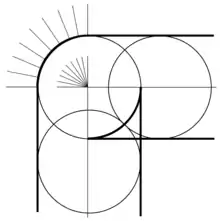
Cependant, on peut définir un ventilateur normal qui fournit une interpolation entre et , et utilise au lieu de à l'angle aigu :
- où .
La définition résultante de la courbe parallèle fournit le comportement souhaité :
Algorithmes
En général, la courbe parallèle d'une courbe de Bézier n'est pas une autre courbe de Bézier, un résultat prouvé par Tiller et Hanson en 1984[17]. Ainsi, en pratique, des techniques d'approximation sont utilisées. Tout niveau de précision souhaité est possible en subdivisant à plusieurs reprises la courbe, bien que de meilleures techniques nécessitent moins de subdivisions pour atteindre le même niveau de précision. Une étude réalisée en 1997 par Elber, Lee et Kim[18] est largement citée, bien que de meilleures techniques aient été proposées plus récemment. Une technique moderne basée sur l'ajustement de courbe, avec des références et des comparaisons avec d'autres algorithmes, ainsi qu'un code source JavaScript open source, a été publiée dans un article de blog[19] en septembre 2022.
Un autre algorithme efficace pour la compensation est l'approche par niveau décrite par Kimmel et Bruckstein (1993)[20].
Surfaces parallèles (décalées)

Les surfaces décalées sont importantes dans l'usinage à commande numérique, où elles décrivent la forme de la coupe effectuée par une fraise à bout sphérique d'une fraise à trois axes[10]. S'il existe une représentation paramétrique régulière de la surface donnée disponible, la deuxième définition d'une courbe parallèle (voir ci-dessus) se généralise à la représentation paramétrique suivante de la surface parallèle avec la distance :
- avec le vecteur normal .
Le paramètre de distance peut aussi être négatif. Dans ce cas, on obtient une surface parallèle sur le côté opposé de la surface (voir schéma similaire sur les courbes parallèles d'un cercle). On vérifie facilement qu'une surface parallèle à un plan est un plan parallèle au sens commun et la surface parallèle d'une sphère est une sphère concentrique.
Propriétés géométriques
- Pour un même paramètre, les vecteurs tangents sont colinéaires[21]:
- Les vecteurs normaux pour un même paramètre ont même direction :
- où et sont les opérateurs de forme pour et , respectivement.
- Les courbures principales sont les valeurs propres de l'opérateur de forme, les directions de courbure principales sont ses vecteurs propres, la courbure gaussienne est son déterminant et la courbure moyenne est la moitié de sa trace.
- où et sont les inverses des opérateurs de forme pour et , respectivement.
- Les rayons de courbure principaux sont les valeurs propres de l'inverse de l'opérateur de forme, les directions de courbure principales sont ses vecteurs propres, l'inverse de la courbure gaussienne est son déterminant et le rayon de courbure moyen est la moitié de sa trace.
On remarque ainsi une similarité avec les propriétés géométriques des courbes parallèles.
Généralisations
Le problème se généralise assez évidemment aux dimensions supérieures, par exemple aux surfaces décalées, et un peu moins trivialement aux surfaces de tuyaux[22]. Il est à noter que la terminologie pour les versions de dimension supérieure varie encore plus largement que dans le cas planaire, par exemple d'autres auteurs parlent de fibres parallèles, de rubans et de tubes[23]. Pour les courbes intégrées dans des surfaces 3D, le décalage peut être pris le long d'une géodésique[24].
Une autre façon de généraliser est (même en 2D) de considérer une distance variable, par exemple paramétrée par une autre courbe[21]. On peut par exemple tracer (enveloppe) avec une ellipse au lieu d'un cercle[21] comme c'est possible par exemple dans Metafont.
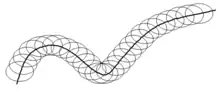
Plus récemment, Adobe Illustrator a ajouté une fonctionnalité quelque peu similaire dans la version CS5, bien que les points de contrôle pour la largeur variable soient spécifiés visuellement[25]. Dans les contextes où il est important de faire la distinction entre compensation de distance constante et variable, les acronymes CDO et VDO sont parfois utilisés[9].
Courbes de décalage générales
Soient une représentation paramétrique régulière d'une courbe, , et une seconde courbe paramétrable par sa normale unitaire, , où la normale de (cette paramétrisation par la normale existe pour les courbes dont la courbure est strictement positive ou négative, et donc convexe, lisse, et non droite). La représentation paramétrique de la courbe générale de décalage de compensé par est:
- où est la normale unitaire de .
On voit bien que le décalage trivial, , donne des courbes parallèles ordinaires (c'est-à-dire décalées).
Propriétés géométriques
- Pour un paramètre donné, les vecteurs tangents sont colinéaires[21]:
- Comme pour les lignes parallèles, une normale à une courbe est également normale à ses décalages généraux.
- avec la courbure de la courbe générale de décalage, la courbure de , et la courbure de pour le paramètre .
- avec le rayon de courbure de la courbe générale de décalage, le rayon de courbure de , et le rayon de courbure de pour le paramètre .
- Lorsque des courbes de décalage générales sont construites, elles auront des pointes lorsque la courbure de la courbe correspond à la courbure du décalage. Ce sont les points où la courbe touche la développée.
Surfaces décalées générales
Les surfaces décalées générales décrivent la forme des coupes effectuées par une variété de mèches de coupe utilisées par les fraises en bout à trois axes dans l'usinage à commande numérique . On suppose qu'on a une représentation paramétrique régulière d'une surface, , et une deuxième surface qui peut être paramétrée par sa normale unitaire, , où la normale de (cette paramétrisation par normale existe pour les surfaces dont la courbure gaussienne est strictement positive, et donc convexe, lisse, et non plate). La représentation paramétrique de la surface décalée générale de compensé par est:
- où est la normale unitaire de .
Une fois encore, le décalage trivial, , donne des surfaces parallèles ordinaires (c'est-à-dire décalées).
Propriétés géométriques
- Comme pour les droites parallèles, le plan tangent d'une surface est parallèle au plan tangent de ses décalages généraux[21].
- Comme pour les lignes parallèles, une normale à une surface est également normale à ses décalages généraux[21].
- où et sont les opérateurs de forme pour et , respectivement.
- Les courbures principales sont les valeurs propres de l' opérateur de forme, les directions de courbure principales sont ses vecteurs propres, la courbure gaussienne est son déterminant et la courbure moyenne est la moitié de sa trace .
- où et sont les inverses des opérateurs de forme pour et , respectivement.
- Les rayons de courbure principaux sont les valeurs propres de l'inverse de l' opérateur de forme, les directions de courbure principales sont ses vecteurs propres, l'inverse de la courbure gaussienne est son déterminant et le rayon de courbure moyen est la moitié de sa trace .
Là encore, il y a similarité avec les propriétés géométriques des courbes de décalage générales.
Dérivation des propriétés géométriques pour les décalages généraux
Les propriétés géométriques répertoriées ci-dessus pour les courbes et les surfaces décalées générales peuvent être dérivées pour des décalages de dimension arbitraire. Soit une représentation paramétrique régulière d'une surface à n dimensions, , où la dimension de est n-1. Supposons également que vous ayez une deuxième surface à n dimensions qui peut être paramétrée par sa normale unitaire, , où la normale de (cette paramétrisation par normale existe pour les surfaces dont la courbure gaussienne est strictement positive, et donc convexe, lisse, et non plate). La représentation paramétrique de la surface décalée générale de compensé par est:
- où est la normale unitaire de . (Le décalage trivial, , donne des surfaces parallèles ordinaires. )
On remarque tout d'abord que la normale de la normale de par définition. Maintenant, nous allons appliquer le différentiel par rapport à en , qui donne ses vecteurs tangents générant son plan tangent.
Il apparait que les vecteurs tangents pour sont la somme des vecteurs tangents pour et son décalage , qui partagent la même unité normale. Ainsi, la surface décalée générale partage le même plan tangent et normal avec et . Cela correspond à la nature des enveloppes.
On considère maintenant les équations de Weingarten pour l' opérateur de forme, qui peut être écrit comme . Si est inversible, . Il faut rappeler que les courbures principales d'une surface sont les valeurs propres de l'opérateur de forme, les directions de courbure principales sont ses vecteurs propres, la courbure de Gauss est son déterminant et la courbure moyenne est la moitié de sa trace. L'inverse de l'opérateur de forme conserve ces mêmes valeurs pour les rayons de courbure.
En remplaçant dans l'équation la différentielle de , on a:
- où est l'opérateur de forme pour .
Ensuite, on utilise à nouveau les équations de Weingarten pour remplacer :
- où est l'opérateur de forme pour .
Ensuite, on résout pour et multiplie des deux côtés par pour revenir aux équations de Weingarten, cette fois pour :
Ainsi, , et l'inversion des deux côtés donne .
Voir également
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Parallel curve » (voir la liste des auteurs).
- Frederick Newton Willson, Theoretical and Practical Graphics, Macmillan, (ISBN 978-1-113-74312-1, lire en ligne), 66
- Satyan L. Devadoss et Joseph O'Rourke, Discrete and Computational Geometry, Princeton University Press, , 128–129 p. (ISBN 978-1-4008-3898-1, lire en ligne)
- J. Rafael Sendra, Franz Winkler et Sonia Pérez Díaz, Rational Algebraic Curves: A Computer Algebra Approach, Springer Science & Business Media, (ISBN 978-3-540-73724-7, lire en ligne), p. 10
- Max K. Agoston, Computer Graphics and Geometric Modelling: Mathematics, Springer Science & Business Media, (ISBN 978-1-85233-817-6, lire en ligne), p. 586
- John Vince, Geometry for Computer Graphics: Formulae, Examples and Proofs, Springer Science & Business Media, (ISBN 978-1-84628-116-7, lire en ligne), p. 293
- Duncan Marsh, Applied Geometry for Computer Graphics and CAD, 2nd, (ISBN 978-1-84628-109-9, lire en ligne), p. 107
- http://www.slideshare.net/Mark_Kilgard/22pathrender, p. 28
- Max K. Agoston, Computer Graphics and Geometric Modelling, Springer Science & Business Media, , 638–645 p. (ISBN 978-1-85233-818-3, lire en ligne)
- http://www.cc.gatech.edu/~jarek/papers/localVolume.pdf, p. 3
- I. D. Faux et Michael J. Pratt, Computational Geometry for Design and Manufacture, Halsted Press, (ISBN 978-0-47026-473-7, OCLC 4859052)
- Fiona O'Neill: Planar Bertrand Curves (with Pictures!).
- E. Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. S. 30.
- Rida T. Farouki: Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable (Geometry and Computing). Springer, 2008, (ISBN 978-3-540-73397-3).
- E. Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. S. 81, S. 30, 41, 44.
- J.A. Thorpe: Elementary topics in Differential Geometry, Springer-Verlag, 1979, (ISBN 0-387-90357-7).
- http://faculty.engineering.ucdavis.edu/farouki/wp-content/uploads/sites/41/2013/02/Introduction-to-PH-curves.pdf, p. 16 "taxonomy of offset curves"
- Tiller et Hanson, « Offsets of Two-Dimensional Profiles », IEEE Computer Graphics and Applications, vol. 4, no 9, , p. 36-46 (DOI 10.1109/mcg.1984.275995)
- Elber, Lee et Kim, « Comparing offset curve approximation methods », IEEE Computer Graphics and Applications, vol. 17, no 3, may–jun 1997, p. 62-71 (DOI 10.1109/38.586019, lire en ligne)
- Levien, « Parallel curves of cubic Béziers », (consulté le )
- Kimmel and Bruckstein (1993) Shape offsets via level sets CAD (Computer Aided Design) 25(3):154–162.
- Eric L. Brechner, Geometry Processing for Design and Manufacturing, SIAM, , 101– (ISBN 978-0-89871-280-3), « 5. General Offset Curves and Surfaces »
- Helmut Pottmann et Johannes Wallner, Computational Line Geometry, Springer Science & Business Media, , 303–304 p. (ISBN 978-3-540-42058-3, lire en ligne)
- Gregory S. Chirikjian, Stochastic Models, Information Theory, and Lie Groups, Volume 1: Classical Results and Geometric Methods, Springer Science & Business Media, , 171–175 p. (ISBN 978-0-8176-4803-9)
- Advances in geometric modeling, Wiley, (ISBN 978-0-470-85937-7, lire en ligne), p. 72
- http://design.tutsplus.com/tutorials/illustrator-cs5-variable-width-stroke-tool-perfect-for-making-tribal-designs--vector-4346 application of the generalized version in Adobe Illustrator CS5 (also video)
- Josef Hoschek: Offset curves in the plane. In: CAD. 17 (1985), S. 77–81.
- Takashi Maekawa: An overview of offset curves and surfaces. In: CAD. 31 (1999), S. 165–173.
Liens externes
- (en) Eric W. Weisstein, « ParallelCurves », sur MathWorld
- Courbes parallèles sur mathcurve.com
- (en) R. T. Farouki et C. A. Neff, « Analytic properties of plane offset curves », Computer Aided Geometric Design, vol. 7, nos 1–4, , p. 83–99 (DOI 10.1016/0167-8396(90)90023-K)
- (en) Les A. Piegl, « Computing offsets of NURBS curves and surfaces », Computer-Aided Design, vol. 31, no 2, , p. 147–156 (DOI 10.1016/S0010-4485(98)00066-9, CiteSeerx 10.1.1.360.2793)
- (en) Ian R. Porteous, Geometric Differentiation: For the Intelligence of Curves and Surfaces, Cambridge University Press, , 2nd éd., 1–25 p. (ISBN 978-0-521-00264-6)
- (en) Nicholas M. Patrikalakis et Takashi Maekawa, Shape Interrogation for Computer Aided Design and Manufacturing, Springer Science & Business Media, (1re éd. 2002) (ISBN 978-3-642-04074-0), Chapter 11. Offset Curves and Surfaces Free online version.
- (en) François Anton, Ioannis Z. Emiris, Bernard Mourrain et Monique Teillaud « Modèle {{Lien conférence}} : titre communication manquant »
—International Conference on Computational Science and its Applications (Singapore, ) - (en) Rida T. Farouki, Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable, Springer Science & Business Media, , 141–178 p. (ISBN 978-3-540-73397-3) Pages listed are the general and introductory material.
- (en) Y.-S. Ma (éd.) et Y.-S. Ma, Semantic Modeling and Interoperability in Product and Process Engineering: A Technology for Engineering Informatics, Springer Science & Business Media, , 259–273 p. (ISBN 978-1-4471-5073-2), « Computation of Offset Curves Using a Distance Function: Addressing a Key Challenge in Cutting Tool Path Generation »



































































































