Composé polyédrique

Un composé polyédrique est un polyèdre qui est lui-même composé de plusieurs autres polyèdres partageant un centre commun, l'analogue tridimensionnel des composés polygonaux (en) tels que l'hexagramme.

Les sommets voisins d'un composé peuvent être connectés pour former un polyèdre convexe appelé l'enveloppe convexe. Le composé est un facettage de l'enveloppe convexe.

Un autre polyèdre convexe est formé par le petit espace central commun à tous les membres du composé. Ce polyèdre peut être considéré comme le noyau pour un ensemble de stellations incluant ce composé. (Voir la liste des modèles de polyèdres de Wenninger (en) pour ces composés et plus de stellations.)

Le dual d'un composé de polyèdres est le composé des duaux de ces polyèdres.

Composés réguliers

Un composé polyédrique régulier peut être défini comme un composé qui, comme un polyèdre régulier, est isogonal, isotoxal, et isoédrique. Avec cette définition, il existe 5 composés réguliers.

Composé	Enveloppe convexe	Noyau	Symétrie	Composé dual-régulier
Composé de deux tétraèdres, ou octangle étoilé	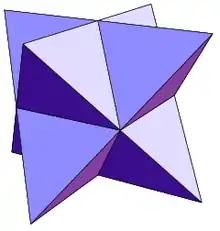Cube	Octaèdre	O_h	Composé de deux tétraèdres
Composé de cinq tétraèdres (en)	Dodécaèdre	Icosaèdre	I	Composé jumeau chiral de cinq tétraèdres
Composé de dix tétraèdres (en)	Dodécaèdre	Icosaèdre	I_h	Composé de dix tétraèdres
Composé de cinq cubes (en)	Dodécaèdre	Triacontaèdre rhombique	I_h	Composé de cinq octaèdres
Composé de cinq octaèdres (en)	Icosidodécaèdre	Icosaèdre	I_h	Composé de cinq cubes

Le plus connu est le composé de deux tétraèdres, souvent appelé l'octangle étoilé, un nom donné par Kepler. Les sommets des deux tétraèdres définissent un cube, et l'intersection des deux : un octaèdre, qui partage les mêmes plans de faces que le composé. Ainsi, c'est une stellation de l'octaèdre.

L'octangle étoilé peut aussi être regardé comme un composé dual-régulier.

Le composé de cinq tétraèdres (en) se décline en 2 versions énantiomorphes, qui ensemble forment le composé de 10 tétraèdres. Chaque composé tétraédrique est autodual ou dual de son jumeau chiral, et le composé de 5 cubes est le dual du composé de 5 octaèdres.

Remarque : il y a 2 positions pour placer les sommets du tétraèdre régulier sur des sommets du cube, 5 positions pour placer les sommets du cube sur des sommets du dodécaèdre régulier, 10 positions pour placer les sommets du tétraèdre régulier sur des sommets du dodécaèdre régulier, et 5 positions pour placer les sommets de l'icosaèdre régulier sur les arêtes de l'octaèdre régulier.

Composé dual-régulier

Un composé dual-régulier est composé d'un polyèdre régulier (un des solides de Platon ou des solides de Kepler-Poinsot) et de son dual régulier, arrangés réciproquement sur une sphère intermédiaire commune, telle que l'arête d'un polyèdre coupe l'arête duale du polyèdre dual. Il existe cinq composés duaux-réguliers.

Composé dual-régulier	Enveloppe convexe	Noyau	Symétrie
Composé de deux tétraèdres	Cube	Octaèdre	O_h
Composé du cube et de l'octaèdre	Dodécaèdre rhombique	Cuboctaèdre	O_h
Composé de l'icosaèdre et du dodécaèdre	Triacontaèdre rhombique	Icosidodécaèdre	I_h
Composé du grand icosaèdre et du grand dodécaèdre étoilé	Dodécaèdre	Icosaèdre	I_h
Composé du petit dodécaèdre étoilé et du grand dodécaèdre	Icosaèdre	Dodécaèdre	I_h

Le composé dual-régulier d'un tétraèdre avec son polyèdre dual est aussi l'octangle étoilé régulier, puisque le tétraèdre est autodual.

Les composés duaux-réguliers cube-octaèdre et dodécaèdre-icosaèdre sont les premières stellations du cuboctaèdre et de l'icosidodécaèdre, respectivement.

Le composé du petit dodécaèdre étoilé et du grand dodécaèdre ressemble extérieurement au petit dodécaèdre étoilé, parce que le grand dodécaèdre est complètement contenu à l'intérieur.

Composés uniformes

En 1976, John Skilling publia Uniform Compounds of Uniform Polyhedra (Composés uniformes de polyèdres uniformes) qui énumère 75 composés (incluant 6 ensembles prismatiques infinis de composés, #20-#25) fait à partir de polyèdres uniformes avec une symétrie rotationnelle. (Chaque sommet est de sommet uniforme et chaque sommet est transitif avec chaque autre sommet). Cette liste inclut les cinq composés réguliers ci-dessus[1].

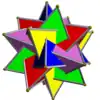
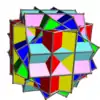
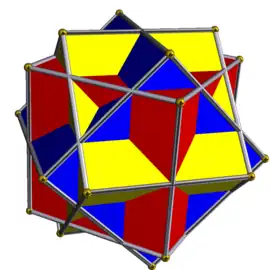
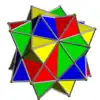
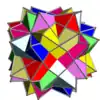
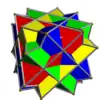
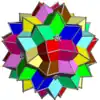
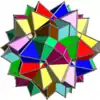
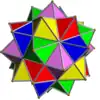
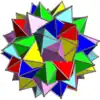
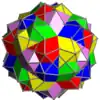
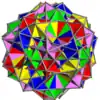
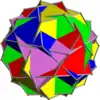
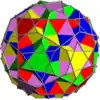
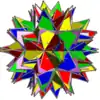
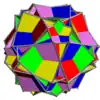
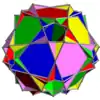
Voici une table imagée des 75 composés uniformes listée par Skilling. La plupart sont colorés par chaque élément polyédrique. Certains, comme les paires chirales, sont colorés par symétrie des faces avec chaque polyèdre.

1-19 : Divers (4,5,6,9 et 17 sont les 5 composés réguliers)

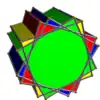
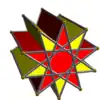
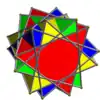
20-25 : Symétrie prismatique incluse dans la symétrie diédrique,

26-45 : Symétrie prismatique incluse dans la symétrie octédrique ou icosaédrique,

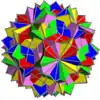
46-67 : Symétrie tétraédrique incluse dans la symétrie octaédrique ou icosaédrique,

68-75 : paires énantiomorphes

Notes et références

Note

(en) The 75 Uniform Compounds of Uniform Polyhedra

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Polyhedral compound » (voir la liste des auteurs).
(en) John Skilling, « Uniform Compounds of Uniform Polyhedra », dans Mathematical Proceedings of the Cambridge Philosophical Society, vol. 79, 1976, p. 447-457
(en) Peter R. Cromwell, Polyhedra, Cambridge, 1997
(en) Magnus Wenninger (en), Dual Models, Cambridge, CUP, 1983, p. 51-53
(en) Michael G. Harman, Polyhedral Compounds, unpublished manuscript, circa 1974
(de) Edmund Hess (en), « Zugleich Gleicheckigen und Gleichflächigen Polyeder », dans Schriften der Gesellschaft zur Berörderung der gesammten Naturwissenschaften zu Marburg, vol. 11, 1876, p. 5-97
(la) Luca Pacioli, De divina proportione, 1509

Liens externes

(en) Eric W. Weisstein, « Polyhedron Compound », sur MathWorld
(en) Stella: Polyhedron Navigator – Logiciel qui peut imprimer des réseaux de beaucoup de composés.
(en) Compounds of Polyhedra – de Virtual Reality Polyhedra
(en) Uniform Compounds of Uniform Polyhedra
(en) Polyhedral Compounds
(en) Modular Origami VRML Models

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.