Calcul fonctionnel holomorphe
En mathématiques, et plus précisément en analyse, le calcul fonctionnel holomorphe désigne l'application du calcul fonctionnel aux fonctions holomorphes, c'est-à-dire qu'étant donnés une fonction holomorphe ƒ de la variable complexe z et un opérateur linéaire T, l'objectif est de construire un opérateur f (T) étendant ƒ de manière « naturelle ».
Le cas le plus fréquent est celui où T est un opérateur borné sur un espace de Banach. En particulier, en dimension finie, T peut être identifié à une matrice carrée à coefficients complexes ; ce cas permet d'illustrer les idées du calcul fonctionnel, et sert souvent de motivation heuristique aux techniques d'analyse d'opérateurs plus généraux
Motivations
Nécessité d'un calcul fonctionnel général
On suppose dans cette section que T est une matrice carrée n × n à coefficients complexes.
Pour certaines fonctions simples f, il y a des façons naturelles de définir f (T). Par exemple, si est un polynôme à coefficients complexes, il suffit de remplacer z par T pour définir , où T0 = I, la matrice identité (d'ordre n). C'est le calcul fonctionnel polynomial, définissant un homomorphisme de l'algèbre des polynômes vers l'algèbre des matrices n × n.
Ce cas se généralise sans difficulté à celui d'une fonction partout holomorphe, c'est-à-dire à une fonction entière, pour laquelle la série de Taylor a un rayon de convergence infini. Dans ce cas, en effet, définissant , cette série convergera (plus généralement, elle convergera normalement si T est un opérateur borné pour la norme utilisée).
Un exemple important est le cas de l'application exponentielle, et en particulier de l'exponentielle de matrice. On obtient (prenant pour f la fonction exponentielle usuelle)
Il n'est pas vraiment nécessaire que la série de Taylor de f converge partout ; il est clair qu'il suffit que son rayon de convergence soit supérieur à , la norme d'opérateur de T. Bien que cela permet d'étendre la classe des fonctions f pour lesquelles on peut définir f (T), cela est loin d'être suffisant dans tous les cas. Ainsi, on sait (voir logarithme d'une matrice) que toute matrice T non singulière possède un logarithme, c'est-à-dire une matrice S telle que eS = T. Ce logarithme ne peut pas être construit en général à l'aide d'une série entière, car la série est de rayon de convergence 1, et donc la série correspondante ne donnera pas ln(T + I), même si T + I est inversible, dès que C'est ce qui explique la nécessité d'un calcul fonctionnel plus général.
Le calcul fonctionnel et le spectre
On s'attend à ce qu'une condition nécessaire pour que f (T) ait un sens est que f soit définie sur le spectre de T. Ainsi, pour toute matrice diagonalisable T (c'est-à-dire telle que T = PDP−1, où D est une matrice diagonale), on a une définition naturelle de f (T) donnée par f (T) = P f (D) P−1, où f (D) est la matrice diagonale dont les éléments sont les images par f de ceux de D. Cette construction échoue si f n'est pas définie sur certains de ces éléments diagonaux, lesquels sont les valeurs propres de T.
D'autres indications tendent à confirmer cette idée. Ainsi, si , une définition raisonnable de f (T) serait f (T) = (T – 2I)−1(T – 5I)−1. Cependant, cette expression n'a pas de sens si les inverses du membre de droite n'existent pas, et donc si 2 ou 5 sont des valeurs propres de T.
Plus généralement, pour un opérateur borné T, f devra être définie sur les valeurs spectrales de T, c'est-à-dire sur les nombres complexes λ pour lesquels l'opérateur T – λI n'a pas un inverse qui soit un opérateur continu ; toute valeur propre est une valeur spectrale, mais la réciproque n'est pas vraie en général.
Le calcul fonctionnel holomorphe pour un opérateur borné
Soit X un espace de Banach complexe, et L(X) la famille des opérateurs bornés sur X ; si est holomorphe sur un ouvert simplement connexe D du plan complexe, et si Γ est une courbe de Jordan rectifiable dans D (c'est-à-dire une courbe fermée ne se recoupant pas), la formule intégrale de Cauchy dit que
pour tout z à l’intérieur de Γ (c'est-à-dire tel que l'indice de z par rapport à Γ soit égal à 1).
L'idée du calcul fonctionnel holomorphe est d'étendre cette formule à des fonctions prenant leurs valeurs dans l'espace L(X). On aurait donc la définition (purement formelle à ce stade) :
où (ζ – T)-1 est la résolvante de T en ζ.
Admettant que cette intégrale ait été définie, ce calcul fonctionnel implique les conditions nécessaires suivantes :
- La formule de Cauchy s'appliquant à des fonctions holomorphes f, une notion convenable d'holomorphie doit être définie pour des fonctions prenant leurs valeurs dans l'espace de Banach L(X).
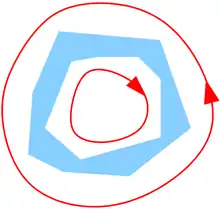
- L'application résolvante ζ ↦ (ζ - T)-1 n'étant pas définie sur le spectre de T, σ(T), la courbe de Jordan Γ ne doit pas rencontrer σ(T). L'application résolvante étant holomorphe sur le complémentaire de σ(T), Γ doit encercler au moins une partie de σ(T), pour obtenir un calcul fonctionnel non trivial
- Il devrait y avoir unicité du calcul fonctionnel, et donc f(T) doit être indépendant de Γ.
Une définition précise du calcul fonctionnel holomorphe satisfaisant ces exigences, pour T ∈ L(X), est, comme précédemment, où f est une fonction holomorphe sur un ouvert D contenant σ(T), et est une collection de courbes de Jordan dans D telle que σ(T) soit à l'intérieur de Γ, et que chaque γi soit orienté dans le sens positif. L'ensemble D dépend de f, et n'est pas nécessairement simplement connexe, ni même connexe, comme illustré ci-contre.
Les sous-sections suivantes précisent le sens de cette définition, en particulier celui de l'intégrale, et démontrent l'unicité de f(T).
Intégration à valeurs dans un espace de Banach
Pour une fonction continue g définie sur un voisinage ouvert de Γ et prenant ses valeurs dans L(X), l'intégrale de contour ∫Γg est définie de façon analogue au cas scalaire : on paramètre chaque γi ∈ Γ par un intervalle réel [a, b], et l'intégrale est la limite des sommes de Riemann obtenues pour des partitions de plus en plus fines de [a, b], ces sommes convergeant au sens de la norme des opérateurs (g étant continue, il n'est pas nécessaire d'utiliser une intégrale plus générale, telle que l'intégrale de Bochner). On définit alors
ƒ est supposée être holomorphe (donc continue) sur un voisinage ouvert de Γ ; il en est de même de l'application résolvante, comme ce sera démontré plus bas ; ainsi, l'intégrale est bien définie.
L'application résolvante
L'application s'appelle l’application résolvante de T. Elle est définie sur le complémentaire du spectre σ(T), appelé l’ensemble résolvant de T, et que l'on notera désormais ρ(T). La théorie classique des fonctions holomorphes complexes repose sur les propriétés de l'intégrale ; le calcul fonctionnel holomorphe fait jouer un rôle analogue aux propriétés de l'intégrale de la résolvante ; celles-ci sont détaillées ci-dessous.
Une formule pour la résolvante
Un calcul direct montre que, pour z1, z2 ∈ ρ(T), On en déduit que
Cette équation est appelée la première formule de la résolvante. Elle montre que (z1 − T)−1 et (z2 − T)−1 commutent ; on s'attend donc à ce que les opérateurs construits par le calcul fonctionnel holomorphe commutent également. Faisant tendre z2 vers z1, on voit que l'application résolvante est différentiable dans les complexes en tout z1 ∈ ρ(T) ; l'intégrale donnée précédemment est donc définie pour tous les opérateurs de L(X).
Holomorphie
En fait, l'ensemble résolvant ρ(T) est un ouvert, et l'application résolvante y est non seulement différentiable, mais holomorphe, ou plus exactement analytique, c'est-à-dire développable en série entière ; cette propriété sera fréquemment utilisée par la suite. Pour la démontrer, on prend z1 ∈ ρ(T) et on remarque que, formellement, , ce qui amène à considérer la série
qui doit valoir (z2 − T)−1 si elle converge. Comme cette série converge dans L(X) si , on en déduit le résultat annoncé : l'application résolvante est développable en série entière dans un disque ouvert centré en z1.
Série de Neumann
Une autre expression de (z − T)−1 est également utile. On obtient comme dans la section précédente la série appelée série de Neumann, qui converge vers (z − T)−1 si
Compacité du spectre
Les deux résultats précédents montrent que, pour un opérateur borné T, le spectre σ(T) est un fermé (puisque complémentaire d'un ouvert) borné (par la norme de T) du plan complexe, et donc un compact du plan. Ainsi, pour tout ouvert D tel que σ(T) ⊂ D, il existe un ensemble de courbes de Jordan lisses orientées positivement tel que σ(T) est à l'intérieur de Γ et que le complémentaire de D est contenu dans l'extérieur de Γ, ce qui justifie l'existence de l'intégrale définissant f(T).
Unicité de la définition
On va à présent montrer qu'avec les notations précédentes, f (T) ne dépend pas du choix de l'ensemble de courbes de Jordan Γ.
Un résultat préliminaire
Pour une collection de courbes de Jordan Γ = {γ1... γm} et un point a du plan complexe, l'indice de a par rapport à Γ est la somme des indices de a par rapport à chaque γi, ce que nous noterons n(a,Γ) = ∑i n(a,γi). Le théorème suivant est dû à Cauchy :
Théorème — Soit G ⊂ C un ouvert et Γ ⊂ G. Si g : C → C est holomorphe sur G, et si pour tout a du complémentaire deG, n(a, Γ) = 0, alors l'intégrale de contour ∫Γ g = 0.
L'analogue vectoriel de ce résultat, lorsque g prend ses valeurs dans L(X) et est holomorphe, se démontre en utilisant l'espace dual L(X)* de L(X), et en se ramenant au cas scalaire. En effet, considérons l'intégrale J=∫Γ g ∈ L(X). Si on peut montrer que, pour tout φ ∈ L(X)*, φ (∫Γ g) = 0, il en résultera que ∫Γ g = 0. φ étant borné, et l'intégrale étant normalement convergente, on a
Par composition, g étant supposée holomorphe, il en est de même de φ(g) : G ⊂ C → C. On peut donc lui appliquer le théorème de Cauchy (scalaire), obtenant
Démonstration de l'unicité
L'unicité de l'intégrale est une conséquence facile de ce qui précède. Soit D un ouvert contenant σ(T), Γ = {γi} et Ω = {ωj} deux ensembles finis de courbes de Jordan satisfaisant les hypothèses précédentes ; nous voulons montrer que
Notant Ω', l'ensemble obtenu à partir des courbes de Ω en renversant leur orientation ; on a
Les deux ensembles Γ ∪ Ω' et σ(T) sont compacts ; il existe donc un ouvert U contenant Γ ∪ Ω' tel que σ(T) soit contenu dans le complémentaire de U. Les points a du complémentaire de U ont pour indice n(a,Γ ∪ Ω') = 0 et la fonction est holomorphe sur U. La forme vectorielle du théorème de Cauchy donne donc
- ,
c'est-à-dire
ce qui montre l'unicité.
Il en résulte que si f1 et f2 sont deux fonctions holomorphes définies sur des voisinages D1 et D2 de σ(T), égales sur un ouvert contenant σ(T), alors f1(T) = f2(T). De plus, même si D1 est différent de D2, les opérateurs (f1 + f2) (T) et (f1·f2)(T) sont bien définis.
L'hypothèse d'holomorphie
Les résultats précédents n'ont pas encore utilisé pleinement l'hypothèse d'holomorphie de f sur un voisinage ouvert de σ(T). La convergence de l'intégrale demande seulement la continuité de f ; l'unicité est obtenue en supposant f holomorphe sur un voisinage de Γ ∪ Ω' ne contenant pas σ(T). La condition complète ne sera utilisée que pour démontrer que le calcul fonctionnel est un homomorphisme.
Propriétés
Le cas polynomial
La linéarité de l'application provient de la convergence de l'intégrale, et de ce que les opérations linéaires (somme et produit par un scalaire) d'un espace de Banach sont continues.
Pour montrer qu'on retrouve le calcul fonctionnel polynomial lorsque f(z) = ∑0 ≤ i ≤ m ai zi est un polynôme, il suffit de le montrer pour f(z) =zk (avec k ≥ 0), c'est-à-dire de montrer que pour un contour convenable Γ entourant σ(T). Prenant pour Γ un cercle de rayon plus grand que la norme de T, et représentant l'application résolvante par la série on obtient
- ;
échangeant série et intégrale (la convergence étant uniforme), on trouve effectivement
- (où δ est le symbole de Kronecker).
Homomorphisme
Pour des fonctions f1 et f2 satisfaisant l'hypothèse d'holomorphie, on a la propriété d'homomorphisme suivante :
La démonstration utilise la première formule de la résolvante. On commence par calculer directement
en choisissant Γ1 situé à l’intérieur de Γ2. Cette expression est égale à
Appliquant la formule de la résolvante, on obtient
Le second terme s'annule parce que ω ∈ Γ2 est à l'extérieur de Γ1 et que f1 est holomorphe sur un voisinage ouvert de σ(T). Ainsi,
Comme, d'après la formule de Cauchy (scalaire), , on a
Continuité pour la convergence sur les compacts
Soit G ⊂ C un ouvert tel que σ(T) ⊂ G, et {fk} une suite de fonctions holomorphes sur G convergeant uniformément sur tout compact inclus dans G. Alors {fk(T)} est une suite convergente de L(X). En effet (supposant pour simplifier que Γ ne contient qu'une courbe de Jordan), on a
Utilisant les hypothèses de convergence et de continuité, on voit que cette expression tend vers 0 lorsque k et l tendent vers l'infini. {fk(T)} est donc une suite de Cauchy, convergente puisque l'espace L(X) est complet.
Unicité du calcul fonctionnel holomorphe
En résumé, le calcul fonctionnel holomorphe, considéré comme une fonction (ou plutôt comme un opérateur) allant des fonctions holomorphes vers les opérateurs bornés : , possède les propriétés suivantes :
- Il étend le calcul fonctionnel polynomial.
- C'est un homomorphisme d'algèbres entre l'algèbre des fonctions holomorphes définies sur un voisinage de σ(T) et L(X).
- Il respecte la convergence uniforme sur les compacts.
On démontre qu'il n'existe qu'un seul calcul fonctionnel (un seul homomorphisme) ayant ces propriétés.
Dans tout ce qui précède, on peut remplacer l'algèbre des opérateurs bornés L(X) par une algèbre de Banach A quelconque ; on peut de même définir f (a) pour un élément a arbitraire de A (avec une définition convenable du spectre de a).
Considérations spectrales
On vient de voir que, dans le cas général, la définition d'un calcul fonctionnel holomorphe sur un opérateur T ∈ L(X) nécessite la connaissance de σ(T). Sous des hypothèses plus restrictives, il est réciproquement possible d'énoncer le théorème spectral (pour des opérateurs bornés) à l'aide d'un calcul fonctionnel. Cette section esquisse certains résultats allant dans cette direction.
Le théorème de l'application spectrale
On sait que le théorème de l'application spectrale (en) s'applique au calcul fonctionnel polynomial : pour tout polynôme p, on a σ(p(T)) = p(σ(T)). Ce résultat s'étend au calcul fonctionnel holomorphe, c'est-à-dire que pour toute fonction f holomorphe, on a σ(f(T)) = f(σ(T)). Pour montrer que f(σ(T)) ⊂ σ(f(T)), on remarque que si μ est un nombre complexe quelconque, il existe une fonction g holomorphe sur un voisinage de σ(T) telle que (c'est un résultat élémentaire d'analyse complexe). On en déduit (par homomorphisme) que f(T) - f(μ) = (T - μ)g(T) ; par conséquent, μ ∈ σ(T) implique f(μ) ∈ σ(f(T)).
Pour démontrer l'inclusion réciproque, supposons que μ ne soit pas dans f(σ(T)). On peut appliquer le calcul fonctionnel à , et donc g(T)(f(T) -μ) = I. Il en résulte que μ n'appartient pas à σ(f(T)).
Projections spectrales
Soit K un sous-ensemble de σ(T) et U etV des voisinages ouverts disjoints de K et de σ(T)\K respectivement. On pose e(z) = 1 si z ∈ U et e(z) = 0 si z ∈ V. La fonction e est holomorphe (sur U ∪ V) et vérifie [e(z)]2 = e(z) ; pour un contour Γ contenu dans U ∪ V et entourant σ(T), l'opérateur est donc un projecteur borné commutant avec T.
Les voisinages U et V existent si et seulement si K est à la fois ouvert et fermé pour la topologie induite sur σ(T) (autrement dit, si K est une réunion de composantes connexes de σ(T)). e étant nul sur V, sa contribution à l'intégrale l'est aussi. En résumé, pour tout ensemble K ouvert et fermé de σ(T), on définit un projecteur e(T), appelé la projection spectrale de T en K et noté P(K;T), par , où Γ est un contour entourant K mais aucun autre point de σ(T).
P = P(K;T) étant borné et commutant avec T, on peut exprimer T sous la forme A ⊕ B, avec A restriction de T à PX et B restriction de T à (1-P)X ; PX et (1-P)X sont des sous-espaces invariants par T, de plus, σ(A) = K et σ(B) = σ(T)\K. Une propriété importante de ces projecteurs est leur orthogonalité mutuelle : si L est un autre sous-ensemble ouvert et fermé de σ(T), P(K;T)P(L;T) = P(L;T)P(K;T) = P(K ∩ L;T), nul si K et L sont disjoints.
Les projections spectrales ont de nombreuses applications. Tout point isolé de σ(T) a une projection spectrale associée. En dimension finie, c'est le cas de tous les points de σ(T), et la décomposition correspondante de T est une variante de la forme normale de Jordan (les blocs de Jordan associés à une même valeur propre étant regroupés). Cette décomposition sera étudiée plus précisément dans la section suivante.
Les propriétés des projections spectrales découlent souvent de celles de l'opérateur projeté. Ainsi, si T est une matrice à coefficients positifs de rayon spectral r, le théorème de Perron-Frobenius affirme que r ∈ σ(T). La projection spectrale associée P = P(r;T) est également positive, et la propriété d'orthogonalité mutuelle montre qu'aucune autre projection spectrale ne peut avoir de ligne ou de colonne positive. En fait, TP = rP et (T/r)n tend vers P lorsque n tend vers l'infini, aussi P (appelé la projection de Perron) est une approximation de (T/r)n d'autant meilleure que n est grand, et chacune de ses colonnes est un vecteur propre de T.
Plus généralement, si T est un opérateur compact, les points non nuls de σ(T) sont isolés, et tout sous-ensemble fini de ces points peut être utilisé pour décomposer T ; les projections spectrales associées sont toutes de rang fini. Les opérateurs de L(X) dont le spectre a cette propriété sont appelés des opérateurs de Riesz. De nombreuses classes d'opérateurs de Riesz (y compris la classe des opérateurs compacts) sont des idéaux de L(X), et constituent un domaine de recherche actif. Cependant, si X est un espace de Hilbert, il n'existe qu'un seul idéal fermé entre les opérateurs de Riesz et les opérateurs de rang fini.
La discussion précédente peut en grande partie se généraliser au cas des algèbres de Banach. Les projections spectrales sont alors appelées des idempotents spectraux, car on ne peut plus en général définir un espace sur lesquelles elles se « projetteraient ».
Décomposition en sous-espaces invariants
Si le spectre σ(T) n'est pas connexe, X peut se décomposer en sous-espaces invariants par T en utilisant le calcul fonctionnel. Écrivant σ(T) comme union disjointe , définissons ei comme valant 1 sur un voisinage de la composante Fi et 0 sur des voisinages des autres composantes. ei(T) est donc la projection spectrale P(Fi;T) décrite dans la section précédente. La relation ei(T) T = T ei(T) montre que l'image de chaque ei(T), notée Xi, est un sous-espace invariant par T. Comme , X peut s'exprimer comme somme de ces sous-espaces : . De même, notant Ti la restriction de T à Xi, on a
Munissant la somme directe de la norme X' est un espace de Banach, et l'application R: X' → X définie par est un isomorphisme d'espaces de Banach ; on a . Cette écriture peut être vue comme une diagonalisation par blocs de T.
Si X est de dimension finie, σ(T) = {λi} est un ensemble fini de points du plan. Choisissant ei = 1 sur un disque ouvert ne contenant que λi, la matrice de blocs qui correspond à ce choix est alors la forme canonique de Jordan de la matrice T.
Généralisations
Avec des hypothèses plus fortes sur T, par exemple si T est un opérateur normal agissant sur un espace de Hilbert, on peut élargir le domaine du calcul fonctionnel au cas où f est seulement supposée continue sur σ(T) (obtenant le calcul fonctionnel continu (en)), ou même, utilisant la théorie de la mesure, au cas où f est seulement mesurable (obtenant le calcul fonctionnel borélien (en)). Dans ce dernier contexte, si E ⊂ σ(T) est un ensemble borélien et si E(x) est la fonction caractéristique de E, l'opérateur de projection E(T) a des propriétés analogues à celles des ei(T) discutés précédemment.
Le calcul fonctionnel borélien peut être étendu aux opérateurs auto-adjoints non bornés d'un espace de Hilbert.
De même que le calcul fonctionnel holomorphe peut être étendu à des éléments quelconques d'une algèbre de Banach, le calcul fonctionnel continu s'étend à tous les éléments normaux d'une C*-algèbre, et le calcul fonctionnel borélien à tous les éléments normaux d'une algèbre de von Neumann.
Opérateurs non bornés
Un calcul fonctionnel holomorphe analogue peut être défini pour tous les opérateurs fermés non bornés dont l'ensemble résolvant est non-vide.
Voir aussi
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Holomorphic functional calculus » (voir la liste des auteurs).
- (en) Nelson Dunford et Jacob T. Schwartz, Linear Operators, Part I: General Theory, Interscience, 1958.
- (en) Steven G Krantz, Dictionary of Algebra, Arithmetic, and Trigonometry. CRC Press, 2000. (ISBN 1-58488-052-X).










































![{\displaystyle ={\frac {1}{(2\pi i)^{2}}}\int _{\Gamma _{1}}f_{1}(\zeta )(\zeta -T)^{-1}\;\left[\int _{\Gamma _{2}}{\frac {f_{2}(\omega )}{\omega -\zeta }}d\omega \right]\;d\zeta -{\frac {1}{(2\pi i)^{2}}}\int _{\Gamma _{2}}f_{2}(\omega )(\omega -T)^{-1}\;\left[\int _{\Gamma _{1}}{\frac {f_{1}(\zeta )}{\omega -\zeta }}\,d\zeta \right]\;d\omega .}](https://img.franco.wiki/i/f7824e80471ad083de08ca3c950a3e35e9cc87e0.svg)
![{\displaystyle f_{1}(T)f_{2}(T)={\frac {1}{2\pi i}}\int _{\Gamma _{1}}f_{1}(\zeta )(\zeta -T)^{-1}\;\left[{\frac {1}{2\pi i}}\int _{\Gamma _{2}}{\frac {f_{2}(\omega )}{\omega -\zeta }}\,d\omega \right]\;d\zeta .}](https://img.franco.wiki/i/31abfa8aa47e1ece38b5231afaf91276e57942ab.svg)
















