Atoms in Molecules
L'approche Atoms in Molecules (AIM) ou Atoms in Molecules ou encore théorie quantique des atomes dans les molécules (en anglais Quantum Theory of Atoms in Molecules, QTAIM) est un modèle de chimie quantique caractérisant un système chimique en se basant sur une approche topologique de la densité électronique, issue du calcul ou de l'expérience. La théorie AIM permet notamment le calcul de certaines propriétés physiques en fournissant une définition topologique de la notion "d'atome", en divisant l'espace en volumes caractérisant cette notion (appelés bassins) contenant chacun exactement un noyau. Développée par le professeur Richard Bader dès le début des années 1960, elle est devenue progressivement dans les dernières décennies une théorie pour proposer des réponses à certaines questions sur les systèmes chimiques, dans de nombreux cas difficilement tractables par d'autres modèles ou théories en chimie[1]. Dans cette théorie, un atome est défini comme un système propre ouvert, c'est-à-dire un système pouvant transporter de l'énergie et de la densité électronique, localisé et connecté dans l'espace tridimensionnel par la notion de "points critiques".

Atomes de calcium en jaune,
en vert le fluor
en rouge le potassium.
La théorie "Atoms In Molecules"
Étude de la topologie de la densité électronique par la notion de "points critiques"
L'approche AIM se base sur l'étude de la topologie de la densité électronique et particulièrement sur celle des points critiques. Mathématiquement, ces derniers, de coordonnées représentent chacun un point dans l'espace en trois dimensions pour lesquels chacune des composantes du gradient de la densité électronique s'annule :
Cette dernière définition implique donc qu'un point critique est un point de la densité électronique correspondant localement soit à un minimum, soit à un maximum de la densité électronique, pouvant être associé à une situation chimique donnée. Ce lien peut très facilement être illustré dans le cas de la molécule de dihydrogène (figure 1) :
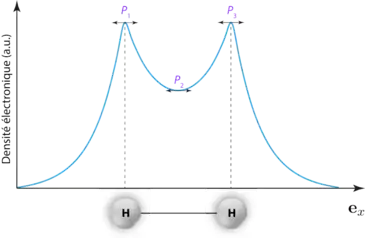
En une dimension, ici le long de l'axe , trois points critiques , et peuvent être déterminés avec et étant des maxima locaux et un minimum local de la densité électronique. Dans ce cas simple unidimensionnel, les maxima locaux peuvent donc être associés à des positions de noyaux tandis que le minimum local, entre deux atomes, peut être attribué à la liaison chimique entre les deux hydrogènes sans ambiguïté. Dans le cas général, étendu à l'espace en trois dimensions, la détermination des extremas locaux doit faire appel à la dérivée seconde de la densité électronique, soit le laplacien de cette dernière. Un point critique pouvant en effet très bien être un maximum local sur un axe donné et un minimum sur les deux autres (point selle). Ainsi, une classification des différents points critiques peut être réalisée via la diagonalisation de la matrice hessienne de la densité électronique :
La matrice hessienne étant de dimension 3 avec chaque colonne associée à l'un des axes de l'espace, une valeur propre positive désigne un minimum local sur celui-ci, une valeur propre négative, un maximum local sur ce dernier. Un point critique sera alors classé selon une notation type où représente la somme des courbures de la densité électronique selon les trois axes de l'espace (toujours égale à 3 lorsqu'une molécule est considérée dans une configuration nucléaire stable) et la somme des signes des trois valeurs propres de la matrice hessienne de la densité électronique. De cette façon, 4 types de points critiques sont définis dans la théorie AIM :
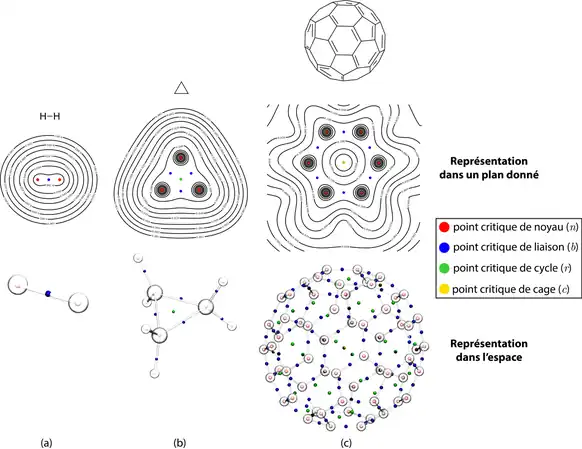
- Point critique de type , noté : trois valeurs propres négatives. Indique la présence d'un noyau atomique (indiqué dans le cas du dihydrogène, figure 2 (a)).
- Point critique de type , noté : une valeur propre positive et deux valeurs propres négatives. Indique la présence d'une liaison chimique (indiqué en figure 2).
- Point critique de type , noté : une valeur propre négative et deux valeurs propres positives. Indique la présence d'un cycle (indiqué dans le cas du cyclopropane et du fullerène, figure 2 (b, c)).
- Point critique de type , noté : trois valeurs propres positives. Indique la présence d'une cage (indiqué dans le cas du fullerène en figure 2 (c)).
Dans un système comprenant un nombre fini d'atomes, le nombre de points critiques est gouverné par la relation de Poincaré-Hopff :
Définition d'un atome et d'une molécule selon AIM
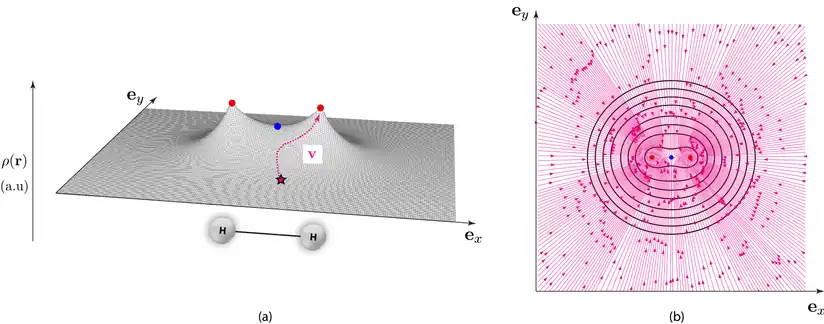
La densité électronique pouvant être exprimée en tout point d'une molécule donnée et dérivable, chacun de ces points peut aussi s'exprimer selon un vecteur gradient représentant la pente locale de la densité électronique. Ainsi, à partir d'un point quelconque de la densité électronique, en connaissance de son gradient, une trajectoire peut être définie dans la direction de plus grande pente vers des valeurs croissantes de densité électronique. Cette trajectoire aboutit toujours mathématiquement vers la position d'un point critique associé à la présence d'un noyau (figure 3 (a)) et correspond au flux électronique. L'ensemble de ces trajectoires représentent dans la théorie AIM des schémas appelés "portraits de phase" correspondant à la projection de ces dernières dans un plan considéré (figure 3 (b)).
AIM définit alors le bassin d'un "attracteur", ou tout simplement bassin la région de l'espace traversée par les trajectoires du vecteur gradient de la densité électronique aboutissant sur "l'attracteur" correspondant tout simplement à la présence d'un point critique de type indiquant la présence d'un noyau (figure 4).
De cette façon, un atome est alors défini selon AIM comme étant l'union du point critique lui étant associé et son bassin.
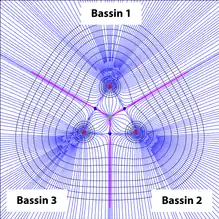
Dans le cas moléculaire, la limite entre les bassins est appelée surface interatomique et correspond à une zone où le flux électronique est nul (en magenta en figure 4). En d'autres termes, ces surfaces représentent des zones tridimensionnelles où le gradient de la densité électronique est nul. Ces zones sont conditionnées par la présence d'un point critique de type : ce sont des zones pour lesquelles les trajectoires du gradient de la densité électronique partant d'un point quelconque de l'espace convergent asymptotiquement vers celui-ci avant d'être déviées vers un point critique de type correspondant à la présence d'un noyau.
Chaque point critique de type indiquant la présence d'un noyau peut être associé à un autre point critique de même type par la présence d'un point critique de type , caractérisant l'existence d'une liaison chimique. La théorie AIM définit alors le terme de chemin de liaison caractérisant l'interaction de deux points critiques de type via un point critique de type . L'ensemble des chemins de liaison représente par la suite le graphique moléculaire fournissant la représentation schématique de la molécule considérée, la définition selon la théorie AIM d'une molécule (figure 5).
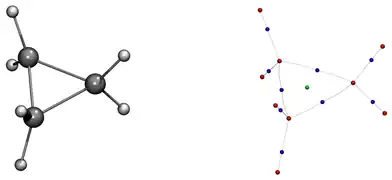
Applications qualitatives de la théorie AIM
Les principales constats de l'approche AIM sont :
- une molécule peut être divisée de manière unique en un ensemble de volumes atomiques. Ces volumes sont séparés par une série de surfaces au travers desquelles le champ vectoriel du gradient de densité électronique n'a pas de flux : . Les propriétés atomiques comme la charge atomique, le moment dipolaire et les énergies peuvent être calculées en intégrant les opérateurs correspondants sur le volume atomique.
- deux atomes sont liés si leurs volumes atomiques possèdent une interface interatomique commune, et qu'il existe un point critique (3, −1) sur cette surface. Un point critique est défini comme un point de l'espace où le gradient est nul. Un point critique (3, −1) est défini comme un point critique auquel deux des valeurs propres de la matrice hessienne pour ce point sont négatives et la densité électronique est un maximum par rapport à la ligne de voisinage. Au long du chemin viriel associé, l'énergie potentielle est maximalement stabilisée.
- les liaisons interatomiques sont classés soit comme confinée ou apportée, selon que le laplacien de la densité électronique au point critique soit positif ou négatif, respectivement.
- la tension géométrique de la liaison peut être évaluée en examinant la déviation du point critique liant à partir des axes interatomiques entre les deux atomes. Une déviation large implique une tension plus élevée.
Quelques applications quantitatives
La QTAIM est appliquée à la description de certains cristaux organiques présentant des distances inhabituellement courtes pour des molécules voisines comme observées par diffractométrie de rayons X. Ainsi, par exemple, dans la structure cristalline du chlore moléculaire, la distance Cl-Cl entre deux molécules est de 327 picomètres, plus faibles que la somme des rayons de Van der Waals (260 picomètres). Ainsi, la QTAIM prévoit douze chemins de liaison partant de chaque atome de chlore vers chaque autre atome de chlore, y compris l'autre atome de chlore dans la molécule. La théorie vise aussi à expliquer les propriétés métalliques de l'hydrogène métallique de manière quasi similaire.
La théorie est aussi appliquée à ce qu'on appelle les liaisons hydrogène-hydrogène[2] qui se produisent dans des molécules comme le phénanthrène ou le chrysène. Dans ces composés, la distance entre deux atomes d'hydrogène en position ortho est plus courte que leurs rayons de Van der Waals et selon des expériences numériques basées sur cette théorie, un chemin de liaison a été identifié entre eux. Les deux atomes d'hydrogène montrent des densités électroniques identiques et des couches proches, bien que très différentes de ce que l'on appelle des liaisons dihydrogène qui sont postulées pour des composés comme (CH3)2NHBH3 et aussi différentes des interactions agostiques.
En chimie « classique », la proximité immédiate de deux atomes non liés conduit à une répulsion stérique déstabilisante, mais en QTAIM les interactions hydrogène-hydrogène observées sont en fait stabilisantes. Il est de fait bien connu que les isomères « noués » phénanthrène et chrysène sont plus stables d'environ 6 kcal/mol que leurs isomères linéaires respectifs l'anthracène et le tétracène. Une explication « classique » est donnée par la règle de Clar. La QTAIM montre qu'une stabilisation de 8 kcal/mole se produit pour le phénanthrène, résultant du transfert électronique du carbone à l'hydrogène, décalé de 12,1 kcal/mol par rapport à la stabilisation due au chemin de la liaison H-H. La densité électronique au point critique entre les deux atomes d'hydrogène est faible, de 0,012 e− pour le phénanthrène. Une autre des propriétés du chemin de liaison est sa courbure.
Un autre exemple des molécules étudiées en QTAIM est le biphényle. Ses deux cycles phényle font un angle de 38° l'un par rapport à l'autre par rapport à la géométrie moléculaire plane (qui se rencontre lors de la rotation autour de la liaison C-C centrale) déstabilisée de 2,1 kcal/mol et par rapport à la géométrie perpendiculaire déstabilisée de 2,5 kcal/mol. L'explication classique de cette barrière de rotation sont les répulsions stériques entre les atomes d'hydrogène en ortho (plans) et la perte de la délocalisation de la densité électronique π sur les deux cycles (perpendiculaires).
En QTAIM, l'augmentation de l'énergie lors de la diminution de l'angle diédral de 38° à 0° est une somme de plusieurs facteurs. Les facteurs de déstabilisation sont l'augmentation de la longueur de liaison entre les atomes de carbone liants (puisqu'ils doivent réagir à l'approche des atomes d'hydrogène) et le transfert de charge électronique entre carbone et hydrogène. Les facteurs de stabilisation sont la délocalisation croissante des électrons π d'un cycle à l'autre et la liaison hydrogène-hydrogène entre les atomes hydrogènes ortho.
La nature de la liaison hydrogène-hydrogène et ses propriétés restent sujettes à questionnement. Selon certains, la stabilité relative du phénanthrène comparée à celle de son isomère peut être expliquée en comparant les stabilisations de résonance[3]. Une autre critique[4] émise indique que la stabilité du phénanthrène peut être attribuée à un recouvrement π-π plus effectif sur la double liaison centrale, l'existence de chemins de liaisons n'étant pas contestée au contraire de l'énergie de stabilisation dérivée.
Références
- Atoms in Molecules: A Quantum Theory de Richard Bader
- Hydrogen - Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals Cherif F. Matta, Jesus Hernandez-Trujillo, Ting-Hua Tang, Richard F. W. Bader Chem. Eur. J. 2003, 9, 1940 ± 1951 DOI 10.1002/chem.200204626
- Molecular Recognition in Organic Crystals: Directed Intermolecular Bonds or Nonlocalized Bonding? Jack D. Dunitz and Angelo Gavezzotti Angew. Chem. Int. Ed. 2005, 44, 1766 – 1787 DOI 10.1002/anie.200460157
- Polycyclic Benzenoids: Why Kinked is More Stable than Straight Jordi Poater, Ruud Visser, Miquel Sola, F. Matthias Bickelhaupt J. Org. Chem. 2007, 72, 1134-1142 DOI jo061637p
Liens externes
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Atoms in Molecules » (voir la liste des auteurs).








![{\displaystyle H(\rho (\mathbf {r} _{c}))={\begin{pmatrix}{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial x^{2}}}&{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial x\partial y}}&{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial x\partial z}}\\{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial y\partial x}}&{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial y^{2}}}&{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial y\partial z}}\\{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial z\partial x}}&{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial z\partial y}}&{\frac {\partial ^{2}\rho (\mathbf {r} _{c})}{\partial z^{2}}}\end{pmatrix}}{\xrightarrow[{}]{\textrm {diagonalisation}}}{\begin{pmatrix}\lambda _{1}&0&0\\0&\lambda _{2}&0\\0&0&\lambda _{3}\end{pmatrix}}.}](https://img.franco.wiki/i/c3f198cb306d46429d86a98eb6491b1b8ab006d6.svg)

















