Alignement de séquences

En bio-informatique, l'alignement de séquences (ou alignement séquentiel) est une manière de représenter deux ou plusieurs séquences de macromolécules biologiques (ADN, ARN ou protéines) les unes sous les autres, de manière à en faire ressortir les régions homologues ou similaires. L'objectif de l'alignement est de disposer les composants (nucléotides ou acides aminés) pour identifier les zones de concordance. Ces alignements sont réalisés par des programmes informatiques dont l'objectif est de maximiser le nombre de coïncidences entre nucléotides ou acides aminés dans les différentes séquences. Ceci nécessite en général l'introduction de « trous » à certaines positions dans les séquences, de manière à aligner les caractères communs sur des colonnes successives. Ces trous correspondent à des insertions ou des délétions (appelés indel) de nucléotides ou d'acides aminés dans les séquences biologiques. Le résultat final est traditionnellement représenté comme des lignes d'une matrice.

Alignement de séquences de récepteurs nucléaires. Les acides aminés conservés sont surlignés en bleu et en vert. Par endroits, on a inséré des trous, symbolisés par des tirets « - », pour permettre un alignement optimal

L'interprétation des alignements des séquences biologiques repose sur la théorie darwinienne de l'évolution. En général les séquences alignées correspondant à des molécules remplissant des fonctions similaires, il peut s'agir par exemple de la même enzyme chez différentes espèces, dont on suppose qu'elles dérivent d'un même ancêtre commun. Les divergences entre les séquences sont interprétées comme résultant de mutations. Les régions contenant des nucléotides ou des acides aminés conservés sont supposées correspondre à des zones où s'exerce une pression de sélection pour maintenir la fonction de la macromolécule.

L'alignement a plusieurs utilisations importantes en bioinformatique car il permet un certain nombre de prédictions. Il permet notamment d'identifier des sites fonctionnels (site catalytique, zone d'interaction...) qui correspondent en général aux régions les plus conservées, car ce sont elles sur lesquelles la pression de sélection est la plus grande. On peut aussi utiliser l'alignement de séquence pour prédire la ou les fonctions d'une protéine, si on détecte une homologie avec une protéine de fonction connue. Si la structure secondaire ou tertiaire de cette protéine de fonction homologue est connue, l'alignement peut être utilisé pour prédire la structure d'une protéine. Enfin, en cas d'alignements multiples au sein d'une famille de protéines, ceux-ci peuvent permettre d'établir une phylogénie entre elles.

Utilisation

Dans la compréhension du fonctionnement de la vie, les protéines jouent un rôle essentiel. On part donc de l'hypothèse que des protéines comportant des séquences similaires risquent fort de posséder des propriétés physico-chimiques identiques. À partir de l'identification de similarités entre la séquence d'une première protéine dont on connaît le mécanisme d'action et celle d'une deuxième protéine dont on ne connaît pas le mécanisme de fonctionnement, on peut inférer des similarités structurelles ou fonctionnelles sur la séquence non connue et proposer de vérifier de manière expérimentale le comportement d'action supposé.

Représentations

Les alignements sont habituellement représentés soit graphiquement soit en format texte. Dans la plupart des représentations des alignements séquentiels, les séquences sont écrites en lignes, disposées pour que les composantes communes apparaissent dans des colonnes successives. En format texte, les colonnes alignés contiennent des caractères identiques ou similaires, indiqués par un système cohérent de symboles. Un astérisque est utilisé pour montrer l'identité entre colonnes. Beaucoup de programmes utilisent de la couleur pour différencier l'information. Pour les ADN ou ARN, l'utilisation de couleur permet de différencier les nucléotides. Pour les alignements de protéines, elle permet d'indiquer les propriétés des acides aminés, ce qui aide à conclure sur la conservation du rôle d'un acide aminé substitué.

Lorsque plusieurs séquences sont mises en jeu, une dernière ligne est ajoutée pour conclure à un consensus.

On distingue deux types d'alignements qui diffèrent suivant leur complexité :

l'alignement par paires qui consiste à aligner deux séquences peut être réalisé grâce à un algorithme de complexité polynomiale. Il est possible de réaliser un alignement :
- global, c'est-à-dire entre les deux séquences sur toute leur longueur (exemple : algorithme de Needleman-Wunsch[1]) ;
- local, entre une séquence et une partie de l'autre séquence (exemple : algorithme de Smith-Waterman[2]) ;
l'alignement multiple, qui est un alignement global, consiste à aligner plus de deux séquences et nécessite un temps de calcul et un espace de stockage exponentiels en fonction de la taille des données.

Un alignement de séquence réalisé par ClustalW entre deux protéines humaines.

Les alignements séquentiels peuvent être fournis dans une large variété de formats de fichiers, dépendant par exemple du programme spécifique utilisé : FASTA, GenBank... Toutefois, dans les laboratoires de recherche, l'utilisation spécifique d'outils techniques peut réduire le choix de format.

Score et matrices de similarité

La plupart des méthodes d'alignement de séquences biologiques, et en particulier les méthodes d'alignement de séquence de protéines cherchent à optimiser un score d'alignement. Ce score est relié au taux de similarité entre les deux séquences comparées. Il tient compte d'une part du nombre d'acide aminés identiques entre les deux séquences et d'autre part du nombre d'acides aminés similaires sur le plan physico-chimique. Lorsque dans les deux séquences, on trouve ainsi alignés deux acides aminés très proches, comme Lysine (K) et Arginine (R), on parle de remplacement conservatif (les chaînes latérales de ces deux acides aminés portent toutes les deux une charge positive).

Ceci a nécessité la définition formelle d'un score d'identité ou de similarité entre deux acides aminés donnés. Ceci a donné naissance à des matrices de similarité, qui recensent l'ensemble des scores obtenus lorsque l'on substitue l'acide aminé à un autre. Il existe plusieurs de ces matrices avec des modes de construction différents. Ces matrices sont en général complétées par des fonctions de score pour quantifier l'introduction des indels dans les alignements.

Alignements locaux et globaux

l'alignement global tente d'aligner les séquences sur toute leur longueur, tandis que l'alignement local se focalise sur les zones de forte homologie.

Les méthodes d'alignement peuvent soit essayer d'aligner les séquences sur la totalité de leur longueur, on parle alors d'alignement global, soit se restreindre à des régions limitées dans lesquelles la similarité est forte, à l'exclusion du reste des séquences, on parle alors d'alignement local.

Les alignements globaux sont plus souvent utilisés quand les séquences mises en jeu sont similaires et de tailles comparables. Une technique générale, appelée algorithme de Needleman-Wunsch et basée sur la programmation dynamique, permet de réaliser des alignements globaux de manière optimale.

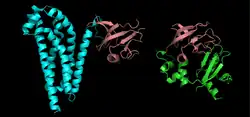
Exemple d'homologie locale entre protéines. Le domaine rouge brique est conservé entre ces deux protéines, mais le reste de la structure est différent

Lorsqu'il s'agit de séquences protéiques, il arrive cependant fréquemment que la région homologue soit limitée à une partie des séquences. C'est le cas lorsque deux protéines partagent un domaine homologue, associé à une fonction commune, mais que le reste de leurs séquences sont dissemblables (voir l'exemple sur la figure à droite). On utilise alors une méthode d'alignement local, comme l'algorithme de Smith-Waterman basé aussi sur la programmation dynamique, ou le programme BLAST, une méthode heuristique rapide permettant d'effectuer des recherches dans les bases de données. Les méthodes locales utilisent une méthode de calcul du score adaptée qui évite de pénaliser les régions non-homologues et ne calculent le score que sur la région conservée

Avec des séquences très voisines, les résultats obtenus par les méthodes d'alignement local ou global sont très proches. Pour cette raison, les méthodes d'alignement local, plus flexibles, sont plus souvent utilisées aujourd'hui. Elles permettent à la fois d'aligner des séquences localement ou globalement similaires.

Des méthodes hybrides, des méthodes semi-locales, s'avèrent utiles quand il s'agit de favoriser la mise en évidence de structures ou de zones fonctionnelles, habituellement masquées par la recherche du meilleur alignement (en termes de score).

Exemple :

         Score favorisé :      AGCTGCTATGATACCGACGAT
                               A--T-C-AT-A----------

         Alignement semi-local : AGCTGCTATGATACCGACGAT
                                 -------ATCATA--------

Malgré le « mismatch » pénalisant le score entre G et C, cet alignement montre une région conservée pouvant traduire une similarité de structure ou de fonction (malgré une petite mutation évolutive).

Alignement par paire

Les méthodes d'alignement par paires sont utilisées pour comparer des séquences deux à deux. Elles sont utilisées pour rechercher une homologie entre une séquence test et une séquence de référence, souvent extraite d'une base de données. Elles sont les plus simples à mettre en œuvre, et ce sont les seules pour lesquelles il existe des solutions algorithmiques optimales, basées sur la programmation dynamique. Il existe également des méthodes heuristiques rapides, qui permettent d'effectuer des recherches systématiques dans les banques de séquence. Dans ce cas, on compare une séquence inconnue à toutes les séquences de la base, en les testant successivement une par une.

Les méthodes les plus connues sont :

l'algorithme de Needleman-Wunsch[1] qui réalise l'alignement global optimal entre deux séquences ;
l'algorithme de Smith-Waterman[2] qui réalise un alignement local optimal.

Méthode par matrices de pixels

Dot-plot de la séquence d'un facteur de transcription humain contenant des doigts de zinc (GenBank ID NM_002383). La diagonale principale montre l'alignement de la séquence avec elle-même ; les diagonales secondaires montrent des répétitions internes du motif des doigts de zincs.

Les méthodes par matrices de pixels ou dot-plot, sont des méthodes graphiques de représentation des homologies entre deux séquences, mais ne sont pas à proprement parler des méthodes d'alignement. Les ressemblances ou homologies entre deux séquences données de longueur l et m sont représentées sous forme d'une matrice de pixels l x m. Chaque pixel de coordonnées (i, j) de la matrice est allumé ou éteint (noir ou blanc), en fonction d'une identité ou d'une homologie entre la position i de la première séquence et de la position j de la seconde séquence. Des techniques de filtrage ou de seuil sont souvent appliquées pour limiter le bruit de fond.

Dans cette représentation, les zones d'homologie de séquence apparaissent comme des segments diagonaux sur la matrice de pixels.

Alignement multiple

L'alignement multiple consiste à aligner collectivement un ensemble de séquences homologues, comme des séquences de protéines assurant des fonctions similaires dans différentes espèces vivantes. L'alignement multiple permet entre autres d'identifier les régions très conservées qui sont en général associées à des fonctions biologiques importantes, conservées dans l'Évolution.

Fonction de score

Pour réaliser un alignement multiple, il faut généraliser la notion de fonction de score définie plus haut pour deux séquences. En effet, on ne compare plus simplement les acides aminés ou les nucléotides deux à deux, mais à l'intérieur d'une colonne de l'alignement multiple. La généralisation de la fonction de score habituellement utilisée consiste donc à utiliser ce qu'on appelle le score de la somme des paires[3] au sein d'une colonne de l'alignement :

$Score(colonne)=\sum _{i<j}M(X_{i},X_{j})$

Où M correspond à la matrice de similarité et X_i et X_j correspondent aux acides aminés (ou nucléotides) se trouvant dans la colonne, au niveau des lignes i et j de l'alignement. Ce score inclut toutes les combinaisons deux à deux d'acides aminés (ou de nucléotides) dans la colonne, d'où la dénomination de "score de la somme des paires".

Méthodes progressives

Les méthodes progressives, hiérarchiques ou par arborescence génèrent un alignement final en plusieurs étapes. A chaque étape, une partie seulement des séquences est alignée, et ce n’est qu’à la fin que toutes les séquences se trouvent regroupées. La méthode utilisée classiquement pour déterminer l’ordre dans lequel doivent être alignées les séquences est basée sur le principe du Neighbour joining (NJ) . Pour cela, il faut réaliser les alignements par paire de tous les couples de séquences, afin de connaître leur degré de similarité. Il est ainsi possible de réaliser une matrice de “distances” entre toutes les séquences. Le Neighbor-Joining permet de créer un arbre, appelé Guide tree, qui détermine l’ordre dans lequel s’effectue l’alignement. Le chemin remontant des branches vers la racine indique quels sont les groupes de séquences à aligner, ainsi que l’ordre dans lequel doivent se faire les alignements.

Le plus connu des algorithmes progressifs est Clustal W . Son principe est basé sur l’algorithme de programmation dynamique appliqué à l’alignement de deux séquences. Chaque alignement une fois obtenu est converti en une unique séquence consensus, appelée profil. La création d’un profil se fait en fonction du contenu de chacune des colonnes de l’alignement. Un profil ainsi obtenu est considéré comme une séquence à part entière, et peut dés lors être réutilisé pour un nouvel alignement avec le même algorithme. Il peut être aligné avec une des séquences initiales, mais également avec un autre profil. Tous les nœuds internes constituant le guide tree représentent des profils

Les résultats de l'alignement progressif dépendent du choix des séquences "les plus apparentées" et peuvent donc être sensibles aux inexactitudes des alignements initiaux par paires. La plupart des méthodes d'alignement progressif de séquences multiples pondèrent en outre les séquences de l'ensemble de la requête en fonction de leur parenté, ce qui réduit la probabilité de faire un mauvais choix de séquences initiales et améliore donc la précision de l'alignement.

Un certain nombre de variations de l'implémentation progressive de Clustal sont utilisées pour les alignements de séquences multiples, la construction d'arbres phylogénétiques, et comme entrée pour la prédiction de la structure des protéines. Une variante plus lente mais plus précise de la méthode progressive est connue sous le nom de "T-Coffee" (Fonction objective de cohérence basée sur les arbres pour l'évaluation de l'alignement), qui dans un premier temps commence par générer une bibliothéque d’alignements. A partir de cette bibliothèque, chaque couple de résidus se voit attribuer une valeur en fonction du nombre de fois où ils ont été alignés. Cette méthode permet d’ éviter l’utilisation des matrices de coûts, dont les valeurs prévues pour le cas général, ne sont pas toujours adaptées.

Méthodes itératives

Alors que l'approche progressive (vue plus haut) consiste à aligner les séquences graduellement, la méthode dite itérative, elle, consiste à aligner toutes les séquences simultanément. Les méthodes itératives tentent d'améliorer la forte dépendance à l'égard de la précision des alignements initiaux par paires, qui est le point faible des méthodes progressives. Les méthodes itératives optimisent une Fonction objectif basée sur une méthode de score d'alignement sélectionnée en attribuant un alignement global initial, généralement de basse qualité. L'alignement est ensuite amélioré par une suite d'itérations jusqu'à ce que l'alignement ne puisse plus être amélioré.

Recherche de motif

La recherche de motifs, également connue sous le nom d'analyse de profil, construit des alignements de séquences multiples globaux qui tentent d'aligner de courts motifs de Séquences conservées parmi les séquences de l'ensemble de requêtes. Pour ce faire, on commence par construire un alignement global général de séquences multiples, après quoi les régions hautement conservées sont isolées et utilisées pour construire un ensemble de matrices de profil. La matrice de profil de chaque région conservée est organisée comme une matrice de notation, mais ses comptes de fréquence pour chaque acide aminé ou nucléotide à chaque position sont dérivés de la distribution des caractères de la région conservée plutôt que d'une distribution empirique plus générale. Les matrices de profil sont ensuite utilisées pour rechercher dans d'autres séquences les occurrences du motif qu'elles caractérisent.

Techniques issues de l'informatique

La Transformée de Burrows-Wheeler a été appliquée avec succès à l'alignement rapide de lectures courtes dans des outils populaires tels que Bowtie et BWA.

Alignement structurel

Notes et références

S. B. Needleman et C. D. Wunsch, « A general method applicable to the search for similarities in the amino acid sequence of two proteins », Journal of Molecular Biology, vol. 48, n^o 3,‎ 1^er mars 1970, p. 443–453 (ISSN 0022-2836, PMID 5420325, lire en ligne, consulté le 1^er avril 2017)
T. F. Smith, M. S. Waterman et W. M. Fitch, « Comparative biosequence metrics », Journal of Molecular Evolution, vol. 18, n^o 1,‎ 1^er janvier 1981, p. 38–46 (ISSN 0022-2844, PMID 7334527, lire en ligne, consulté le 1^er avril 2017)
Frédéric Dardel et François Képès, Bioinformatique. Génomique et post-génomique, Palaiseau, Éditions de l’École Polytechnique, 2002, 246 p. (ISBN 2-7302-0927-1, lire en ligne).

Voir aussi

Phylo, jeu vidéo conçu pour faire calculer des alignements multiples par crowdsourcing.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.