Algorithme de colonies de fourmis
Les algorithmes de colonies de fourmis (en anglais : ant colony optimization, ou ACO) sont des algorithmes inspirés du comportement des fourmis, ou d'autres espèces formant un superorganisme, et qui constituent une famille de métaheuristiques d’optimisation.

| Type |
|---|
Initialement proposé par Marco Dorigo et al. dans les années 1990[1] - [2], pour la recherche de chemins optimaux dans un graphe, le premier algorithme s’inspire du comportement des fourmis recherchant un chemin entre leur colonie et une source de nourriture. L’idée originale s'est depuis diversifiée pour résoudre une classe plus large de problèmes et plusieurs algorithmes ont vu le jour, s’inspirant de divers aspects du comportement des fourmis.
En anglais, le terme consacré à la principale classe d’algorithme est « Ant Colony Optimisation » (ACO). Les spécialistes réservent ce terme à un type particulier d'algorithme. Il existe cependant plusieurs familles de méthodes s'inspirant du comportement des fourmis. En français, ces différentes approches sont regroupées sous les termes : « algorithmes de colonies de fourmis », « optimisation par colonies de fourmis », « fourmis artificielles » ou diverses combinaisons de ces variantes.
Origine
L’idée originale provient de l’observation de l’exploitation des ressources alimentaires chez les fourmis. En effet, celles-ci, bien qu’ayant individuellement des capacités cognitives limitées, sont capables collectivement de trouver le chemin le plus court entre une source de nourriture et leur nid.
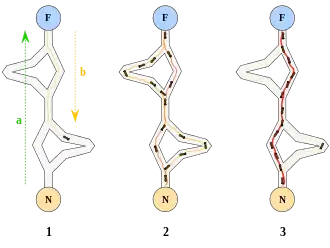
Des biologistes ont ainsi observé, dans une série d’expériences menées à partir de 1989[3] - [4], qu’une colonie de fourmis ayant le choix entre deux chemins d’inégale longueur menant à une source de nourriture avait tendance à utiliser le chemin le plus court.
Un modèle expliquant ce comportement est le suivant :
- une fourmi (appelée « éclaireuse ») parcourt plus ou moins au hasard l’environnement autour de la colonie ;
- si celle-ci découvre une source de nourriture, elle rentre plus ou moins directement au nid, en laissant sur son chemin une piste de phéromones ;
- ces phéromones étant attractives, les fourmis passant à proximité vont avoir tendance à suivre, de façon plus ou moins directe, cette piste ;
- en revenant au nid, ces mêmes fourmis vont renforcer la piste ;
- si deux pistes sont possibles pour atteindre la même source de nourriture, celle étant la plus courte sera, dans le même temps, parcourue par plus de fourmis que la longue piste ;
- la piste courte sera donc de plus en plus renforcée, et donc de plus en plus attractive ;
- la longue piste, elle, finira par disparaître, les phéromones étant volatiles ;
- à terme, l’ensemble des fourmis a donc déterminé et « choisi » la piste la plus courte.
Les fourmis utilisent leur environnement comme support de communication : elles échangent indirectement de l’information en déposant des phéromones, le tout décrivant l’état de leur « travail ». L’information échangée a une portée locale, seule une fourmi située à l’endroit où les phéromones ont été déposées y a accès. Ce système porte le nom de « stigmergie », et se retrouve chez plusieurs animaux sociaux (il a notamment été étudié dans le cas de la construction de piliers dans les nids de termites).
Le mécanisme permettant de résoudre un problème trop complexe pour être abordé par des fourmis seules est un bon exemple de système auto-organisé. Ce système repose sur des rétroactions positives (le dépôt de phéromone attire d’autres fourmis qui vont la renforcer à leur tour) et négatives (la dissipation de la piste par évaporation empêche le système de s'emballer). Théoriquement, si la quantité de phéromone restait identique au cours du temps sur toutes les branches, aucune piste ne serait choisie. Or, du fait des rétroactions, une faible variation sur une branche va être amplifiée et permettre alors le choix d’une branche. L'algorithme va permettre de passer d'un état instable où aucune branche n'est plus marquée qu'une autre, vers un état stable où l'itinéraire est formé des « meilleures » branches.
Exemple : le « système fourmi »
Description générale
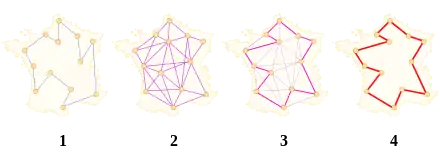
Le premier algorithme de colonies de fourmis proposé est appelé le Ant system[5] (système fourmi). Il vise notamment à résoudre le problème du voyageur de commerce, où le but est de trouver le plus court chemin permettant de relier un ensemble de villes.
L’algorithme général est relativement simple, et repose sur un ensemble de fourmis, chacune parcourant un trajet parmi ceux possibles. À chaque étape, la fourmi choisit de passer d’une ville à une autre en fonction de quelques règles :
- elle ne peut visiter qu’une fois chaque ville ;
- plus une ville est loin, moins elle a de chance d’être choisie (c’est la « visibilité ») ;
- plus l'intensité de la piste de phéromone disposée sur l’arête entre deux villes est grande, plus le trajet aura de chance d’être choisi ;
- une fois son trajet terminé, la fourmi dépose, sur l’ensemble des arêtes parcourues, plus de phéromones si le trajet est court ;
- les pistes de phéromones s’évaporent à chaque itération.
Description formelle
La règle de déplacement, appelée « règle aléatoire de transition proportionnelle », est écrite mathématiquement sous la forme suivante :
où Jk
i est la liste des déplacements possibles pour une fourmi k lorsqu’elle se trouve sur une ville i, ηij la visibilité, qui est égale à l’inverse de la distance de deux villes i et j (1/dij) et τij(t) l’intensité de la piste à une itération donnée t. Les deux principaux paramètres contrôlant l’algorithme sont α et β, qui contrôlent l’importance relative de l’intensité et de la visibilité d’une arête.
En pratique, pour que les fourmis explorent des pistes non découvertes, on attribue une probabilité non nulle d'exploration de ces villes « inconnues », contrôlée par le paramètre γ. De cette façon, la probabilité de déplacement s'écrit:
Une fois la tournée des villes effectuée, une fourmi k dépose une quantité de phéromone sur chaque arête de son parcours :
où Tk(t) est la tournée faite par la fourmi k à l’itération t, Lk(t) la longueur du trajet et Q un paramètre de réglage.
À la fin de chaque itération de l’algorithme, les phéromones déposées aux itérations précédentes par les fourmis s’évaporent de
Et à la fin de l'itération, on a la somme des phéromones qui ne se sont pas évaporées et de celles qui viennent d'être déposées :
où m est le nombre de fourmis utilisées pour l’itération t et ρ un paramètre de réglage.
Principales variantes
L’algorithme de colonies de fourmis a été à l’origine surtout utilisé pour produire des solutions quasi-optimales au problème du voyageur de commerce, puis, plus généralement, aux problèmes d’optimisation combinatoire. On observe que depuis ses débuts son emploi s'est étendu à plusieurs domaines, depuis l’optimisation continue jusqu’à la classification ou encore le traitement d’images.
Le cadre « ACO »
Une partie des algorithmes (notamment ceux conçus par M. Dorigo et ses collègues) sont maintenant regroupés sous le terme de « Ant Colony Optimisation » (ACO). Ce cadre se limite cependant aux algorithmes construisant des solutions sous la forme de paramètres associés aux composants d'un graphe, à l'aide d'un modèle statistique biaisé.
Une méthode de type ACO suit le schéma algorithmique suivant, paramétré par :
- un critère d'arrêt de l’algorithme
- un temps de calcul ou un nombre d'itérations alloué dépassé, un seuil d'amélioration des solutions qui n’est plus satisfaisant, ou une combinaison de critères
- des heuristiques
- (éventuellement) un critère de choix des pistes à explorer ou à éliminer, ...
- une construction des solutions et des pistes de phéromones
- dépendant du problème à résoudre et de sa structure
Initialisation des pistes de phéromone ; Boucler tant que critère d'arrêt non atteint : construire les solutions composant par composant, utilisation (facultative) d'une heuristique, mise à jour des pistes de phéromone ; Fin de la boucle.
Une variante efficace du système formique est le Max-Min Ant System (MMAS)[6], où seules les meilleures fourmis tracent des pistes et où le dépôt de phéromones est limité par une borne supérieure (empêchant une piste d’être trop renforcée) et une borne inférieure (laissant la possibilité d’être explorée à n’importe quelle solution). Cet algorithme atteint de meilleurs résultats que l’original, et évite notamment une convergence prématurée.
L’autre variante la plus connue est le Ant Colony System (ACS)[7], où à une nouvelle règle de déplacement (appelée « règle pseudo-aléatoire proportionnelle ») s’ajoute un processus de mise à jour « locale » des éléments des pistes de phéromones, l’objectif de ce mécanisme étant d’augmenter la diversification de la recherche.
Il est possible, pour certaines versions, de prouver que l’algorithme est convergent (c’est-à-dire qu’il est capable de trouver l’optimum global en un temps fini). La première preuve de convergence d'un algorithme de colonies de fourmis fut apportée en 2000, pour l’algorithme graph-base ant system, puis pour les algorithmes ACS et MMAS. Comme pour la plupart des métaheuristiques, il est très difficile d’estimer théoriquement la vitesse de convergence.
En 2004, Zlochin et ses collègues ont montré[8] que les algorithmes de type ACO pouvaient être assimilés aux méthodes de descente stochastique de gradient, d'entropie croisée et des algorithmes à estimation de distribution. Ils ont proposé de regrouper ces métaheuristiques sous le terme de « recherche à base de modèle ».
Une définition difficile
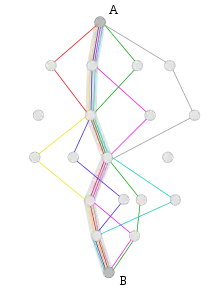
Il n’est pas facile de donner une définition précise de ce qu’est ou ce que n’est pas un algorithme de colonies de fourmis, car la définition peut varier selon les auteurs et les usages.
D’une façon très générale, les algorithmes de colonies de fourmis sont considérés comme des métaheuristiques à population, où chaque solution est représentée par une fourmi se déplaçant sur l’espace de recherche. Les fourmis marquent les meilleures solutions, et tiennent compte des marquages précédents pour optimiser leur recherche.
On peut les considérer comme des algorithmes multi-agents probabilistes, utilisant une distribution de probabilité implicite pour effectuer la transition entre chaque itération. Dans leurs versions adaptées à des problèmes combinatoires, ils utilisent une construction itérative des solutions.
D’après certains auteurs, ce qui différencierait les algorithmes de colonies de fourmis d’autres métaheuristiques proches (telles que les algorithmes à estimation de distribution ou l’optimisation par essaim particulaire) serait justement son aspect constructif. En effet, dans les problèmes combinatoires, il est possible que la meilleure solution finisse par être trouvée, alors même qu’aucune fourmi ne l’aura éprouvée effectivement. Ainsi, dans l’exemple du problème du voyageur de commerce, il n’est pas nécessaire qu’une fourmi parcoure effectivement le chemin le plus court : celui-ci peut être construit à partir des segments les plus renforcés des meilleures solutions. Cependant, cette définition peut poser problème dans le cas des problèmes à variables réelles, où aucune structure du voisinage n’existe.
Le comportement collectif des insectes sociaux reste une source d’inspiration pour les chercheurs. La grande diversité d’algorithmes (pour l’optimisation ou non) se réclamant de l’auto-organisation dans les systèmes biologiques a donné lieu au concept d’« intelligence en essaim », qui est un cadre très général, dans lequel s’inscrivent les algorithmes de colonies de fourmis.
Algorithmes stigmergiques
On observe en pratique qu’un grand nombre d’algorithmes se réclament d’une inspiration « colonies fourmis », sans toujours partager le cadre général de l’optimisation par colonies de fourmis canonique (ACO). En pratique, l’utilisation d’un échange d’informations entre fourmis via l’environnement (principe dénommé « stigmergie ») suffit à rentrer dans la catégorie des algorithmes de colonies de fourmis. Ce principe a mené certains auteurs à créer le terme d’« optimisation stigmergique »[9].
On trouve ainsi des méthodes s’inspirant de comportements de recherche de nourriture, de tri de larves, de division du travail ou de transport coopératif.
Applications
Les variantes combinatoires peuvent avoir un avantage, par rapport aux autres métaheuristiques, dans le cas où le graphe étudié peut changer dynamiquement au cours de l’exécution : la colonie de fourmis s’adaptera de façon relativement flexible aux changements. Ceci semble être intéressant pour le routage réseau[10].
Les algorithmes de colonies de fourmis ont été appliqués à un grand nombre de problèmes d’optimisation combinatoire, allant de l'affectation quadratique au repli de protéine ou au routage de véhicules. Comme beaucoup de métaheuristiques, l’algorithme de base a été adapté aux problèmes dynamiques, en variables réelles, aux problèmes stochastiques, multi-objectifs ou aux implémentations parallèles, etc.
Historique

Chronologie des algorithmes de colonies de fourmis.
- 1959, Pierre-Paul Grassé invente la théorie de la stigmergie pour expliquer le comportement de construction du nid chez des termites[11] ;
- 1983, Deneubourg et ses collègues étudient le comportement collectif des fourmis[12] ;
- 1988, Moyson et Manderick présentent un article sur l’auto-organisation chez les fourmis[13] ;
- 1989, travaux de Goss, Aron, Deneubourg et Pasteels, sur le comportement collectifs des fourmis Argentines, qui donneront l’idée des algorithmes de colonies de fourmis[3] ;
- 1989, implémentation d’un modèle de comportement de recherche de nourriture par Ebling et ses collègues[14] ;
- 1991, M. Dorigo propose le Ant System dans sa thèse de doctorat (qui ne sera publiée qu’en 1992[2]). Il fait paraître, avec V. Maniezzo et A. Colorni, un rapport technique[15], qui sera publié cinq ans plus tard[5] ;
- 1995, Bilchev et Parmee publient la première tentative d'adaptation aux problèmes continus[16] ;
- 1996, publication de l'article sur le Ant System[5] ;
- 1996, Stützle et Hoos inventent le MAX-MIN Ant System[6] ;
- 1997, Dorigo et Gambardella publient le Ant Colony System[7] ;
- 1997, Schoonderwoerd et ses collègues conçoivent la première application aux réseaux de télécommunications[17] ;
- 1997, Martinoli et ses collègues s’inspirent des algorithmes de colonies de fourmis pour le contrôle de robots[18] ;
- 1998, Dorigo lance la première conférence consacrée aux algorithmes de colonies de fourmis[19] ;
- 1998, Stützle propose les premières implémentations parallèles[20] ;
- 1999, Bonabeau et ses collègues font paraître un livre traitant principalement des fourmis artificielles[21] ;
- 1999, premières applications pour le routage de véhicule, le problème d'affectation (dans sa variante du problème d'affectation quadratique (en)), le sac à dos multi-dimensionnel ;
- 2000, numéro spécial d’une revue scientifique sur les algorithmes de colonies de fourmis[22] ;
- 2000, premières applications à l’ordonnancement, l’ordonnancement séquentiel, la satisfaction de contraintes ;
- 2000, Gutjahr donne la première preuve de convergence pour un algorithme de colonies de fourmis[23] ;
- 2001, première utilisation des algorithmes de colonies de fourmis par des entreprises (Eurobios et AntOptima) ;
- 2001, Iredi et ses collègues publient le premier algorithme multi-objectif[24] ;
- 2002, premières applications à la conception d’emploi du temps, les réseaux bayésiens ;
- 2002, Bianchi et ses collègues proposent le premier algorithme pour problème stochastique (en)[25] ;
- 2004, Zlochin et Dorigo montrent que certains algorithmes sont équivalents à la descente stochastique de gradient, l'entropie croisée et les algorithmes à estimation de distribution[8] ;
- 2005, premières applications au repliement des protéines.
- 2012, Prabhakar et ses collègues publient des travaux relatifs à la communication en tandem de fourmis sans phéromones, reflétant les principes d'organisation de réseau informatique. Le modèle de communication a été comparé au Transmission Control Protocol[26].
Sources
- (en) M. Dorigo, M. Birattari, T. Stützle, Ant Colony Optimization : Artificial Ants as a Computational Intelligence Technique, IEEE Computational Intelligence Magazine, volume 1, numéro 4, pages 28–39, 2006.
- (fr) Johann Dréo, Alain Petrowski, Éric Taillard, Patrick Siarry, Métaheuristiques pour l’optimisation difficile, 2003 extrait concernant les algorithmes de colonies de fourmis.
- (en) Éric Bonabeau, Marco Dorigo et Guy Theraulaz, Swarm Intelligence: From Natural to Artificial Systems, Oxford University Press, 1999. (ISBN 0195131592)
- (en) Marco Dorigo et Thomas Stützle, Ant Colony Optimization, Cambridge, MA, MIT Press/Bradford Books, 2004. (ISBN 0262042193)
- (fr) Nicolas Monmarché, Frédéric Guinand et Patrick Siarry (sous la dir.), Fourmis artificielles, Traité Informatique et Systèmes d'Information - IC2, Hermes, , Volume 1 (Des bases de l'optimisation aux applications industrielles), 333 p. 16x24 Relié, (ISBN 978-2-7462-2119-2). et Volume 2 (Nouvelles directions pour une intelligence collective), 323 p. 16x24 Relié, (ISBN 978-2-7462-2349-3).
- (fr) Christine Solnon. Optimisation par colonies de fourmis, Hermes-Lavoisier, aout 2008, 192 p. (ISBN 978-2-7462-1863-5).
Notes et références
- A. Colorni, M. Dorigo et V. Maniezzo, Distributed Optimization by Ant Colonies, actes de la première conférence européenne sur la vie artificielle, Paris, France, Elsevier Publishing, 134-142, 1991.
- M. Dorigo, Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italie, 1992.
- S. Goss, S. Aron, J.-L. Deneubourg et J.-M. Pasteels, The self-organized exploratory pattern of the Argentine ant, Naturwissenschaften, volume 76, pages 579-581, 1989.
- J.-L. Deneubourg, S. Aron, S. Goss et J.-M. Pasteels, The self-organizing exploratory pattern of the Argentine ant, Journal of Insect Behavior, volume 3, page 159, 1990.
- M. Dorigo, V. Maniezzo, et A. Colorni, Ant system: optimization by a colony of cooperating agents, IEEE Transactions on Systems, Man, and Cybernetics--Part B, volume 26, numéro 1, pages 29-41, 1996.
- T. Stützle et H.H. Hoos, MAX MIN Ant System, Future Generation Computer Systems, volume 16, pages 889-914, 2000.
- M. Dorigo et L.M. Gambardella, Ant Colony System : A Cooperative Learning Approach to the Traveling Salesman Problem, IEEE Transactions on Evolutionary Computation, volume 1, numéro 1, pages 53-66, 1997.
- M. Zlochin, M. Birattari, N. Meuleau, et M. Dorigo, Model-based search for combinatorial optimization: A critical survey, Annals of Operations Research, vol. 131, p. 373-395, 2004.
- A. Ajith; G. Crina; R. Vitorino (éditeurs), Stigmergic Optimization, Studies in Computational Intelligence, volume 31, 299 pages, 2006. (ISBN 978-3-540-34689-0).
- K. M. Sim, W. H. Sun, Ant colony optimization for routing and load-balancing : survey and new directions, IEEE Transactions on Systems, Man and Cybernetics, Part A, volume 33, numéro 5, pages 560-572, 2003.
- P.-P. Grassé, La reconstruction du nid et les coordinations inter-individuelles chez Belicositermes natalensis et Cubitermes sp. La théorie de la Stigmergie : Essai d’interprétation du comportement des termites constructeurs, Insectes Sociaux, numéro 6, p. 41-80, 1959.
- J.L. Denebourg, J.M. Pasteels et J.C. Verhaeghe, Probabilistic Behaviour in Ants : a Strategy of Errors?, Journal of Theoretical Biology, numéro 105, 1983.
- F. Moyson, B. Manderick, The collective behaviour of Ants : an Example of Self-Organization in Massive Parallelism, Actes de AAAI Spring Symposium on Parallel Models of Intelligence, Stanford, Californie, 1988.
- M. Ebling, M. Di Loreto, M. Presley, F. Wieland, et D. Jefferson, An Ant Foraging Model Implemented on the Time Warp Operating System, Proceedings of the SCS Multiconference on Distributed Simulation, 1989.
- Dorigo M., V. Maniezzo et A. Colorni, Positive feedback as a search strategy, rapport technique numéro 91-016, Dip. Elettronica, Politecnico di Milano, Italy, 1991.
- G. Bilchev et I. C. Parmee, The Ant Colony Metaphor for Searching Continuous Design Spaces, Proceedings of the AISB Workshop on Evolutionary Computation. Terence C. Fogarty (éditeurs), Evolutionary Computing Springer-Verlag, pages 25-39, avril 1995.
- R. Schoonderwoerd, O. Holland, J. Bruten et L. Rothkrantz, Ant-based load balancing in telecommunication networks, Adaptive Behaviour, volume 5, numéro 2, pages 169-207, 1997.
- A. Martinoli, M. Yamamoto, et F. Mondada, On the modelling of bioinspired collective experiments with real robots, Fourth European Conference on Artificial Life ECAL-97, Brighton, Royaume-Uni, juillet 1997.
- M. Dorigo, ANTS’ 98, From Ant Colonies to Artificial Ants : First International Workshop on Ant Colony Optimization, ANTS 98, Bruxelles, Belgique, octobre 1998.
- T. Stützle, Parallelization Strategies for Ant Colony Optimization, Proceedings of PPSN-V, Fifth International Conference on Parallel Problem Solving from Nature, Springer-Verlag, volume 1498, pages 722-731, 1998.
- É. Bonabeau, M. Dorigo et G. Theraulaz, Swarm intelligence, Oxford University Press, 1999.
- M. Dorigo, G. Di Caro et T. Stützle, special issue on “Ant Algorithms”, Future Generation Computer Systems, volume 16, numéro 8, 2000.
- W.J. Gutjahr, A graph-based Ant System and its convergence, Future Generation Computer Systems, volume 16, pages 873-888, 2000.
- S. Iredi, D. Merkle et M. Middendorf, Bi-Criterion Optimization with Multi Colony Ant Algorithms, Evolutionary Multi-Criterion Optimization, First International Conference (EMO’01), Zurich, Springer Verlag, pages 359-372, 2001.
- L. Bianchi, L.M. Gambardella et M.Dorigo, An ant colony optimization approach to the probabilistic traveling salesman problem, PPSN-VII, Seventh International Conference on Parallel Problem Solving from Nature, Lecture Notes in Computer Science, Springer Verlag, Berlin, Allemagne, 2002.
- Balaji Prabhakar, Katherine N. Dektar et Deborah M. Gordon, « The Regulation of Ant Colony Foraging Activity without Spatial Information », PLOS Comput Biol, vol. 8, , e1002670 (ISSN 1553-7358, PMID 22927811, PMCID 3426560, DOI 10.1371/journal.pcbi.1002670, lire en ligne, consulté le )
Voir aussi
Articles connexes
- Insectes sociaux, Intelligence collective, Système complexe.
- Algorithmes à estimation de distribution, descente stochastique de gradient, Entropie croisée, algorithmes équivalents au formalisme ACO.
- Optimisation par essaims particulaires, Algorithme évolutionnaire, méthodes similaires.
Liens externes
- (en) Ant Colony Optimization Home Page, site maintenu par Marco Dorigo, bibliographie, codes sources.
- (en)Une introduction aux algorithmes de colonies de fourmis (version archivée par Internet Archive)
- (en)« Une liste de références bibliographiques sur les fourmis artificielles »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)
- (en) ANT Colony Algorithm Une simulation en Java de l'algorithme de colonies de fourmis avec terrain modifiable. Présentation, dossier et code source téléchargeables.
- (fr) Application d'un algorithme de colonie de fourmis au problème du voyageur de commerce





