Algorithme à estimation de distribution
Les algorithmes à estimation de distribution (Estimation of Distribution Algorithms, EDA, en anglais) forment une famille de métaheuristiques inspirée des algorithmes génétiques. Ils sont utilisés pour résoudre des problèmes d'optimisation, via la manipulation d'un échantillonnage de la fonction décrivant la qualité des solutions possibles. Comme toutes les métaheuristiques utilisant une population de points, ils sont itératifs.

À l'inverse des algorithmes évolutionnaires « classiques », le cœur de la méthode consiste à estimer les relations entre les différentes variables d'un problème d'optimisation, grâce à l'estimation d'une distribution de probabilité, associée à chaque point de l'échantillon. Ils n'emploient donc pas d'opérateurs de croisement ou de mutation, l'échantillon étant directement construit à partir des paramètres de distribution, estimés à l'itération précédente.
Algorithme
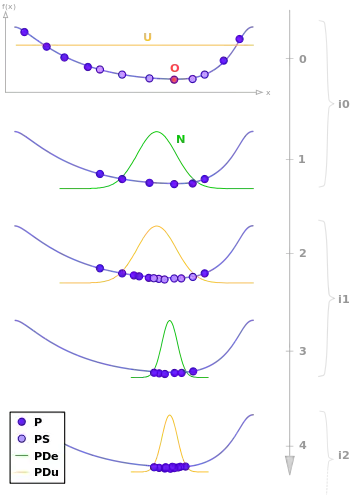
Le vocabulaire lié aux algorithmes à estimation de distribution est emprunté à celui des algorithmes évolutionnaires, on parlera donc de « population d'individus » plutôt que d'« échantillon de points », ou de « fitness » plutôt que de « fonction objectif », néanmoins, tous ces termes ont la même signification.
Algorithme général
L'algorithme de base procède de la manière suivante pour chaque itération :
- tirage aléatoire d'un ensemble de points suivant une distribution de probabilité donnée,
- sélection des meilleurs points,
- extraction des paramètres de la distribution de probabilité décrivant la répartition de ces points.
Plus précisément, l'algorithme procède comme suit :
Tirer au hasard M individus, pour former une population D0.
i = 0
Tant qu'un critère d'arrêt n'est pas vérifié :
i = i + 1
Sélectionner N individus (avec N < M) dans la population précédente (Di-1), pour former la population :.
Estimer une distribution de probabilité Pi(x), décrivant la répartition de la population DS
i-1.
Tirer au hasard M individus dans Pi(x).
Fin de la boucle.
Exemple pour le problème « one max »
Dans le problème du « one max », on cherche à maximiser le nombre de 1 sur un nombre de dimensions donné. Pour un problème à 3 dimensions, une solution x1 = {1,1,0} aura donc une meilleure qualité qu'une solution x2 = {0,1,0} , l'optimum étant i* = {1,1,1} . On cherche donc à maximiser une fonction , où xi peut prendre la valeur 0 ou 1.
La première étape consiste à tirer au hasard les individus, avec pour chaque variable, une chance sur deux de tirer un 1 ou un 0. Dit autrement, on utilise une distribution de probabilité , où p0(xi) est la probabilité que chaque élément soit égal à 1. La distribution est donc factorisée comme un produit de 3 distributions marginales univariantes de Bernoulli, de paramètre 0,5.
Exemple de tirage de la population D0, avec une population de 6 individus, la dernière ligne indique la probabilité p(x) pour chaque variable :
| i | x1 | x2 | x3 | f(x) |
| 1 | 0 | 1 | 0 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 1 | 0 | 1 | 2 |
| 4 | 1 | 0 | 1 | 2 |
| 5 | 0 | 1 | 1 | 2 |
| 6 | 1 | 0 | 0 | 1 |
| p(x) | 0.5 | 0.5 | 0.5 | |
L'étape suivante consiste en la sélection des meilleurs individus, pour former DS
1. Dans notre exemple, il s'agit simplement de ne garder que les 3 meilleurs individus :
| i | x1 | x2 | x3 | f(x) |
| 3 | 1 | 0 | 1 | 2 |
| 4 | 1 | 0 | 1 | 2 |
| 5 | 0 | 1 | 1 | 2 |
| p(x) | 0.7 | 0.3 | 1 | |
On constate que les trois paramètres (pi(x)) caractérisant la distribution de probabilité (DS
1) ont changé après la sélection. En utilisant cette nouvelle distribution, on peut tirer une nouvelle population :
| i | x1 | x2 | x3 | f(x) |
| 1 | 1 | 1 | 1 | 3 |
| 2 | 0 | 1 | 1 | 2 |
| 3 | 1 | 0 | 1 | 2 |
| 4 | 1 | 0 | 1 | 2 |
| 5 | 1 | 0 | 1 | 2 |
| 6 | 0 | 0 | 1 | 1 |
| p(x) | 0.7 | 0.3 | 1 | |
Et ainsi de suite jusqu'à vérifier un critère d'arrêt (par exemple quand tous les individus sont à l'optimum, comme l'individu 1 du tableau ci-dessus).
Comportement
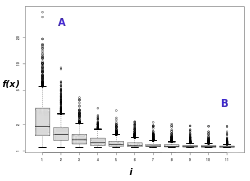
Il a été démontré (généralement à l'aide de modèles de Markov ou de systèmes dynamiques) que la plupart des versions pour l'optimisation combinatoire sont convergentes (c’est-à-dire qu'elles peuvent trouver l'optimum en un temps fini). Pour les variantes traitant de l'optimisation en variables réelles, la convergence est encore plus facile à démontrer, pour peu que les modèles de distributions utilisées permettent l'ergodicité (c’est-à-dire qu'il est alors possible d'atteindre n’importe quelle solution à chaque mouvement), mais on se satisfait souvent d’une quasi-ergodicité (si la métaheuristique peut atteindre n’importe quelle solution en un nombre fini de mouvements).
Modèles de distributions
Le comportement des algorithmes à estimation de distribution repose en grande partie sur le choix du modèle de distribution utilisé pour décrire l'état de la population. Pedro Larrañaga et ses collègues proposent de classer ces modèles en fonction de leur degré de prise en compte des dépendances entre les variables :
- modèles sans dépendances,
- modèles avec dépendances bi-variantes,
- modèles avec dépendances multi-variantes.
Dans le cas des modèles sans dépendances, la distribution de probabilité est construite à partir d'un ensemble de distributions définies sur une seule variable. Dit autrement, la distribution est factorisée à partir de distributions univariantes, indépendantes sur chaque variable.
L'exemple donné plus haut pour le problème du « one max » rentre dans cette catégorie : la probabilité d'avoir un 1 dans la variable x2 n'influence pas la probabilité d'avoir un 1 dans la variable x3, il n'y a aucune corrélation entre les deux variables.
Les modèles sans dépendances sont simples à manipuler, mais ils ont le défaut d'être peu représentatifs des problèmes d'optimisation difficile, où les dépendances sont souvent nombreuses. Il est possible de traiter les dépendances en dehors du modèle de distribution, mais l'algorithme peut alors devenir plus délicat à manipuler.
Dans le type des modèles à dépendances bi-variantes, il est possible d'utiliser des distributions bi-variantes comme base. Larrañaga et coll. proposent alors de classer l'apprentissage dans la notion de structure.
Dans les modèles à dépendances multi-variantes, toutes les dépendances sont prises en compte dans le modèle.
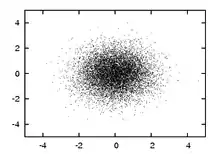 Exemple d'échantillon produit à partir d'une distribution normale bi-variante sans covariance. |
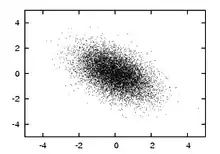 Exemple d'échantillon produit à partir d'une distribution normale bi-variante avec une covariance de -0.5. |
Le monde de l'estimation de distribution
Historique
- 1965 : Rechenberg conçoit le premier algorithme utilisant des stratégies d'évolution[1].
- 1975 : travaillant sur les automates cellulaires, Holland propose les premiers algorithmes génétiques[2].
- 1990 : Les algorithmes de colonie de fourmis sont proposées par Marco Dorigo, dans sa thèse de doctorat[3].
- 1994 : S. Baluja s'inspire des algorithmes évolutionnaires et propose l’apprentissage incrémental à population (« Population Based Incremental Learning », PBIL)[4].
- 1996 : Mühlenbein et Paaß proposent les algorithmes à estimation de distribution[5].
Variantes
Les variantes les plus connues de l'estimation de distribution sont l'apprentissage incrémental à population (« Population Based Incremental Learning », PBIL), l'algorithme à distribution marginale univariée (« Univariate Marginal Distribution Algorithm », UMDA) ou encore l'algorithme génétique compact (« Compact Genetic Algorithm », CGA).
Il existe également des variantes utilisant des mécanismes de partitionnement de données pour l'optimisation multimodale, des adaptations au calcul parallèle, etc.
De par la place centrale du côté probabiliste, l'estimation de distribution partage de nombreux points communs avec les stratégies d'évolution, une des premières métaheuristique proposée, et les algorithmes de colonie de fourmis. Mais on peut également pointer les similarités avec le recuit simulé (qui utilise la fonction objectif comme distribution de probabilité pour construire un échantillon) et les algorithmes génétiques, dont les algorithmes à estimation de distribution sont issus, et dont ils utilisent toujours les opérateurs de sélection.
De la même façon, on trouve de nombreux points communs entre ces métaheuristiques d'optimisation et les outils de l'apprentissage automatique, comme les méthodes utilisant des arbres de décision ou des modèles de mélanges gaussiens. La différence est parfois difficile à préciser ; on peut en effet rencontrer des métaheuristiques effectuant des tâches d'apprentissage, des méthodes d'apprentissage résolvant des problèmes d'optimisation considérés comme difficiles (au sens de la théorie de la complexité), ou encore des outils d'apprentissage utilisés au sein de métaheuristiques.
Références
Sources
- (en) Pedro Larrañaga et José A. Lozano (éditeurs), Estimation of Distribution Algorithms: A New Tool for Evolutionary Computation (Genetic Algorithms and Evolutionary Computation), Éd. Kluwer Academic Publishers, 416 pages, 2001. (ISBN 0792374665).
- (fr) Johann Dréo, Alain Petrowski, Éric Taillard et Patrick Siarry, Métaheuristiques pour l'optimisation difficile, Éd. Eyrolles, Paris, , Broché, 356 pages, (ISBN 2-212-11368-4).
- Rechenberg, I., Cybernetic Solution Path of an Expeimental Problem, Royal Aircraft Establishment Library Translation, 1965
- Holland, John H., Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor, 1975
- M. Dorigo, Optimization, Learning and Natural Algorithms, Thèse de doctorat, Politecnico di Milano, Italie, 1992.
- S. Baluja. Population-based Incremental Learning : A Method for Integrating Genetic Search Based Function Optimization and Competitive Learning. Technical Report CMU-CS-94-163, Carnegie Mellon University, 1994
- Mühlenbein, H., Paaß, G., From recombination of genes to the estimation of distribution I. Binary parameters, Lectures Notes in Computer Science 1141: Parallel Problem Solving from Nature, tome PPSN IV, pages 178--187, 1996
Voir aussi
- (en) Jose A. Lozano, Pedro Larranaga, Inaki Inza et Endika Bengotxea (éditeurs), Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms, Éd. Springer-Verlag, 294 pages, 2006. (ISBN 3540290060)
- (en) Martin Pelikan, Kumara Sastry et Erick Cantú-Paz (éditeurs), Scalable Optimization via Probabilistic Modeling: From Algorithms to Applications, Éd. Springer, 350 pages, 2006. (ISBN 3540349537)


