Arbre de décision
Un arbre de décision est un outil d'aide à la décision représentant un ensemble de choix sous la forme graphique d'un arbre. Les différentes décisions possibles sont situées aux extrémités des branches (les « feuilles » de l'arbre), et sont atteintes en fonction de décisions prises à chaque étape. L'arbre de décision est un outil utilisé dans des domaines variés tels que la sécurité, la fouille de données, la médecine, etc. Il a l'avantage d'être lisible et rapide à exécuter. Il s'agit de plus d'une représentation calculable automatiquement par des algorithmes d'apprentissage supervisé.
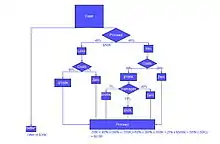
Présentation
Les arbres de décision sont utilisés dans des domaines d'aide à la décision (par exemple l'informatique décisionnelle) ou l'exploration de données. Ils décrivent comment répartir une population d'individus (clients d'une entreprise, utilisateurs d'un réseau social, …) en groupes homogènes selon un ensemble de variables discriminantes (âge, temps passé sur un site Web, catégorie socio-professionnelle, …) et en fonction d'un objectif fixé (aussi appelé « variable d'intérêt » ou « variable de sortie » ; par exemple : chiffre d'affaires, probabilité de cliquer sur une publicité, …). Par exemple, l'arbre de décision ci-dessous (tiré de l'ouvrage de Quilan[1]) illustre le cas où l'on cherche à prédire le comportement de sportifs (la variable à prédire Jouer prenant l'une des deux valeurs « oui » ou « non ») en fonction de données météorologiques (Ensoleillement, Température, Humidité ou Vent), appelées variables prédictives.
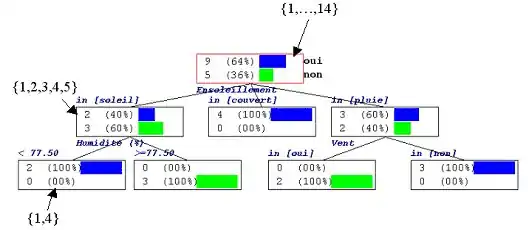
Chaque nœud de l’arbre décrit la distribution de la variable Jouer à prédire. Dans le cas du premier nœud, la racine de l’arbre, nous constatons qu’il y a 14 observations dans notre fichier : 9 cas où une partie a eu lieu (Jouer = oui) et 5 où aucune partie n'a eu lieu (Jouer = non). Ce premier nœud a plusieurs fils construits en utilisant la variable Ensoleillement : le plus à gauche (Ensoleillement = Soleil) comporte 5 observations, le suivant (Ensoleillement = couvert) en comporte 4, et ainsi de suite. La suite de décisions continue jusqu'à ce que, dans l'idéal, les observations dans un nœud soient toutes « oui » ou toutes « non ». On dit alors que le nœud est homogène.
Le processus de décision s'arrête aux feuilles de l’arbre. Dans l'arbre ci-dessus, toutes les feuilles sont homogènes, c'est-à-dire que les variables prédictives utilisées permettent de prédire complètement (sur ce fichier de données) si une partie va avoir lieu ou non. (Notons qu'il serait possible de construire l'arbre selon un ordre différent des variables de météo, par exemple en considérant l'humidité plutôt que l'ensoleillement à la première décision). L'arbre se lit intuitivement de haut en bas, ce qui se traduit en termes de règles logiques sans perte d’informations : par exemple, la feuille la plus à gauche se lit : « si ensoleillement = soleil et humidité < 77,5 % alors jouer = oui ».
Utilisation en apprentissage automatique
Un avantage majeur des arbres de décision est qu'ils peuvent être calculés automatiquement à partir de bases de données par des algorithmes d’apprentissage supervisé. Ces algorithmes sélectionnent automatiquement les variables discriminantes à partir de données non structurées et potentiellement volumineuses. Ils peuvent ainsi permettre d'extraire des règles logiques de cause à effet (des déterminismes) qui n'apparaissaient pas initialement dans les données brutes.
Extensions
Certains formalismes alternatifs proposent d'ajouter des règles de transition plus complexes dans chaque nœud. Ces formalismes sont alors utiles non pas pour l’apprentissage automatique mais pour la construction incrémentale de bases de connaissances, quand on dispose d'un expert dans le domaine d'application visé. On peut citer les Règles Dé-Roulées (Ripple Down Rules (en)), les EDAG (Exception directed acyclic graphs)[2], ou les nœuds de situation (nos) du logiciel libre EdiNoS.
Par ailleurs, un autre usage en apprentissage automatique consiste à construire non pas un arbre mais une forêt d'arbres de décision. Une décision est alors prise en faisant « voter » l'ensemble des arbres et en choisissant la réponse majoritaire (pour un choix discret) ou la moyenne des réponses (pour une variable continue).
Voir aussi
Articles connexes
Liens externes
- Une introduction aux arbres de décision
- EdiNoS, logiciel libre permettant de construire des graphes décisionnels étendus
Références
- R. Quinlan: C4.5: Programs for Machine Learning, Morgan Kaufmann Publishers Inc., 1993.
- (en) Brian Gaines, « Exceptions DAGS as Knowledge Structure », AAAI Technical Report WS-94-03, (lire en ligne)