Algèbre des parties d'un ensemble
En théorie des ensembles, l'ensemble des parties d'un ensemble, muni des opérations d'intersection, de réunion, et de passage au complémentaire, possède une structure d'algèbre de Boole. D'autres opérations s'en déduisent, comme la différence ensembliste et la différence symétrique.
L'algèbre des parties d'un ensemble étudie l'arithmétique de ces opérations (voir l'article « Opération ensembliste » pour des opérations qui ne laissent pas stable l'ensemble des parties d'un ensemble).
Inclusion et égalité
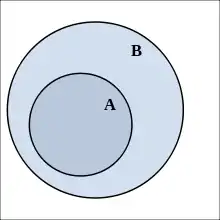
A ⊂ B (ou A ⊆ B).
Dans tout l'article, les ensembles considérés sont tous supposés inclus dans un ensemble donné U. L'inclusion est une relation d'ordre (partielle) notée « ⊂ » ou « ⊆ », et définie sur l'ensemble des parties de U, noté P(U), par :
- A ⊂ B si et seulement si ∀ x ∈ U (x ∈ A ⇒ x ∈ B).
L'égalité est définie par extensionnalité, deux ensembles sont égaux quand ils ont les mêmes éléments, c'est-à-dire que :
- A = B si et seulement si ∀ x ∈ U (x ∈ A ⇔ x ∈ B).
ou encore
- A = B si et seulement si A ⊂ B et B ⊂ A.
Les propriétés qui suivent correspondent donc, pour les égalités, à des équivalences en calcul propositionnel dont elles se déduisent. Elles peuvent être visualisées avec les diagrammes de Venn, une façon schématique de décrire toutes les cas possibles pour l'appartenance d'un élément à un nombre fini (et suffisamment réduit) d'ensembles, et qui peut donc permettre également de décrire des démonstrations d'égalité ou d'inclusion.
De façon similaire, les inclusions se ramènent à des implications.
Réunion et intersection
Réunion de deux ensembles
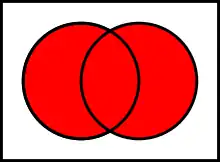
L'ensemble réunion de A et de B, noté « A U B » (lire « A union B »), est l'ensemble des éléments appartenant à A ou à B :
c'est-à-dire que :
- x ∈ A ∪ B si et seulement si x ∈ A ou x ∈ B.
Propriétés
L'ensemble U muni de la réunion a les propriétés suivantes (pour tous sous-ensembles A, B, C de U) :
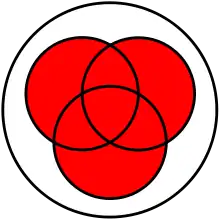
- (associativité) : le résultat de la réunion de plusieurs ensembles ne dépend pas de l'ordre dans lequel les opérations de réunion sont faites :
- et on note A ∪ B ∪ C cet ensemble ;
- (commutativité) : la réunion de deux ensembles ne dépend pas de l'ordre dans lequel ces deux ensembles sont pris :
- ;
- (idempotence) : la réunion d'un ensemble quelconque avec lui-même redonne cet ensemble :
- ;
- Ø est neutre : la réunion de l'ensemble vide avec un ensemble quelconque redonne cet ensemble :
- ;
- U est absorbant : U ∪ A = U.
L'ensemble A ∪ B est la borne supérieure pour l'inclusion des deux ensembles A et B, c'est-à-dire qu'il contient A et B, et qu'il est contenu dans tout ensemble contenant A et B :
- A ⊂ A ∪ B, B ⊂ A ∪ B et ∀ C [(A ⊂ C et B ⊂ C) ⇒ A ∪ B ⊂ C].
Par conséquent l'inclusion se définit à partir de la réunion :
- A ⊂ B si et seulement si A ∪ B = B.
Intersection de deux ensembles
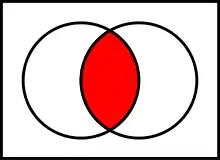
L'ensemble intersection de A et de B, noté « A ∩ B » (lire « A inter B ») est l'ensemble des éléments de A qui sont également éléments de B, soit :
c'est-à-dire que :
- x ∈ A ∩ B si et seulement si x ∈ A et x ∈ B.
Deux ensembles qui n'ont aucun élément en commun, c'est-à-dire que leur intersection est vide, sont dits disjoints.
Propriétés
Les propriétés de l'intersection sont similaires à celles de la réunion. On dit qu'elles sont duales de celles-ci, car on les obtient en remplaçant le signe de réunion par celui d'intersection, et si nécessaire en échangeant ∅ et U, l'inclusion et sa réciproque. Pour tous sous-ensembles A, B, C de U on a les propriétés suivantes :
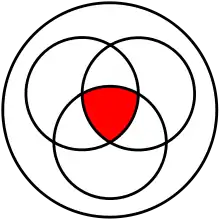
- (associativité) : le résultat de l'intersection de plusieurs ensembles ne dépend pas de l'ordre dans lequel les opérations sont faites :
- et on note A ∩ B ∩ C cet ensemble ;
- (commutativité) : l'intersection de deux ensembles ne dépend pas de l'ordre dans lequel ces deux ensembles sont pris
- ;
- (idempotence) : l'intersection d'un ensemble quelconque avec lui-même redonne cet ensemble
- (Ø absorbant) : l'intersection de l'ensemble vide et d'un ensemble quelconque est vide
- ;
- U est neutre : U ∩ A = A.
L'ensemble A ∩ B est la borne inférieure pour l'inclusion des deux ensembles A et B, c'est-à-dire qu'il est inclus dans A et dans B, et qu'il contient tout ensemble inclus à la fois dans A et dans B :
- A ∩ B ⊂ A, A ∩ B ⊂ B et ∀ C [(C ⊂ A et C ⊂ B) ⇒ C ⊂ A ∩ B].
Ceci permet de définir l'inclusion à partir de l'intersection cette fois :
- A ⊂ B si et seulement si A ∩ B = A.
Distributivité
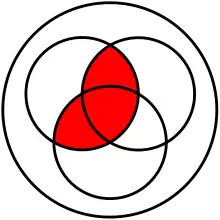
(A ∩ B) ∪ (A ∩ C).
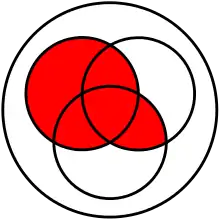
(A ∪ B) ∩ (A ∪ C).
Les deux opérations de réunion et d'intersection sont distributives l'une par rapport à l'autre, c'est-à-dire que l'on a les deux propriétés suivantes, pour tous ensembles A, B, C :
- (distributivité de l'intersection par rapport à la réunion : l'intersection de la réunion de deux ensembles avec un troisième ensemble est égale à la réunion de l'intersection de chacun des deux premiers ensembles avec le troisième :
- ;
- (distributivité de la réunion par rapport à l'intersection) : la réunion de l'intersection de deux ensembles avec un troisième ensemble est égale à l'intersection de la réunion de chacun des deux premiers ensembles avec le troisième :
- .
Réunion et intersection : cas général
Il est possible de généraliser la réunion à un nombre fini d'ensembles : on se ramène au cas de deux ensembles par réunion binaires successives et l'associativité de la réunion assure que l'ordre n'a pas d'importance. De même pour l'intersection.
Mais il est possible également de généraliser ces opérations à une famille non nécessairement finie d'ensembles.
La réunion d'une famille d'ensembles est définie par :
- .
Cette définition ne dépend pas de U. La réunion d'une famille vide est l'ensemble vide.
L'intersection d'une famille d'ensembles est définie par :
- .
La définition ci-dessus ne dépend pas de l'ensemble U sauf quand la famille est vide. dans ce dernier cas l'intersection de la famille vide est par définition l'ensemble de référence U, ce qui reste compatible avec les propriétés de l'intersection. On ne peut pas définir « dans l'absolu » (sans ensemble de référence) l'intersection d'une famille vide.
Certaines des propriétés de la réunion et de l'intersection binaire se généralisent au cas infini. Ce sont maintenant des propriétés du calcul des prédicats (et plus seulement du calcul propositionnel) qui sont en jeu. En particulier :
- l'intersection et la réunion d'une famille ne dépendent que de l'ensemble image de la famille, ce qui généralise l'associativité, la commutativité et l'idempotence, et découle directement de la définition ;
- l'intersection d'une famille d'ensemble (Ei)i ∈ I est la borne inférieure de l'ensemble {Ei | i ∈ I} ;
- la réunion d'une famille d'ensemble (Ei)i ∈ I est la borne supérieure de l'ensemble {Ei | i ∈ I} ;
- l'intersection binaire se distribue sur une réunion quelconque, de même que la réunion binaire sur une intersection quelconque :
- ; ;
- plus généralement, on a l'égalité (dans laquelle l'inclusion est immédiate mais l'inclusion utilise l'axiome du choix si est infini) ainsi que l'égalité duale[1].
Complémentaire


Un ensemble de référence U étant donné, le complémentaire du sous-ensemble A de U (sous-entendu relativement à U) est l'ensemble des éléments de U qui n'appartiennent pas à A. Il est noté U - A, A, Ac, ou encore :
c'est-à-dire que
- x ∈ A c si et seulement si x ∈ U et x ∉ A.
Le complémentaire de A dépend de l'ensemble de référence U. Il est également caractérisé par les deux égalités :
- A ∩ Ac = ∅ et A ∪ Ac = U.
L'opération de passage au complémentaire est involutive c'est-à-dire que (Ac)c = A.
Lois de De Morgan
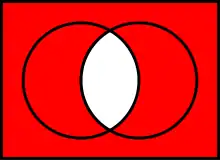
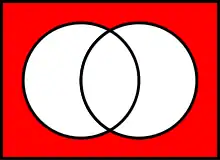
Le passage au complémentaire inverse la relation d'inclusion :
- A ⊂ B si et seulement si B c ⊂ Ac
et par conséquent il échange la réunion et l'intersection, qui sont la borne supérieure et la borne inférieure, ce sont les lois de De Morgan :
- (A ∩ B)c = Ac ∪ B c ;
- (A ∪ B)c = Ac ∩ B c.
Une structure ordonnée qui, comme l'ensemble des parties de U muni des opérations binaires de réunion et d'intersection, de l'opération de passage au complémentaire, et des deux éléments distingués ∅ et U, vérifie les propriétés de ces opérations énumérées jusqu'à présent est appelée algèbre de Boole.
Différence et différence symétrique
Différence
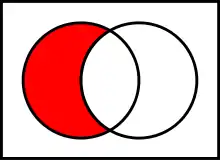
A \ B = A ∩ B c.
La différence ensembliste de A et B notée « A \ B » (lire « A moins B ») est l'ensemble des éléments de A qui n'appartiennent pas à B, soit :
- .
La différence de A et B dans U se définit à partir du complémentaire par A ∩ B c, et alors (A ∩ B c)c = A c ∪ B.
Si B est inclus dans A, alors A \ B se note aussi « A – B »[2] (lire encore « A moins B »), et s'appelle complémentaire de B dans A (ou relativement à A). On retrouve la notion de complémentaire ci-dessus, qui est le complémentaire relativement à U :
- .
Propriétés de la différence
On a :
- x ∈ A \ B si et seulement si x ∈ A et x ∉ B
- x ∉ A \ B si et seulement si x ∉ A ou x ∈ B
et donc :
- A \ B = ∅ si et seulement si A ⊂ B.
Les propriétés de la différence s'obtiennent à partir de sa définition et de celles de la réunion de l'intersection et du complémentaire. Par exemple la première qui suit est une suite d'intersections, alors que la seconde utilise une loi de De Morgan et la distributivité de l'intersection sur la réunion.
- .
Différence symétrique
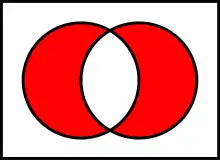
A Δ B = (A ∩ B c) ∪ (A c ∩ B).
La différence symétrique de A et de B, notée « A Δ B » (lire « A delta B ») est l'ensemble des éléments qui appartiennent soit à A, soit à B, mais pas aux deux à la fois. C'est la différence de A ∪ B et de A ∩ B. On peut l'écrire sous diverses formes :
- .
On a :
- x ∈ A Δ B si et seulement si ou bien x ∈ A ou bien x ∈ B (ou exclusif)
- x ∉ A Δ B si et seulement si x ∈ A ⇔ x ∈ B
ainsi la différence symétrique de deux ensembles est vide si et seulement si les deux ensembles sont égaux :
- A Δ B = ∅ si et seulement si A = B.
Propriétés de la différence symétrique
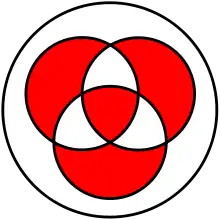
L'ensemble des parties de U muni de l'opération de différence symétrique est un groupe commutatif, avec ∅ pour élément neutre, et où chaque sous-ensemble de U est son propre opposé, c'est-à-dire que pour tous sous-ensembles A, B, C de U, on a :
- (associativité) : la différence symétrique de trois ensembles ne dépend pas de l'ordre dans lequel les opérations sont effectuées, le parenthésage n'est pas nécessaire :
- et on peut écrire A Δ B Δ C.
- (commutativité) : la différence symétrique de deux ensembles ne dépend pas de l'ordre dans lequel ces ensembles sont pris :
- Ø est élément neutre : la différence symétrique de l'ensemble vide et d'un autre ensemble redonne cet ensemble :
- Chaque sous-ensemble est son propre opposé : la différence symétrique de tout ensemble avec lui-même donne l'ensemble vide :
Une conséquence est la régularité : si A Δ B = A Δ C, alors B = C.
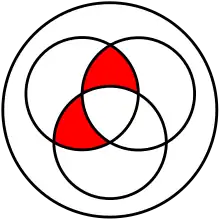
(A ∩ B) Δ (A ∩ C).
L'ensemble des parties de U muni, en plus de la différence symétrique, de l'intersection, est un anneau commutatif unitaire, c'est-à-dire qu'en plus des propriétés d'associativité et de commutativité de l'intersection, et de ce que U est élément neutre
- Distributivité de ∩ par rapport à Δ : l'intersection d'un ensemble avec la différence symétrique de deux autres ensembles est égale à la différence symétrique des intersections du premier ensemble avec chacun des deux autres :
- .
La différence symétrique, contrairement à la réunion, n'est pas distributive par rapport à l'intersection.
C'est une propriété générale des algèbres de Boole qu'une opération définie comme la différence symétrique (avec la réunion l'intersection et le passage au complémentaire) permet de définir une structure d'anneau, appelé parfois anneau de Boole. D'autres propriétés, communes à toutes les algèbres de Boole, sont vérifiées comme :
- Ac = U Δ A et donc Ac Δ A = U.
ou encore (A Δ B)c = A c Δ B = A Δ B c.
Aspects axiomatiques
D'un point de vue axiomatique, en théorie des ensembles tout ce qui précède se développe à partir de l'axiome d'extensionnalité (égalité de deux ensembles), qui garantit en particulier l'unicité des constructions introduites, et du schéma d'axiomes de compréhension, qui garantit leur existence, tous les ensembles introduits étant définis comme sous-ensemble d'un ensemble U donné.
Notes et références
- Cet article est partiellement ou en totalité issu de l'article intitulé « Opération ensembliste » (voir la liste des auteurs).
- (en) Robert L. Vaught, Set Theory : An Introduction, Birkhäuser, , 2e éd. (1re éd. 1985) (lire en ligne), p. 21.
- Mais cette notation pour la différence ensembliste peut prêter à confusion avec la différence algébrique. Par exemple : tandis que .



















![x\in [A\cap (B\cup C)]\Leftrightarrow x\in [(A\cap B)\cup (A\cap C)]~.](https://img.franco.wiki/i/5acbc8e336cfed92b360b722b65846d98e70cb81.svg)





















![{\displaystyle [0,1]\setminus [0,1]=\varnothing }](https://img.franco.wiki/i/06ecff08f43debf54e375ccd9e00c314af01daf3.svg)
![{\displaystyle \{x-y\mid x,y\in [0,1]\}=[-1,1]}](https://img.franco.wiki/i/11ecd807661f45d16feb059a79e5e32aad1c54a0.svg)