Aire d'un triangle
L'aire d'un triangle est, en géométrie euclidienne, une mesure de la surface plane déterminée par trois points et les segments joignant ces points. L'intérêt de l'aire d'un triangle provient du fait que tout polygone peut être scindé en triangles. Il existe plusieurs méthodes de calcul de cette aire, suivant ce qui est connu du triangle, la plus connue étant celle utilisant une hauteur h et la base b associée :
Une autre formule, dite formule de Héron, permet le calcul de l'aire connaissant les longueurs des trois côtés a, b et c d'un triangle et donc aussi leur demi-somme p :
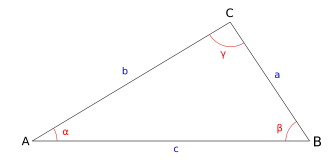
Elle peut se déduire de la loi des sinus, l'aire du triangle étant déduite d'un angle et de ses côtés adjacents. Si les deux côtés adjacents au sommet C d'un triangle ont pour longueur a et b et si l'angle en C a pour mesure γ, alors l'aire est donnée par :
Calcul de l'aire
À partir d'une hauteur
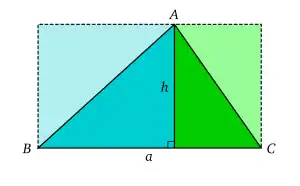
Si le triangle est rectangle, il est immédiat que son aire est
où a est la longueur d'un côté différent de l'hypoténuse et h la longueur de la hauteur issue de ce côté. Si le triangle n'est pas rectangle, la relation reste vraie, car le triangle se décompose en deux triangles rectangles (comme sur la figure).
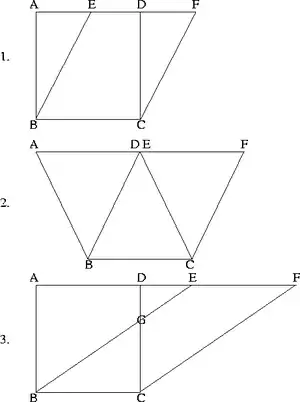
Démonstration par la méthode du cisaillement
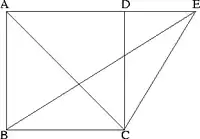
À partir de la formule donnant l'aire d'un rectangle, Euclide démontre d'une part (proposition XXXV du premier livre des Éléments) : « Les parallélogrammes constitués sur une même base, et entre mêmes parallèles, sont égaux[1] entre eux. » d'autre part (proposition XLI) : « Si un parallélogramme, et un triangle ont une même base, et sont entre mêmes parallèles ; le parallélogramme sera double du triangle. »
À partir des longueurs des trois côtés
Pour une expression de l'aire d'un triangle dont les longueurs des côtés sont a, b et c et le demi-périmètre , on peut utiliser la formule de Héron :
À partir des coordonnées des sommets
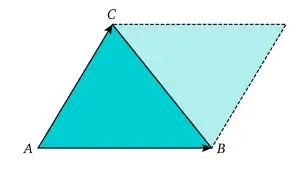
L'aire du parallélogramme défini par deux vecteurs , est la norme de leur produit vectoriel :
On peut calculer l'aire d'un triangle à partir de cette formule :
Un repère orthonormé étant donné, l'aire du triangle ABC peut être calculée à partir des coordonnées des sommets.
Dans le plan, si les coordonnées de A, B et C sont données par , et , alors l'aire S est la moitié de la valeur absolue du déterminant
L'aire du triangle ABC peut aussi se calculer à partir de la formule
Cette méthode se généralise en trois dimensions. L'aire du triangle ABC où , et s'exprime comme
Notes
- Cet article est partiellement ou en totalité issu de l'article intitulé « Théorème de Pythagore » (voir la liste des auteurs).
- Cet article est partiellement ou en totalité issu de l'article intitulé « Triangle » (voir la liste des auteurs).
- En langage actuel, on parlerait d’une égalité des aires plutôt que d’une égalité entre figures.
Voir aussi
Articles connexes
- Formulaire de géométrie classique
- Théorème de Routh
- S = rp : l'aire du triangle est le produit du rayon du cercle inscrit par le demi-périmètre.