Étude de fonction

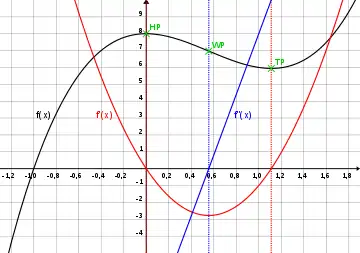
Lorsqu'une fonction est donnée par une représentation de courbe, la lecture graphique permet de lire son domaine de définition, à savoir l'ensemble des points de l'axe des abscisses (en général un intervalle ou une réunion d'intervalles) pour lesquels la courbe associe une ordonnée.

Les intersections de la courbe avec l'axe des abscisses indiquent les points d'annulation de la fonction, autrement dit les antécédents de 0. Si la fonction est continue, elle est de signe constant sur les intervalles du domaine de définition qui ne contiennent pas de point d'annulation (en dehors éventuellement de leurs extrémités). Il est possible alors de déterminer ce signe sur chacun de ces intervalles d'après la position relative de la courbe et de l'axe des abscisses :

• si la courbe est au-dessus de l'axe des abscisses, la fonction est positive sur cet intervalle ;
• si la courbe est en dessous de l'axe des abscisses, la fonction est négative sur cet intervalle.

La lecture graphique permet aussi de repérer les intervalles en abscisse sur lesquels la fonction est monotone, c'est-à-dire soit croissante, soit décroissante. Ces intervalles sont a priori différents des intervalles de signe constant.

Toutes ces informations peuvent être rassemblées dans un tableau de variations.

Lorsque la fonction ${\displaystyle f}$ est donnée par une expression, éventuellement définie par morceaux, son domaine de définition est déterminé par ceux des fonctions de référence utilisées et des domaines de validité des opérations en jeu.

Les zéros correspondent aux solutions de l'équation ${\displaystyle f(x)=0}$ et le signe est décrit par l'ensemble des solutions de l'une ou l'autre inéquation :

${\displaystyle f(x)\geq 0\qquad \mathrm {ou} \qquad f(x)\leq 0\ .}$

${\displaystyle x\mapsto \mathrm {e} ^{x}-x}$

Fonction définie sur l'ensemble des réels comme
différence de fonctions strictement croissantes.
Les méthodes de décomposition en fonctions de référence
ne permettent pas d'obtenir les variations de la fonction.

Dans certains cas simples, les variations de la fonction peuvent être obtenues à l'aide d'un tableau de décomposition de la fonction en fonctions de référence, mais cette méthode ne peut aboutir dès lors qu'intervient une opération pour laquelle les variations du résultat ne peuvent être déduites des variations des opérandes.

Si la fonction est dérivable, le calcul de la dérivée et l'étude du signe de celle-ci permettent en général de déterminer plus efficacement les variations de la fonction.

L'étude de fonction peut se poursuivre avec la détermination des limites aux bornes du domaine de définition, puis par la recherche d'asymptotes à la courbe.

Lorsque la fonction est définie comme solution d'une équation différentielle, les informations qui peuvent être obtenues dépendent de la complexité de l'équation.