Équation de Darcy-Weisbach

L’équation de Darcy pour les pertes de charge est une amélioration de l’équation de Prony (pour l'effet des parois) et un développement de l'équation de Borda–Carnot (pour l'effet des changements de section). Elle a été développée par Henry Darcy, avant d'être modifiée par Julius Weisbach (scientifique allemand) en 1845, qui lui donna sa forme actuelle.

La perte de pression s'exprime par :

${\displaystyle \Delta P=f_{D}\,{\frac {L}{D_{h}}}\,\rho {\frac {V^{2}}{2}}}$

La perte de charge, obtenue en divisant l'expression précédente par ρ·g s'exprime par :

${\displaystyle \Delta H=f_{D}\,{\frac {L}{D_{h}}}\,{\frac {V^{2}}{2g}}}$

avec

• ΔP - perte de pression [Pa]
• ΔH - perte de charge [m]
• f_D - coefficient de perte de charge de Darcy [-]
• L - longueur de la conduite [m]
• ρ - masse volumique du fluide [kg m⁻³]
• D_h - diamètre hydraulique [m]
• V - vitesse moyenne du fluide [m s⁻¹]
• g - accélération de la pesanteur [m s⁻²]

Les Anglo-Saxons désignent ces deux définitions par les termes pressure drop et head loss.

Diagramme de Moody

Le coefficient de perte de charge, dépend du régime d’écoulement (laminaire ou turbulent) et des propriétés du fluide. En conditions isothermes, le nombre de Reynolds, qui est le rapport entre la puissance des forces d'inertie et la dissipation visqueuse, suffit à caractériser le régime d'écoulement.

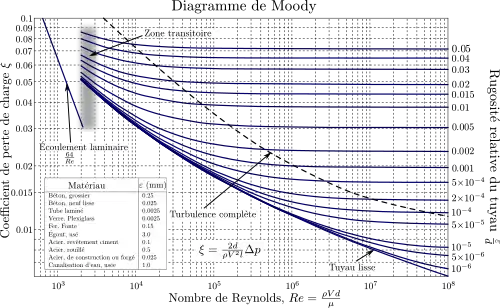
Plusieurs méthodes permettent de définir le coefficient de perte de charge. L'une des plus connues recourt au diagramme de Moody, qui est un abaque permettant de déterminer le coefficient de perte de charge à partir du nombre de Reynolds et de la rugosité (${\displaystyle \varepsilon }$) de la conduite. Il est également possible de calculer directement ce paramètre à partir de corrélations qui sont à la base du diagramme du Moody :

• pour un écoulement laminaire dans un tube circulaire, ${\displaystyle Re<2000}$[1], on obtient l'expression de ${\displaystyle f_{D}}$ par identification avec la loi de Hagen-Poiseuille :

${\displaystyle f_{D}={\frac {64}{Re}}}$ (soit pour le coefficient de Fanning :${\displaystyle f_{F}={\frac {16}{Re}}}$). Il est possible d'adapter cette formule selon la forme du tuyau[2].

• pour un écoulement turbulent dans un tube circulaire, ${\displaystyle Re>3000}$[1], il existe un grand nombre de corrélations, certaines simples mais imprécises, d’autres plus lourdes mais plus proches de la réalité.

Rugosité pour quelques types de matériaux[3]

Matériau	Rugosité (${\displaystyle \varepsilon }$) [mm]
fer forgé	0,12 - 0,3
conduite rivée	0,75 - 1-05
galvanisé	0,15 - 0,3
béton (petit tuyau)	0,15 - 0,25
béton rugueux	0,9 - 1,5
béton très rugueux	1,5 - 2,15
galerie rocheuse	90 - 300

Corrélation de Blasius[4], la plus simple, mais sa validité se réduit aux conduites parfaitement lisses (verre, PVC,...) :

${\displaystyle f_{D}=0,3164\,Re^{-{\frac {1}{4}}}}$

Corrélation de Colebrook, également connue sous le nom d'équation de Colebrook-White :

${\displaystyle {\frac {1}{\sqrt {f_{D}}}}=-2\log _{10}\left({\frac {2,51}{Re{\sqrt {f_{D}}}}}+{\frac {\varepsilon }{3,7D}}\right)}$

Corrélation de Haaland[5] :

${\displaystyle {\frac {1}{\sqrt {f_{D}}}}=-1,8\log _{10}\left({\frac {6,9}{Re}}+\left({\frac {\varepsilon }{3,7D}}\right)^{1,11}\right)}$

Corrélation de Swamee–Jain[6]:

${\displaystyle f_{D}={\frac {0,25}{\left(\log _{10}\left[{\frac {\varepsilon /D}{3,7}}+{\frac {5,74}{Re^{0,9}}}\right]\right)^{2}}}}$

Corrélation de Serghides[7]. La comparaison a été effectuée avec 70 points sur un large intervalle de valeurs tant pour le nombre de Reynolds que pour la rugosité avec une erreur absolue maximale de 0,0031 %.

${\displaystyle A=-2\log _{10}\left({\varepsilon /D \over 3,7}+{12 \over {\mbox{Re}}}\right)}$

${\displaystyle B=-2\log _{10}\left({\varepsilon /D \over 3,7}+{2,51A \over {\mbox{Re}}}\right)}$

${\displaystyle C=-2\log _{10}\left({\varepsilon /D \over 3,7}+{2,51B \over {\mbox{Re}}}\right)}$

${\displaystyle f_{D}=\left(A-{\frac {(B-A)^{2}}{C-2B+A}}\right)^{-2}}$

Corrélation de Goudar-Sonnad[8] - [9], montrant une erreur absolue maximale inférieure à 0,000 364 % sur plus de 10 000 points, pour des nombres de Reynolds ${\displaystyle \mathrm {Re} \in [4000,10^{8}]}$ et des rugosités relatives ${\displaystyle {\frac {\varepsilon }{D}}\in [10^{-6},10^{-2}]}$.

${\displaystyle a={2 \over \ln(10)}}$ ; ${\displaystyle b={\varepsilon /D \over 3,7}}$ ; ${\displaystyle d={\ln(10)Re \over 5,02}}$

${\displaystyle s=bd+\ln(d)}$ ; ${\displaystyle q=s^{\frac {s}{(s+1)}}}$

${\displaystyle g={bd+\ln {d \over q}}}$ ; ${\displaystyle z={\ln {q \over g}}}$

Deux possibilités différentes sont disponibles pour calculer δ

1) ${\displaystyle \delta _{LA}=z{g \over {g+1}}}$

2) ${\displaystyle \delta _{CFA}=\delta _{LA}\left((1+{\frac {z/2}{(g+1)^{2}+(z/3)(2g-1)}})\right)}$

${\displaystyle {\frac {1}{\sqrt {f_{D}}}}=a\left[\ln {\left({\frac {d}{q}}\right)}+\delta \right]}$

• Stuart W. Churchill[10] a développé une formule pour les deux régimes, laminaire et turbulent :

${\displaystyle f_{D}=8\left(\left({\frac {8}{Re}}\right)^{12}+\left(A+B\right)^{-1,5}\right)^{\frac {1}{12}}}$

${\displaystyle A=\left(2{,}457\ln \left(\left(\left({\frac {7}{Re}}\right)^{0,9}+0,27{\frac {\varepsilon }{D}}\right)^{-1}\right)\right)^{16}}$

${\displaystyle B=\left({\frac {37530}{Re}}\right)^{16}}$

En régime turbulent, certains auteurs précisent le champ d'application des formules précédentes, en fonction du produit ${\displaystyle {\mbox{Re}}\,{\frac {\varepsilon }{D}}}$, caractérisant la rugosité des conduites[11] :

• Pour ${\displaystyle {\mbox{Re}}\,{\frac {\varepsilon }{D}}<65}$ (conduite lisse) :
  • pour ${\displaystyle 2300<{\mbox{Re}}<10^{5}}$ : formule de Blasius indiquée ci-dessus ;
  • pour ${\displaystyle 2300<{\mbox{Re}}<10^{6}}$ : formule de Hermann : ${\displaystyle f_{D}=0{,}0054+{\frac {0{,}396}{{\mbox{Re}}^{0,3}}}}$ ;
  • pour ${\displaystyle 10^{5}<{\mbox{Re}}<5\,10^{6}}$ : formule de Nikuradzé[11] : ${\displaystyle f_{D}=0{,}0032+0{,}221\,{\mbox{Re}}^{-0{,}237}}$ ;
  • pour ${\displaystyle {\mbox{Re}}>10^{6}}$ : formule de Prandtl et v. Kármán[11] : ${\displaystyle {\frac {1}{\sqrt {f_{D}}}}=2\,log_{10}\left({{\mbox{Re}}\,{\sqrt {f_{D}}}}\right)-0{,}8}$.

• Pour ${\displaystyle {\mbox{Re}}\,{\frac {\varepsilon }{D}}>1300}$ (conduite rugueuse) :
  • formule de Nikuradzé[11] : ${\displaystyle {\frac {1}{\sqrt {f_{D}}}}=2\,\log _{10}\left({\frac {D}{\varepsilon }}\right)+1{,}14}$
  • formule de Moody[11] : ${\displaystyle f_{D}=0{,}0055+0{,}15\,\left({\frac {\varepsilon }{D}}\right)^{\frac {1}{3}}}$
  • formule de Eck[11] : ${\displaystyle f_{D}={\frac {0{,}25}{\left(log_{10}\left(3{,}71\,{\frac {D}{\varepsilon }}\right)\right)^{2}}}}$

• Pour ${\displaystyle 65<{\mbox{Re}}\,{\frac {\varepsilon }{D}}<1300}$ (conduite intermédiaire) :
  • formule de Prandlt et Colebrook indiquée ci-dessus (formule de Colebrook)
  • formule de Altschoul[11] : ${\displaystyle {\frac {1}{\sqrt {f_{D}}}}=1{,}8\,\log _{10}\left({\frac {\mbox{Re}}{{\mbox{Re}}\,\left({\frac {\varepsilon }{10\,D}}\right)+7}}\right)}$
  • formule de Citrini[11] : ${\displaystyle f_{D}={\frac {1+{\frac {8}{{\mbox{Re}}\,{\frac {\varepsilon }{D}}}}}{\left(2\,\log _{10}\left(3{,}71\cdot {\frac {D}{\varepsilon }}\right)\right)^{2}}}}$

• Application Web avec des calculs de perte de charge pour tuyaux et conduits