Triangle cévien

Dans un triangle ABC, on considère un point P, non situé sur les côtés du triangle. Les droites (PA) et (BC) se croisent en P_A, les droites (PB) et (AC) se croisent en P_B, et les droites (PC) et (AB) se croisent en P_C. Alors le triangle P_AP_BP_C est appelé triangle cévien de P pour le triangle ABC. Le cercle circonscrit au triangle cévien de P est le cercle cévien.

Il ne doit pas être confondu avec le triangle pédal, qui est le triangle formé par les projections orthogonales du point P sur les côtés.

• le triangle cévien de l'orthocentre est le triangle orthique
• le triangle cévien du centre de gravité est le triangle médian
• le triangle cévien du point de Gergonne est le triangle de contact (points où le cercle inscrit touche les côtés du triangle)

• Les points P_A,P_B,P_C, vérifient la relation de Ceva : ${\displaystyle {\frac {\overline {P_{A}B}}{\overline {P_{A}C}}}{\frac {\overline {P_{B}C}}{\overline {P_{B}A}}}{\frac {\overline {P_{C}A}}{\overline {P_{C}B}}}=-1}$.
• Le point P a pour coordonnées barycentriques dans ${\displaystyle (A,B,C)}$ : ${\displaystyle \left(-{\frac {\overline {P_{B}C}}{\overline {P_{B}A}}}:-{\frac {\overline {P_{A}C}}{\overline {P_{A}B}}}:1\right)}$.
• Un triangle et le triangle cévien du point P pour ce triangle sont en homologie par rapport à P. Par le théorème de Desargues, il existe également une droite (l'axe de l'homologie) par rapport à laquelle les deux triangles sont en homologie ; par exemple, dans le cas où P est à l'orthocentre, il s'agit de l'axe orthique[1].

• L'aire du triangle cévien du point P de coordonnées trilinéaires (α : β : γ) est donnée par :

${\displaystyle {\mathcal {A}}_{cevian}={\frac {2abc|\alpha \beta \gamma |}{\left|(\alpha a+\beta b)(\beta b+\gamma c)(\gamma c+\alpha a)\right|}}{\mathcal {A}}_{ABC}}$

• Les symétriques des sommets d'un triangle cévien par rapport aux milieux des côtés forment un autre triangle cévien : si on trace P_A', le symétrique de P_A par rapport au milieu de BC, et qu'on construit de même P_B' et P_C', alors il existe un point P' tel que P_A'P_B'P_C' soit le triangle cévien de P' pour le triangle ABC[2].

Le point P' est alors appelé conjugué isotomique de P.

• Le cercle cévien d'un point P intersecte AB en P_C et P_C", BC en P_A et P_A", et AC en P_B et P_B". Alors il existe P" tel que P_A"P_B"P_B" soit le triangle cévien de P" pour le triangle ABC[2].

Le point P" est alors appelé conjugué cyclocévien de P.

• 
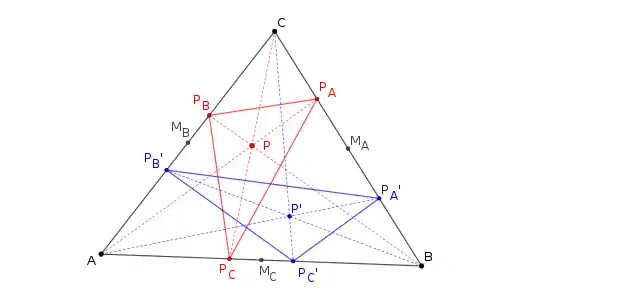  Les symétriques des sommets d'un triangle cévien dans un triangle par rapport aux milieux des côtés forment un autre triangle cévien (en bleu).
• 
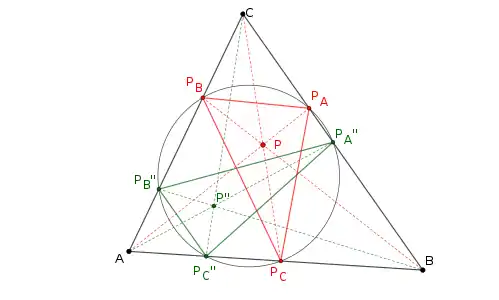  Le cercle circonscrit d'un triangle cévien à un triangle forme un autre triangle cévien dans le même triangle (en vert).

• Droite centrale

(en) Eric W. Weisstein, « Cevian Triangle », sur MathWorld