Cévienne

En géométrie, une cévienne d'un triangle est, dans son acception la plus générale, une droite passant par l'un des sommets [1] - [2]. Certains auteurs restreignent la définition au cas d'un segment joignant un sommet à son côté opposé, voire utilisent les deux définitions [3].

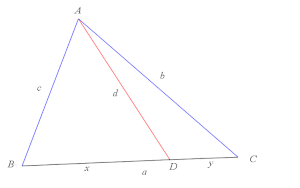
Un triangle ABC, avec une cévienne issue de A.

Le mot cévienne vient du nom du mathématicien italien Giovanni Ceva, qui a prouvé un théorème portant son nom donnant une condition pour que trois céviennes passant chacune par un sommet du triangle soient concourantes ou parallèles.

Exemples

Les hauteurs, médianes, bissectrices, symédianes, les droites reliant les sommets aux points de contact du cercle inscrit, sont des céviennes particulières, toutes concourantes.

Définitions associées

Le pied d'une cévienne est le point d'intersection de la cévienne avec le côté opposé au sommet.

Le triangle cévien est le triangle formé par les trois pieds de trois céviennes passant chacune par un sommet du triangle, et le cercle cévien est le cercle circonscrit à ce triangle.

Longueur

Le théorème de Stewart permet de calculer la longueur d'une cévienne (segment) connaissant les longueurs des segments découpés par celle-ci sur le côté opposé.

Bibliographie

(en) Ross Honsberger (de), Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, Cambridge University Press, 1995 (ISBN 978-0-88385639-0), p. 13 et 137.
(en) Vladimir Karapetoff (en), Some properties of correlative vertex lines in a plane triangle, American Mathematical Monthly, 36 (1929), 476–9 jstor.

Notes et références

Alain Bouvier, Michel George, François Le Lionnais, Dictionnaire des mathématiques, PUF, 2005, p. 138
« Cévienne », sur Wiktionnaire
Mohammed AASSILA, 1000 challenges mathématiques, géométrie, Ellipses, 2018, p. 67, 468

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cevian » (voir la liste des auteurs).