Théorème des milieux
En géométrie élémentaire, le théorème des milieux, ou théorème de la droite des milieux, est un cas particulier du théorème de Thalès joint à sa réciproque.
Théorème direct
Énoncé
Si un segment joint les milieux de deux côtés d’un triangle, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de celle de ce troisième côté[1].
Formulation graphique
Le théorème peut être représenté graphiquement de la façon ci-dessous :
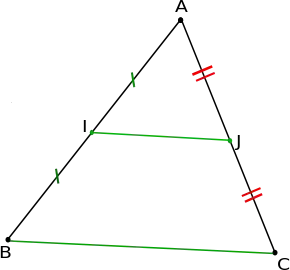
Démonstration en géométrie élémentaire
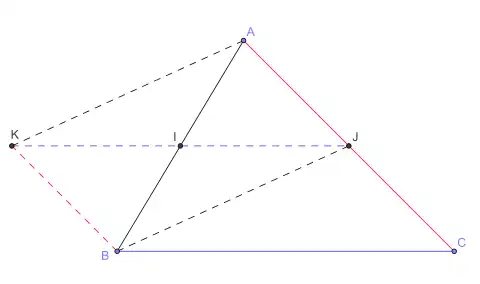
Cette propriété se démontre[2] sans que soit connue la définition d'un vecteur. Sur la figure, (IJ) est la droite des milieux dans ABC qu’on veut prouver parallèle à (BC).
Soit K le symétrique de J par rapport à I, on a alors I milieu de [JK] et IJ = KJ/2.
Comme I est par hypothèse le milieu de [AB], les diagonales de AJBK se coupent en leur milieu commun I, donc AJBK est un parallélogramme.
Ses côtés [AJ] et [KB] sont parallèles et de même longueur, et il en est donc de même pour [JC] et [KB].
KBCJ n’est pas croisé (B et C sont dans le même demi-plan par rapport à (KJ), B comme symétrique de A par rapport à I, C comme symétrique de A par rapport à J).
- Or si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur alors c'est un parallélogramme.
Donc KBCJ est un parallélogramme.
Par les propriétés du parallélogramme, les côtés opposés [KJ] et [BC] sont parallèles, la droite (IJ) est donc parallèle à (BC).
Comme les côtés opposés sont égaux, de KJ = BC on déduit : IJ = BC/2.
Démonstration vectorielle
Lorsque la notion de vecteur est déjà connue — par exemple, dans le cas d'un espace affine euclidien associé à un espace vectoriel — il existe une démonstration vectorielle beaucoup plus courte.
Puisque I est milieu de (A,B) et J est milieu de (A,C), on a
- , d'où
- .
Les vecteurs et sont colinéaires donc les droites (IJ) et (BC) sont parallèles.
La norme de est égale à la moitié de celle de , autrement dit la distance IJ est égale à BC/2.
On peut dissimuler la relation de Chasles utilisée ci-dessus, en assimilant l'espace affine à son espace vectoriel associé via le choix de A comme origine[3]. Les équations précédentes s'écrivent alors : B = 2I et C = 2J, d'où C – B = 2(J – I).
Théorème réciproque
C'est un cas particulier du Théorème de Thalès[4].
Théorème — Si une droite passe par le milieu d'un des côtés d'un triangle et si elle est parallèle à un autre côté alors elle coupe le troisième côté en son milieu[1].
Il existe une démonstration de cette réciproque faisant intervenir uniquement des notions d'aire.
- On suppose que la droite passe par le milieu I de côté [AB], qu'elle est parallèle au côté [BC] et qu'elle coupe le côté [AC] en un point J'.
- Le triangle CBI a même sommet que le triangle CBA et a une base moitié donc
- aire (CBI) = 1⁄2 aire (CBA).
- Le segment [IJ'] est parallèle à la base [BC] donc, par cisaillement,
- aire (CBI) = aire (CBJ').
- L'aire du triangle BCJ' est donc la moitié de l'aire du triangle BCA et les points C, J' et A sont alignés donc
- CJ' = 1⁄2 CA.
- Le point J' est donc égal au milieu J du segment [CA].
Alternativement, le théorème réciproque peut se démontrer élémentairement comme le théorème direct : en notant K' le symétrique de J' par rapport à I, le quadrilatère AJ'BK' est un parallélogramme donc (BK') est parallèle à (J'A) = (CJ'), si bien que BK'J'C est aussi un parallélogramme ; par conséquent, CJ' = BK' = J'A.
Remarquons que le théorème réciproque peut se déduire de la première affirmation du théorème direct[2], et inversement : avec les mêmes notations que ci-dessus, J est égal à J' si et seulement si (IJ) est parallèle à (IJ'), c'est-à-dire à (BC).
Notes et références
- Voir par exemple Françoise Mollet-Petit (dir.), Mathématiques 4e, Paris, Casteilla, coll. « IREM-Strasbourg », , chap. 4, p. 65, mais tout autre livre de mathématiques de 4e conforme au programme de 1988 ou encore de 2008 (voir « Bulletin officiel spécial no 6 du 28 août 2008 », p. 30) peut convenir.
- Voir par exemple Mollet-Petit 1988, p. 68.
- Cette démarche apparaît dans un exercice résolu de François Liret et Dominique Martinais, Mathématiques pour le DEUG : algèbre 1re année, Dunod, (ISBN 9782100031498, OCLC 41129019), p. 170.
- BO 2008, p. 30.



