Système de Johnson

Système de Johnson
Paramètres	${\displaystyle \gamma ,\xi ,\delta >0,\lambda >0}$ (réel)
Support	${\displaystyle ]\xi ,\xi +\lambda [}$
Densité de probabilité	${\displaystyle {\tfrac {\delta \lambda }{{\sqrt {2\pi }}(x-\xi )(\xi +\lambda -x)}}\exp \left[-{\tfrac {1}{2}}\left(\gamma +\delta \ln \left({\tfrac {x-\xi }{\lambda +\xi -x}}\right)\right)^{2}\right]}$
Fonction de répartition	${\displaystyle \Phi \left(\gamma +\delta \ln \left({\tfrac {x-\xi }{\lambda +\xi -x}}\right)\right)}$
Médiane	${\displaystyle {\frac {\xi +\exp \left(-{\tfrac {\gamma }{\delta }}\right)(\lambda +\xi )}{1+\exp \left(-{\tfrac {\gamma }{\delta }}\right)}}}$

N. L. Johnson a d'abord proposé la transformation[1]:

${\displaystyle z=\gamma +\delta \ln \left({\frac {\frac {x-\xi }{\lambda }}{1-{\frac {x-\xi }{\lambda }}}}\right)}$

où ${\displaystyle z\sim {\mathcal {N}}(0,1)}$.

La loi S_B de Johnson peut être générée à partir d'une variable aléatoire suivant une loi uniforme continue U par :

${\displaystyle y=\xi +{\frac {\lambda }{1+{\rm {e}}^{-\left(z-\gamma \right)/\delta }}}.}$

On reconnait la forme d'une fonction logistique.

Johnson a étendu la loi S_B en une version bivariée, notée S_BB. La densité de la loi est

${\displaystyle f(z_{1},z_{2},\rho )={\frac {1}{2\pi {\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2}}{\frac {z_{1}^{2}-2z_{1}z_{2}+z_{2}^{2}}{1-\rho ^{2}}}\right).}$

où z₁ et z₂ suivent chacun une loi S_B, et ${\textstyle \rho =\mathbb {E} (Z_{1}Z_{2})}$ la mesure de dépendance entre les deux variables[4].

Système de Johnson
Paramètres	${\displaystyle \gamma ,\xi ,\delta >0,\lambda >0}$ (réel)
Support	${\displaystyle ]\xi ,+\infty [}$
Densité de probabilité	${\displaystyle {\tfrac {\delta \lambda }{{\sqrt {2\pi }}(x-\xi )}}\exp \left[-{\tfrac {1}{2}}\left(\gamma +\delta \ln \left({\tfrac {x-\xi }{\lambda }}\right)\right)^{2}\right]}$
Fonction de répartition	${\displaystyle \Phi \left(\gamma +\delta \ln \left({\frac {x-\xi }{\lambda }}\right)\right)}$
Espérance	${\displaystyle \xi +\exp \left({\tfrac {1-2\gamma \delta }{2\delta ^{2}}}\right)}$
Médiane	${\displaystyle \xi +\lambda \exp \left(-{\frac {\gamma }{\delta }}\right)}$
Variance	${\displaystyle \exp \left({\tfrac {2(1-\gamma \delta )}{\delta ^{2}}}\right)}$
Asymétrie	${\displaystyle \exp \left({\tfrac {3(3-\gamma \delta )}{\delta ^{2}}}\right)}$

N. L. Johnson a d'abord proposé la transformation[1]:

${\displaystyle z=\gamma +\delta \ln \left({\frac {x-\xi }{\lambda }}\right)}$

où ${\displaystyle z\sim {\mathcal {N}}(0,1)}$.

La loi S_L de Johnson peut être générée à partir d'une variable aléatoire suivant une loi uniforme continue U par :

${\displaystyle y=\lambda {\rm {e}}^{-\left(z-\gamma \right)/\delta }+\xi .}$

La loi S_B convient pour modéliser les lois platikurtiques.

Système de Johnson
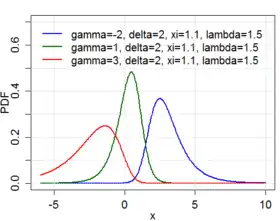Densité de probabilité
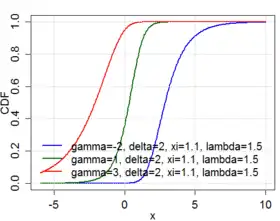Fonction de répartition
Paramètres	${\displaystyle \gamma ,\xi ,\delta >0,\lambda >0}$ (réel)
Support	${\displaystyle -\infty {\text{ vers }}+\infty }$
Densité de probabilité	${\displaystyle {\frac {\delta }{\lambda {\sqrt {2\pi }}{\sqrt {1+\left({\tfrac {x-\xi }{\lambda }}\right)^{2}}}}}\exp \left(-{\tfrac {1}{2}}\left(\gamma +\delta \operatorname {arsinh} \left({\tfrac {x-\xi }{\lambda }}\right)\right)^{2}\right)}$
Fonction de répartition	${\displaystyle \Phi \left(\gamma +\delta \operatorname {arsinh} \left({\frac {x-\xi }{\lambda }}\right)\right)}$
Espérance	${\displaystyle \xi -\lambda \exp \left({\tfrac {1}{2\delta ^{2}}}\right)\sinh \left({\frac {\gamma }{\delta }}\right)}$
Médiane	${\displaystyle \xi +\lambda \sinh \left(-{\frac {\gamma }{\delta }}\right)}$
Variance	${\displaystyle \mathrm {Var} (X)={\frac {\lambda ^{2}}{2}}\left[\exp \left({\tfrac {1}{\delta ^{2}}}\right)-1\right]\left(\exp \left({\tfrac {1}{\delta ^{2}}}\right)\cosh \left({\tfrac {2\gamma }{\delta }}\right)+1\right)}$
Asymétrie	${\displaystyle -{\frac {\lambda ^{3}\exp({\tfrac {1}{2\delta ^{2}}})\left(\exp({\tfrac {1}{\delta ^{2}}})-1\right)^{2}\left[\exp({\tfrac {1}{\delta ^{2}}})\left(\exp({\tfrac {1}{\delta ^{2}}})+2\right)\sinh({\tfrac {3\gamma }{\delta }})+3\sinh({\tfrac {2\gamma }{\delta }})\right]}{4\mathrm {Var} (X)^{3/2}}}}$
Kurtosis normalisé	${\displaystyle {\frac {\lambda ^{4}\left(\exp \left({\tfrac {1}{\delta ^{2}}}\right)-1\right)^{2}(K_{1}+K_{2}+K_{3})}{8\mathrm {Var} (X)^{2}}}}$ ${\displaystyle K_{1}=\exp \left({\tfrac {2}{\delta ^{2}}}\right)\left[\exp \left({\tfrac {4}{\delta ^{2}}}\right)+2\exp \left({\tfrac {3}{\delta ^{2}}}\right)+3\exp \left({\tfrac {2}{\delta ^{2}}}\right)-3\right]\cosh \left({\tfrac {4\gamma }{\delta }}\right)}$ ${\displaystyle K_{2}=4\exp \left({\tfrac {2}{\delta ^{2}}}\right)\left(\exp \left({\tfrac {1}{\delta ^{2}}}\right)+2\right)\cosh \left({\tfrac {3\gamma }{\delta }}\right)}$ ${\displaystyle K_{3}=3\left(2\exp \left({\tfrac {1}{\delta ^{2}}}\right)+1\right)}$

Les lois S_U de Johnson se basent sur la transformation de la loi normale suivante[1]:

${\displaystyle z=\gamma +\delta \operatorname {arsinh} \left({\frac {x-\xi }{\lambda }}\right)}$

où ${\displaystyle z\sim {\mathcal {N}}(0,1)}$.

La loi S_U de Johnson peut être générée à partir d'une variable aléatoire suivant une loi uniforme continue U par :

${\displaystyle y=\lambda \sinh \left(\left(z-\gamma \right)/\delta \right)+\xi .}$

Afin d'identifier le type de lois de Johnson à partir du tirage, il y a plusieurs méthodes, la plus simple étant la méthode des moments qui se base surtout sur les moments d'ordre 3 et 4. Par exemple, pour une loi S_L, ces moments valent[5]:

${\displaystyle \beta _{1}={\frac {\mu _{3}^{2}}{\mu _{2}^{3}}}=({\rm {e}}^{\delta ^{-2}}-1)({\rm {e}}^{\delta ^{-2}}+2)^{2},\beta _{2}={\frac {\mu _{4}}{\mu _{2}^{2}}}={\rm {e}}^{4\delta ^{-2}}+2{\rm {e}}^{3\delta ^{-2}}+3{\rm {e}}^{2\delta ^{-2}}-3.}$

Ainsi, toute loi de Johnson vérifie ${\displaystyle \beta _{2}-\beta _{1}-1\geqslant 0}$.

D'autres moyens ont été développés, reposant sur la méthode d'adaptation des quantiles, la méthode des moindres carrés, ou des estimateurs statistiques[3] - [6] - [7].