Superéchange

Le superéchange (ou le superéchange de Kramers et Anderson) est le couplage antiferromagnétique fort (normalement) entre deux cations qui sont deuxièmes voisins à travers un anion non-magnétique. Il diffère ainsi de l'échange direct pour lequel il y a couplage entre des cations qui sont voisins immédiats sans impliquer un anion intermédiaire. Le superéchange est la conséquence du fait que les électrons proviennent du même atome donneur et sont couplés avec les spins des ions accepteurs. Si les deux cations qui sont deuxièmes voisins sont liés à 90 degrés à l'anion pont non-magnétique, alors l'interaction peut être une interaction ferromagnétique.

Fig. 1 : superéchange pour le MnO

Le superéchange est proposé par Hendrik Kramers en 1934 lorsqu'il remarque que dans des cristaux tels que ceux d'oxyde de manganèse(II) (MnO), il y a une interaction entre des atomes de Mn malgré la présence des atomes non-magnétiques d'oxygène entre eux[1]. Puis Philip Anderson améliore le modèle de Kramers en 1950[2].

Les propriétés magnétiques d'une gamme large de matériaux sont interprétées de façon qualitative avec grand succès à l'aide d'un ensemble de règles semi-empiriques développées par John B. Goodenough et Junjiro Kanamori dans les années 1950[3] - [4] - [5]. Ces règles de Goodenough-Kanamori sont basées sur les relations de symétrie et les nombres d'électrons qui occupent les orbitales atomiques en recouvrement, en supposant que les liaisons chimiques sont mieux décrites par le modèle localisé de la théorie de la liaison de valence que par le modèle délocalisé de la théorie des bandes. En conséquence du principe d'exclusion de Pauli, le superéchange entre deux ions magnétiques avec orbitales demi-occupées qui sont couplés à travers un ion non-magnétique intermédiaire (par exemple O²⁻) sera fortement antiferromagnétique, tandis que le couplage entre un ion avec une orbitale remplie et un ion avec une orbitale demi-remplie sera ferromagnétique. Quant au couplage entre un ion avec une orbitale vide et une orbitale demi-remplie ou bien remplie, il peut être soit antiferromagnétique soit ferromagnétique, mais le cas ferromagnétique est généralement favorisé[6]. Lorsque plusieurs types d'interaction sont en présence, c'est normalement l'interaction antiferromagnétique qui domine parce qu'elle est indépendante du terme d'échange intra-atomique[7]. Aux cas simples, les règles de Goodenough-Kanamori permettent de prévoir l'échange magnétique net du couplage entre ions. Les complications arrivent en diverses situations :

lorsque les mécanismes d'échange direct et superéchange sont en concurrence ;
lorsque l'angle de liaison cation-anion-cation dévie de 180° ;
lorsque l'occupation des orbitales par les électrons est non-statique ou dynamique ;
lorsque le couplage spin-orbite devient important.

L'échange double est une interaction de couplage magnétique semblable qui a été proposée par Clarence Zener pour expliquer les propriétés de transport électrique. En superéchange cependant, les électrons ne se déplacent pas entre les deux cations métalliques et les nombres d'électrons des deux ions sont égaux ou bien diffèrent par deux. En échange direct par contre, les électrons sont itinérants et se déplacent entre les cations via le ligand intermédiaire (par exemple l'oxygène). Le matériau démontre alors le couplage d'échange magnétique ainsi que la conductivité métallique.

L'oxyde de manganèse (MnO)

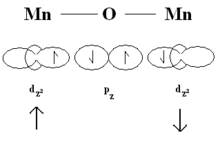
Les orbitales p de l'oxygène et les orbitales d du manganèse peuvent faire un échange direct. Il y a de l'ordre antiferromagnétique parce que l'état singulet est favorisé du point de vue de l'énergie. Cette configuration permet la délocalisation des électrons impliqués qui diminue leur énergie cinétique.

La théorie des perturbations de la mécanique quantique prévoit une interaction antiferromagnétique des spins des atomes de Mn avoisinants, avec l'opérateur d'énergie (hamiltonien).

{\mathcal {H}}_{1,\,2}=+{\frac {2t_{\text{Mn, O}}^{2}\,}{U}}{\hat {S}}_{1}\cdot {\hat {S}}_{2}\,,

où

\,t_{\text{Mn, O}}

est dit l'énergie de saut entre une orbitale 3d de Mn et une orbitale p de O, tandis que U est l'énergie de Mn selon le modèle de Hubbard. Enfin, le facteur

{\hat {S}}_{1}\cdot {\hat {S}}_{2}\,

est le produit scalaire entre les opérateurs du vecteur de spin de Mn à l'hamiltonien de Heisenberg.

Références

H. A. Kramers, Physica 1, 182 (1934).
P. W. Anderson, Phys. Rev. 79, 350 (1950).
J. B. Goodenough, Phys. Rev. 100, 564 (1955).
J. B. Goodenough, J. Phys. Chem. Solids 6, 287 (1958).
J. Kanamori, J. Phys. Chem. Solids 10, 87 (1959).
J. N. Lalena et D. A. Cleary, Principles of Inorganic Materials Design, 2^e éd., John Wiley & Sons, New York, p. 345-346 (2010).
H. Weihe et H. U. Güdel, Inorg. Chem. 36, 3632 (1997).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.