Suite de Conway

La suite de Conway est une suite mathématique inventée en 1986 par le mathématicien John Horton Conway, initialement sous le nom de « suite audioactive »[1]. Elle est également connue sous le nom anglais de Look and Say (« regarde et dis »). Dans cette suite, un terme se détermine en annonçant les chiffres formant le terme précédent.

Définition

Suite de Conway.

Graphe représentant, en ordonnées, le nombre de chiffres du n-ième terme de la suite de Conway, avec n en abscisses, dans un repère semi-logarithmique. Chaque courbe correspond à un terme initial différent : 1 (bleu), 23 (rouge), 13 (violet), 312 (vert). Les courbes tendent vers des droites dont la pente est le logarithme de la constante de Conway.

Le premier terme de la suite de Conway est posé comme égal à 1. Chaque terme de la suite se construit en annonçant le terme précédent, c'est-à-dire en indiquant combien de fois chacun de ses chiffres se répète.

Concrètement :

X_{0}=1

Ce terme comporte simplement un « 1 ». Par conséquent, le terme suivant est :

X_{1}=11

Celui-ci est composé de deux « 1 » :

X_{2}=21

En poursuivant le procédé :

X_{3}=1211

X_{4}=111221

X_{5}=312211

X_{6}=13112221

Et ainsi de suite.

Il est possible de généraliser le procédé en prenant un terme initial différent de 1. Dans le reste de l'article, on supposera que le terme initial vaut 1.

Les 20 premiers termes

	Terme
1	1
2	11
3	21
4	12 11
5	11 12 21
6	31 22 11
7	13 11 22 21
8	11 13 21 32 11
9	31 13 12 11 13 12 21
10	13 21 13 11 12 31 13 11 22 11
11	11 13 12 21 13 31 12 13 21 13 21 22 21
12	31 13 11 22 21 23 21 12 11 13 12 21 13 12 11 32 11
13	13 21 13 21 32 11 12 13 12 21 12 31 13 11 22 21 13 11 12 21 13 12 21
14	11 13 12 21 13 12 11 13 12 31 12 11 13 11 22 21 12 13 21 13 21 32 21 13 31 22 21 13 11 22 11
15	31 13 11 22 21 13 11 12 31 13 11 12 13 21 12 31 13 21 32 21 12 11 13 12 21 13 12 11 13 22 21 23 11 32 21 13 21 22 21
16	13 21 13 21 32 21 13 31 12 13 21 13 31 12 11 13 12 21 12 13 21 13 12 11 13 22 21 12 31 13 11 22 21 13 11 12 31 13 32 11 12 13 21 13 22 21 13 12 11 32 11
17	11 13 12 21 13 12 11 13 22 21 23 21 12 11 13 12 21 23 21 12 31 13 11 22 21 12 11 13 12 21 13 11 12 31 13 32 21 12 13 21 13 21 32 21 13 31 12 13 21 23 12 31 12 11 13 12 21 13 32 21 13 11 12 21 13 12 21
18	31 13 11 22 21 13 11 12 31 13 32 11 12 13 12 21 12 31 13 11 22 11 12 13 12 21 12 13 21 13 21 32 21 12 31 13 11 22 21 13 31 12 13 21 23 22 21 12 11 13 12 21 13 12 11 13 22 21 23 21 12 11 13 12 11 12 13 11 12 13 21 12 31 13 11 22 21 23 22 21 13 31 22 21 13 11 22 11
19	13 21 13 21 32 21 13 31 12 13 21 23 12 31 12 11 13 11 22 21 12 13 21 13 21 22 31 12 11 13 11 22 21 12 11 13 12 21 13 12 11 13 22 21 12 13 21 13 21 32 21 23 21 12 11 13 12 11 12 13 32 21 12 31 13 11 22 21 13 11 12 31 13 32 11 12 13 12 21 12 31 13 11 12 31 12 11 13 31 12 11 13 12 21 12 13 21 13 21 32 11 12 13 32 21 23 11 32 21 13 21 22 21
20	11 13 12 21 13 12 11 13 22 21 23 21 12 11 13 12 11 12 13 11 12 13 21 12 31 13 21 32 21 12 11 13 12 21 13 12 11 22 13 21 12 31 13 21 32 21 12 31 13 11 22 21 13 11 12 31 13 32 21 12 11 13 12 21 13 12 11 13 22 11 12 13 12 21 12 31 13 11 12 31 12 11 23 22 21 12 13 21 13 21 32 21 13 31 12 13 21 23 12 31 12 11 13 11 22 21 12 13 21 13 31 12 13 21 12 31 23 21 12 31 13 11 22 21 12 11 13 12 21 13 12 11 13 12 31 12 11 23 22 11 12 13 21 13 22 21 13 12 11 32 11

Propriétés

La suite de Conway a de multiples propriétés. Certaines d'entre elles sont indiquées ci-dessous, avec, pour les plus simples, les démonstrations correspondantes.

Aucun terme de la suite ne comporte un chiffre supérieur à 3.

Démonstration

Remarquons d’abord que 1, 2 et 3 apparaissent bien (cf X(6) par exemple). Supposons que le chiffre 4 apparaît pour la première fois dans X(n). Il indique une suite de 4 chiffres identiques dans X(n-1) (sinon il aurait déjà été présent dans X(n-1)). Donc X(n-1) contenait xxxx (x= 1, 2 ou 3). Or ceci est impossible car, quelles que soient la position et le contenu de cet ensemble de 4 chiffres identiques, il aurait dû être écrit différemment dans X(n-1). Donc le chiffre 4 ne peut apparaître, ni, par le même raisonnement, les chiffres supérieurs.

Tous les termes de la suite possèdent un nombre pair de chiffres, sauf le terme initial.

Démonstration

Tous les termes de la suite, à l'exception du premier d'entre eux, sont le résultat de la "lecture" du terme précédent. Or cette "lecture" donne par construction une suite de paires de chiffres: par exemple "3" lu donne "13", "111" lu donne "31", "22" lu donne "22", etc.. Donc tout terme (sauf le premier) est constitué de paires de chiffres donc constitué d'un nombre pair de chiffres.

À partir du quatrième terme, les termes de rang pair se terminent par 211 et les termes de rang impair par 221.

Démonstration

Démontrons cette propriété par récurrence. Si X(n) se termine par "211", alors X(n+1) se termine par “x221” donc bien “221”. Si X(n) se termine par "221" alors c’est soit "1221", ce qui donne “x12211” dans X(n+1) donc bien “211”; ou c'est "2221" qui donne "3211" donc bien "211"; ou enfin c'est "3221" qui donne "x32211" donc bien "211". Donc, comme X(4) se termine par 211, X(5) doit se terminer par 221 puis tous les autres X(n) se terminent alternativement par 211 (n pair) ou 221 (n impair).

À partir du huitième terme, les termes commencent cycliquement par "1113", "3113" et "1321".

Démonstration

Remarquons que X(11)= "111312…." puis X(12)="3113… "et X(13)="1321.." commencent respectivement comme X(8), X(9) et X(10).

Plus généralement si X(n) commence par "1113x" (x#3) alors X(n+1) commence par "3113" puis X(n+2) par "1321" et X(n+3) par "111312" ce qui lui donne la même propriété que X(n).

Or X(8) a cette propriété. Donc:

tous les X(n) (n=8+3p) commencent par 1113x x#3 (et même 111312 pour p>0)

tous les X(n) (n=9+3p) commencent par 3113

tous les X(n) (n=10+3p) commencent par 1321

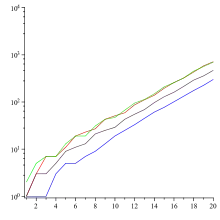
La suite de Conway est strictement croissante, ainsi que celle des L(n) où L(n) est le nombre de chiffres constituant le n-ième terme de la suite de Conway.

Démonstration

On constate que c’est bien le cas pour X(n) jusqu’à X(10) au moins, ainsi que pour L(n) à partir de L(6).

Notons que dans la construction de X(n+1) à partir de X(n), un singleton (un entier isolé) devient une paire (augmentant la longueur L(n) de 1), une paire reste une paire (sans impact sur la longueur) et un triplet (trois entiers identiques consécutifs) devient une paire (diminution de 1 de L(n)).

Démontrons d’abord que L(n+1) est supérieure ou égale à L(n), sachant que ces deux nombres sont pairs (cf propriété précédente).

Pour cela il faut et il suffit que S(n) (le nombre de singletons dans X(n)) soit supérieur ou égal à T(n) (le nombre de triplets de X(n)).

Si X(n) ne contient pas de triplet, la propriété est évidemment vérifiée.

Si X(n) contient au moins un triplet, appelons T(1,n) le premier triplet de X(n) rencontré en partant de la fin de X(n).

Le dernier chiffre de X(n) est de rang pair, car L(n) est pair. Comme le premier et le dernier chiffres de tout triplet sont de rang impair, il y a donc un nombre impair de chiffres entre T(1,n) et la fin de X(n). Donc au moins 1 singleton (puisqu’il ne peut par hypothèse y avoir de triplet entre T(1,n) et la fin de X(n)). En répétant le raisonnement sur T(2,n) et les suivants on démontre bien qu’il y a toujours au moins un singleton derrière un triplet, situé avant le triplet suivant s’il y en a un. Donc au moins autant de singletons que de triplets dans X(n). Donc L(n+1) est supérieure ou égale à L(n).

Donc tout X(n) a au moins autant de singletons que de triplets dans sa partie commençant par son premier triplet (en partant de la gauche).

Or la propriété relative aux premiers chiffres de X(n) montre que tous les X(n) commencent soit par un singleton, soit par "111" suivi de 2 singletons: donc dans tous les cas X(n) a plus de singletons que de triplés. Donc L(n) est une suite strictement croissante (n>=6) , et, par conséquent, X(n) également.

En moyenne, les termes de la suite possèdent 50 % de chiffres 1, 31 % de 2 et 19 % de 3.
Le nombre $L_{n}$ de chiffres du n-ième terme de la suite est équivalent à Cλⁿ, où λ ≈ 1,303 577[2] est un entier algébrique de degré 71 nommé constante de Conway[3] - [4], et C est une autre constante. En particulier :
$\lim _{n\to +\infty }{\frac {L_{n+1}}{L_{n}}}=\lambda$

Cette propriété reste vraie dans le cas général[5] où le premier terme de la suite est choisi différent de 1 (et de 22, puisque dans ce cas la suite est constante), avec une constante C qui dépend de ce choix, mais avec toujours la même constante λ.

Racines du polynôme de Conway dans le plan complexe.

La constante de Conway est l'unique solution réelle positive de l'équation polynomiale suivante[6] :

{\begin{aligned}&\,\,\,\,\,\,\,x^{71}&&&&-x^{69}&&-2x^{68}&&-x^{67}&&+2x^{66}&&+2x^{65}&&+x^{64}&&-x^{63}\\&-x^{62}&&-x^{61}&&-x^{60}&&-x^{59}&&+2x^{58}&&+5x^{57}&&+3x^{56}&&-2x^{55}&&-10x^{54}\\&-3x^{53}&&-2x^{52}&&+6x^{51}&&+6x^{50}&&+x^{49}&&+9x^{48}&&-3x^{47}&&-7x^{46}&&-8x^{45}\\&-8x^{44}&&+10x^{43}&&+6x^{42}&&+8x^{41}&&-5x^{40}&&-12x^{39}&&+7x^{38}&&-7x^{37}&&+7x^{36}\\&+x^{35}&&-3x^{34}&&+10x^{33}&&+x^{32}&&-6x^{31}&&-2x^{30}&&-10x^{29}&&-3x^{28}&&+2x^{27}\\&+9x^{26}&&-3x^{25}&&+14x^{24}&&-8x^{23}&&&&-7x^{21}&&+9x^{20}&&+3x^{19}&&-4x^{18}\\&-10x^{17}&&-7x^{16}&&+12x^{15}&&+7x^{14}&&+2x^{13}&&-12x^{12}&&-4x^{11}&&-2x^{10}&&+5x^{9}\\&&&+x^{7}&&-7x^{6}&&+7x^{5}&&-4x^{4}&&+12x^{3}&&-6x^{2}&&+3x&&-6\\&=0.\end{aligned}}

« Désintégration audioactive »

John Conway qualifia initialement cette suite de « désintégration audioactive » (audioactive decay en anglais), un jeu de mots sur la désintégration radioactive, en remarquant le comportement des différents termes de la suite.

Dans son théorème cosmologique[4], il démontra qu'à partir d'un certain point, presque tous les termes de la suite peuvent être décomposés en 92 sous-termes (nommés éléments, par analogie avec les éléments chimiques) qui se décomposent au terme suivant en un certain nombre d'autres éléments.

Par exemple, l'élément le plus simple, nommé hydrogène, est la séquence $22$ qui donne elle-même au terme suivant. La séquence $3113322112$ est dénommée manganèse ; au terme suivant, elle donne $1321232221112$ qui se décompose en les séquences prométhium ( $132$ ) et sodium ( $123222112$ ).

Il a été montré que si l'on débute la suite par le terme uranium $3$ , les 91 autres éléments seront apparus dans un terme ou un autre au bout de 91 itérations. Cette suite porte d'ailleurs en anglais le nom de Conway's sequence.

Dans la littérature

Bernard Werber a repris cette suite dans ses œuvres Les fourmis et dans L'Encyclopédie du savoir relatif et absolu[7].

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Look-and-say sequence » (voir la liste des auteurs).

(en) John H. Conway, « The Weird and Wonderful Chemistry of Audioactive Decay », Eureka, Université de Cambridge, n^o 46,‎ 1986, p. 5-18 (ISSN 0071-2248).
Pour plus de décimales, voir la suite A014715 de l'OEIS - jusqu'à la 20000^e.
(en) Eric W. Weisstein, « Conway's Constant », sur MathWorld.
« A Derivation of Conway’s Degree-71 “Look-and-Say” Polynomial », sur Nathaniel Johnston, 1^er novembre 2010 (consulté le 4 avril 2021)
(en) Michael J. Bradley, Ph.D., Mathematics Frontiers: 1950 to the Present, Infobase Publishing, 1997 (ISBN 978-0-8160-5427-5, lire en ligne), p. 45.
Suite A137275 de l'OEIS.
[vidéo] Deux (deux ?) minutes pour les suites de Conway sur YouTube

Annexes

Liens externes

(en) Look and Say sequence: describe the previous term! (method A - initial term is 1) : suite A005150 de l'OEIS
(en) Eric W. Weisstein, « Look and Say Sequence », sur MathWorld
(en) Henry Bottomley, « Evolution of Conway's 92 Look and Say audioactive elements » : une compilation des 92 éléments « audioactifs » de la suite
Des algorithmes de générations en différents langages sur Rosetta Code

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

Suite de Conway

Définition

Les 20 premiers termes

Propriétés

« Désintégration audioactive »

Dans la littérature

Références

Annexes

Articles connexes

Liens externes