Siteswap
Le siteswap est une notation de jonglerie qui décrit le rythme des lancers et donc la trajectoire des objets dans l’espace. Elle s’est imposée comme langage de référence pour décrire et communiquer les séquences de jonglerie intéressantes en solo et à plusieurs jongleurs. La notation consiste en une suite de chiffres codant chaque lancer le nombre de temps s’écoulant jusqu’à la relance du même objet. Ceci permet de modéliser et d’inventer une infinité de séquences, quel que soit le nombre d’objets ou de sites de lancer (de mains par exemple, mais pas uniquement). Malgré sa rudesse mathématique décriée par certains jongleurs, le siteswap a largement contribué à enrichir le répertoire des figures de jonglerie.
Le siteswap est particulièrement adaptée aux techniques de lancer : balles, massues et anneaux principalement. Néanmoins, les lancers peuvent aussi bien être interprétés comme un blocage en contact sur le corps, un roulement sur le sol, un ou plusieurs rebonds sur une surface, etc. Le siteswap peut également être adapté pour décrire des techniques de diabolo.
Historique de la notation
La notation la plus simple, souvent nommée vanilla siteswap dans les pays anglo-saxons, décrit le mode de jonglerie asynchrone à deux mains. Elle est inventée par trois groupes indépendants. Le premier en 1981 à Santa Cruz est Paul Klimek avec son Quantic Juggling[1]. En 1985 à Cambridge en Angleterre, Mike Day, Colin Wright et Adam Chalcraft inventent une notation similaire qu’ils nomment notation de Cambridge. À la même époque, Bruce Tiemann au California Institute of Technology en Californie, qui n'avait jamais entendu parler de ces systèmes de notation, invente une méthode pour trouver les figures qu'il nomme « site swaps » car sa méthode pour les générer est basée sur le fait d’échanger « tels objets à tels endroits [sites de lancer] dans le temps et l’espace ».
La liste de diffusion rec.juggling en activité depuis sur Usenet[2] et les débuts d’Internet permirent la diffusion rapide de ces notions parmi la communauté des jongleurs scientifiques. rec.juggling reste aujourd’hui la source d’information la plus complète sur le siteswap : premiers diagrammes états-transitions, annonce et souvent publication de l’essentiel des travaux mathématiques liés à la notation ainsi que de nombreux conseils pour les jongleurs dans la pratique.
De simples conventions typographiques permettent d’adapter le siteswap vanille original pour décrire le passing, le mode de jonglerie synchrone ainsi que les lancers multiplexs. En 1991 la notation multi-mains d’Ed Cartsen (multi-hand notation ou mhn) synthétise la plupart des notions connues car elle permet de décrire l’asynchrone avec la même notation que le synchrone quel que soit le nombre de sites de lancer. Depuis les années 1990, Jack Boyce aide au développement des notations synchrone, multiplex et passing grâce à ses recherches et son logiciel de simulation de jonglage JugglingLab. Ben Beever (1976-2015), professeur de mathématique anglais, est le premier à utiliser l’astérisque (*) pour noter les figures synchrones dans son livre Siteswap Ben’s Guide to Juggling Pattern de 1999.
La notation multimain sert par exemple dès la fin des années 1990 à la troupe Gandini Juggling pour réaliser des séquences siteswaps en passing avec un nombre impair de mains ou encore vers 2002 aux diabolistes dont la ficelle peut servir de site de lancer (mhn avec un seul site de lancer). En 2005, la mhn est toujours suffisante pour décrire le mode de jonglage polyrythmique.
Les bases : le siteswap asynchrone
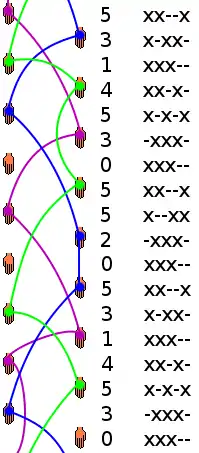
La forme la plus commune du siteswap, appelée vanilla siteswap dans les pays anglo-saxons, décrit les séquences où les lancers sont asynchrones (alternent entre la main gauche et la main droite) et où une seule balle est lancée à la fois. Si l’on filmait en plongée un jongleur lançant successivement chaque balle en alternant entre la main gauche et la main droite tandis qu’il avance, on pourrait voir quelque chose qui ressemblerait au diagramme de droite, diagramme que l’on appelle parfois diagramme d’espace temps par analogie avec son équivalent en physique.
Pour décrire la séquence, on détermine pour chaque étape combien de temps plus tard l’objet sera relancé. Par exemple, si l’on considère le diagramme de droite, au premier lancer, la balle violette est lancée par la main droite, puis la balle bleue, puis la verte, à nouveau la verte, à nouveau la bleue et enfin la balle violette est rattrapée et relancée par la main gauche au cinquième temps : cela confère au premier lancer la valeur de 5. En répétant l’opération pour chaque temps, on obtient une séquence de nombres qui dénote pour chaque lancer le nombre de temps écoulés jusqu’à la relance. Étant donné que les lancers alternent de main en main, les nombres impairs désignent des lancers d’une main à l’autre (lancers croisés), tandis que les nombres pairs retombent dans la main qui les a lancés (lancers décroisés). Un 3 correspond au nombre de temps d’un lancer de cascade à trois objets. Un 4 correspond à celui d’une fontaine à 4 objets, etc.
Le nombre associé à chaque lancer permet de déterminer le nombre de temps que la balle passera en l’air et ainsi d’évaluer la hauteur relative du lancer. C’est pourquoi beaucoup interprètent les nombres comme des hauteurs :
- le 3 correspond à la hauteur des lancers lorsque l’on jongle à 3 balles (croisé)
- le 4 correspond à la hauteur des lancers lorsque l’on jongle à 4 balles (non croisé)
- le 5 correspond à la hauteur des lancers lorsque l’on jongle à 5 balles (croisé)
et ainsi de suite…
Ce raccourci, bien que techniquement incorrect, est particulièrement utile dans la pratique puisqu’il permet de produire du premier coup la séquence sans avoir à penser à l’ensemble des permutations mises en jeu. Ce raccourci ne vaut que pour les techniques de jonglerie strictement aériennes et ne décrit en aucun cas une hauteur absolue (celle-ci dépendant du tempo).
On note trois lancers particuliers :
- le 0 correspond à un temps où la main est vide et en attente ;
- le 1 correspond à un objet rapidement passé à l’autre main pour être aussitôt relancé (la passe pouvant se faire en lançant la balle à proprement parler ou non) ;
- le 2 correspond généralement à un objet maintenu dans la main, cependant il est possible de l’exprimer par un lancer décroisé Les lancers supérieurs à 9 sont notés par des lettres, en commençant par A : 8, 9, A, B, C… (A = 10, B = 11… comme pour une base hexadécimale).
Chaque séquence est amenée à se répéter après un certain nombre de lancers appelé période. La séquence est ainsi notée par le plus petit segment représentatif et non-répétitif : la séquence de droite est ainsi notée 53 145 305 520 et a une période de 11. Quand la période est impaire (comme dans cet exemple), la séquence sera dite symétrique parce qu’elle sera répétée à partir de l’autre main. Les séquences de période paire sont dites asymétriques, chaque main répétant sans cesse les mêmes types de lancer.
Le nombre d’objets nécessaires pour jongler la séquence est la moyenne arithmétique des nombres de la notation. Ainsi, 441 est jonglé avec 3 objets car (4+4+1)/3 = 3, 86 sera jonglé avec 7 objets car (8 + 6)/2 = 7, 7531 avec 4 etc. Toute séquence valide a donc une moyenne arithmétique entière, mais ce n’est qu’une condition nécessaire et non suffisante. Toute séquence ayant une moyenne arithmétique entière est réorganisable en une séquence valide suivant le théorème de réorganisation[3].
Par convention, on note le siteswap en commençant par les nombres les plus grands. Ainsi les siteswaps 315, 153 et 531 seront uniformément notés 531.
État, transition et diagramme états-transitions
Une séquence siteswap détermine un enchaînement de lancers dans le temps (point de vue diachronique). Mais il est également possible pour chaque temps de décrire l’état des objets en l’air, c’est-à-dire déterminer les temps auxquels chaque objet sera rattrapé et relancé (point de vue synchronique).
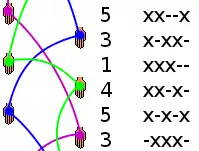
On associe ainsi à chaque temps un état en marquant chaque point du temps où l’objet sera rattrapé par un x et chaque point du temps où rien n’est encore prévu par un -. Considérons par exemple l’état des balles juste après le premier lancer dans le diagramme de droite. Nous savons qu’une balle atterrira au temps suivant, puis tout de suite une autre et enfin, nous venons de lancer une balle qui atterrira au cinquième temps. On note ainsi l’état xx—x et on lit de gauche à droite en suivant la flèche du temps. On peut maintenant se servir de cet état pour déterminer les possibilités du prochain lancer. Nous commencerons par enlever le x sur la gauche (la balle qui atterrit au prochain temps) et rajouter un - sur la droite. On obtiendra ainsi x—x- : ceci correspond à l’état virtuel des balles lorsque le jongleur a rattrapé la balle mais ne l’a pas encore relancée. Grâce à cette opération nous pouvons déterminer exhaustivement les lancers possibles. Comme nous venons de rattraper une balle, nous ne pouvons faire un 0. Nous ne pouvons pas non plus faire un 1 puisque nous avons déjà une balle qui sera rattrapée pour ce temps (le premier x). Il en va de même pour le 4 (quatrième x). Nous pouvons par contre effectuer un 2, un 3 ou un 5. Si, comme le jongleur du diagramme nous choisissons de faire un 3, l’état suivant sera x-xx- (il suffit de remplacer le - en position 3 par un x).
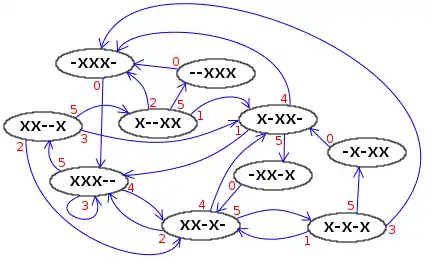
De cette façon il est possible de faire l’inventaire de tous les états possibles pour un nombre d’objets donné et une valeur maximale de lancer donnée et de déterminer les lancers possibles à partir de chaque état. Le diagramme de gauche montre tous les états possibles pour 3 objets et un lancer maximal de 5. Ce diagramme répertorie ainsi tous les siteswaps possibles dans ces conditions. Il suffit de partir d’un état et de suivre les flèches à sa guise et lorsque l’on est revenu au point de départ on a obtenu un siteswap valide. Tous les siteswap peuvent être répertoriés par ce biais. Cependant, le diagramme devient vite extrêmement complexe à mesure qu’augmente la hauteur des lancers. On utilise alors d’autres types de diagramme d’état.
| 7 | 11 | 13 | 14 | 19 | 21 | 22 | 25 | 26 | 28 | |
| (7) 111 | 3 | 4 | 5 | |||||||
| (11) 1011 | 2 | 4 | 5 | |||||||
| (13) 1101 | 1 | 4 | 5 | |||||||
| (14) 1110 | 0 | |||||||||
| (19) 10 011 | 2 | 3 | 5 | |||||||
| (21) 10 101 | 1 | 3 | 5 | |||||||
| (22) 10 110 | 0 | |||||||||
| (25) 11 001 | 1 | 2 | 5 | |||||||
| (26) 11 010 | 0 | |||||||||
| (28) 11 100 | 0 | |||||||||
| Table états-transitions pour 3 objets, valeur de lancer maximum 5. | ||||||||||
La notation des états est de fait binaire, pour chaque temps il n’est que deux valeurs possibles : souvent on écrit 0 et non - et 1 au lieu de x. Ainsi, l’état x x - - x peut être noté 11 001. On peut même le convertir en système décimal et le noter 25. Cependant, pour des raisons techniques d’allègement des calculs, lorsqu’on passe au système binaire, il est d’usage d’opérer une seconde transformation. Étant donné que le bit faible se lit à droite dans la notation binaire et qu’il est le plus à même de correspondre à un objet rattrapé au temps suivant, on change le sens d’écriture. Ainsi, l’état noté x x - - x dans les diagrammes précédents sera finalement noté 10 011 et non 11 001 et correspondra à 19 et non 25 en système décimal. Ainsi le décalage temporel opéré pour déterminer les possibilités du prochain lancer correspondra à une simple division entière par deux (l’état virtuel suivant sera 9 ou 1001, précédemment noté x - - x -). La table états-transitions utilise cette transformation : elle contient sous une autre forme les mêmes informations que le diagramme précédent. Les lignes donnent tous les lancers possibles pour changer d’état et les colonnes indiquent l’état résultant. Comme pour le diagramme précédent, lorsqu’on revient à l’état de départ, on a produit un siteswap valide.
Mathématiquement, on dira que ce qu’on appelle communément un lancer est en réalité une permutation de l’ensemble que constitue un état, que le nombre d'éléments de cet ensemble correspond à la longueur maximale des lancers. Une séquence siteswap sera ainsi une composition de permutations dont le résultat est une permutation identique. On retrouve ainsi le sens littéral du mot siteswap (permutation de sites).
Il faut également noter que le siteswap vanille n’est pas limité à deux mains : il n’y a aucune limite au nombre de sites, cependant la condition selon laquelle les lancers sont successifs rend son utilisation difficile pour décrire les séquences incluant plus d’un jongleur.
Siteswaps asynchrones et synchrones
La forme vanilla de la notation siteswap se limite à la description de figures asynchrones : les deux mains lancent alternativement les objets. Chaque main lance donc tous les deux temps. Mais la jonglerie inclut également un non moins vaste éventail de figures synchrones, les lancers se faisant simultanément des deux mains. Dans ce cas, étant donné que pour chaque temps il y a deux lancers, on note les deux lancers entre parenthèses et séparés par une virgule, par exemple (4,4). Pour des raisons de commodité et de cohérence, on note le siteswap synchrone en doublant à chaque fois la longueur du lancer. Ainsi, une fontaine synchrone à quatre objets devrait théoriquement s’écrire (2,2) chaque balle étant relancée tous les deux temps, mais on écrit (4,4) pour :
- Garder la correspondance avec le siteswap vanille (ainsi en faisant cette correction un 4 en siteswap synchrone sera équivalent à un 4 en siteswap vanille).
- Conserver la règle de la moyenne arithmétique qui permet de calculer le nombre d’objets nécessaires à la réalisation de la séquence (ainsi pour un (4,4) il faudra (4 + 4) / 2 = 4 objets).
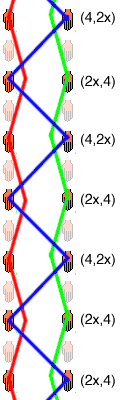
Par suite de ce doublement, dans le siteswap synchrone, seuls les chiffres pairs seront utilisés. On peut se représenter cette multiplication comme l’ajout systématique d’un temps fantôme entre chaque temps, comme sur le diagramme de droite : pour tout siteswap (vanille ou synchrone), chaque main lancera tous les deux temps. Lorsque les lancers sont croisés, on ajoute un x après le chiffre. Par exemple, (4,2x)(2x, 4) est la boîte à trois objets représentée sur le diagramme de droite.
Un siteswap synchrone peut comporter un * à la fin de sa séquence ; ce dernier signifie que la séquence présentée doit s’effectuer en inversant alternativement les mains droites et gauches. Ainsi, (4,2X)(2X, 4) se note (4,2X)*, et (6X, 4)(4,2X)* correspond à (6X, 4)(4,2X)(4,6X)(2X, 4).
Mathématiquement, l’introduction de la synchronie dans le siteswap équivaut à ajouter une dimension supplémentaire aux états possibles. À la dimension temporelle on rajoute celle des mains ou sites mis en jeu. On peut ainsi inclure un nombre quelconque de mains et donc de jongleurs. Dans ce cas on rajoutera les lancers de chaque site entre virgules dans les parenthèses délimitant l’ensemble des lancers pour un temps : (4,4,4,4) décrit deux jongleurs jonglant à quatre balles.
Déterminer la validité d’une séquence
Une séquence n’est valide qu’à la condition d’être jonglée avec un nombre entier d’objets. Mais il s’agit simplement d’une condition nécessaire et non suffisante. La règle de la moyenne sera ainsi un bon test préliminaire compte tenu de la simplicité du calcul, mais elle ne sera jamais une démonstration suffisante. Par exemple 432 se jonglerait à trois balles mais n’est pas valide.
La règle fondamentale exige qu’une seule balle puisse être lancée (ou rattrapée - deux faces équivalentes d’un même principe) à la fois. Ainsi une séquence sera valide si et seulement si tous les lancers interviennent dans des temps différents. À partir de ce postulat, on peut imaginer diverses méthodes de vérification.
Remarque : ce principe s’applique à la forme vanille du siteswap et mutatis mutandis à sa forme synchrone (il s’agira dans ce cas de vérifier que chaque main ne lance qu’une seule balle à la fois), mais il va de soi que les règles de validation d’un siteswap multiplex seront fondamentalement différentes.
Méthode brute
La méthode brute consistera à faire l’inventaire de tous les temps de relance pour s’assurer qu’à chaque lancer correspondra un temps différent. Ainsi pour vérifier la validité de 758 514 :
siteswap : 7 5 8 5 1 4 7 5 8 5 1 4 7 5 8 5 1 4. ..
temps où la balle est lancée : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17. ..
temps de relance : 7 6 10 8 5 9 13 12 16 14 11 15 19 18 22 20 17 21. ..
Le temps de la relance correspond à la somme de la valeur du lancer et du temps auquel ce lancer a lieu.
Dans cet exemple, on constate que les temps de relance sont tous différents : chaque balle est lancée en son temps et il n’y a pas de collision dans la main - le siteswap 758 514 est ainsi un siteswap valide.
Pour 578 514, qui pourtant se jonglerait avec un nombre entier de balles, on observe tout de suite une incohérence :
siteswap : 5 7 8 5 1 4 5 7 8 5 1 4. ..
temps où la balle est lancée : 0 1 2 3 4 5 6 7 8 9 10 11. ..
temps de relance : 5 8 10 8 5 9 11 14 16 14 11 15. ..
Les lancers 2 et 4 seront tous deux relancés au 8e temps, ce qui contredit un principe fondamental. La séquence 578 514 n’est donc pas valide.
Modulation
La méthode classique consistera à éviter de faire de longs calculs qui obligent à répéter plusieurs fois la séquence pour s’assurer de la validité. On se contente de calculer les temps de relance pour les p premiers lancers (où p est la période de la séquence siteswap) que l’on modulera par la période (on gardera le reste de la division entière par la période). Si l’ensemble obtenu est une permutation de {0;1;2;… ;p-1} (plus simplement dit : si tous les nombres obtenus sont différents), alors la séquence est valide.
séquence siteswap : 7 5 8 5 1 4
temps où la balle est lancée : 0 1 2 3 4 5
temps de relance : 7 6 10 8 5 9
modulation par la période (ici 6) : 1 0 4 2 5 3
{1;0;4;2;5;3} est une permutation de {0;1;2;3;4;5}, la séquence siteswap 758 514 est par conséquent valide.
séquence siteswap : 5 7 9 4 0 5
temps où la balle est lancée : 0 1 2 3 4 5
temps de relance : 5 8 11 7 4 10
modulation par la période (ici 6) : 5 2 5 1 4 4
Il y a au moins une répétition, par conséquent la séquence siteswap 579 405 n’est pas valide.
Caractérisation des séquences
Une séquence siteswap est dite fondamentale lorsque cette séquence peut être effectuée directement à partir de l’état de base (autrement dit, lorsqu’on peut l’enchaîner directement et sans transition depuis la cascade ou fontaine de base correspondant au nombre d’objets). 441 est ainsi une séquence fondamentale : on peut enchaîner directement un 441 après une cascade 3, puis revenir directement en cascade 3. Par suite, toutes les séquences fondamentales pour un nombre d’objets donné s’enchaînent entre elles sans transition : 531, 441 et 423 peuvent ainsi s’enchaîner dans n’importe quel ordre, par exemple 531 531 441 423 423.
Une séquence siteswap est dite excitée lorsqu’elle n’est pas fondamentale, c’est-à-dire lorsqu’elle ne peut être enchaînée directement à partir de l’état de base et qu’elle nécessite une transition pour entrer et sortir. La douche à trois objets 51 est ainsi une séquence excitée car il n’est pas possible d’enchaîner 3 et 51, il faut effectuer une transition, par exemple : 3 (4) 51 (2) 3. Les transitions sont données entre parenthèses.
Une séquence siteswap est dite première lorsqu’elle ne peut être divisé en plusieurs séquences indépendantes et répétables, une autre manière de la caractériser est de dire qu’elle ne passe jamais deux fois par le même état. Ainsi 3, 441 et 633 sont des séquences siteswap premières, alors que 423 n’en est pas une puisqu’elle se décompose en 42 et 3. Une séquence première peut aussi bien être excitée (par exemple 51 ou 741) que fondamentale (par exemple 642 ou 97 531).
Les lancers multiplex
Un lancer multiplex correspond au lancer simultané de plusieurs objets par une même main. La notation étendue du siteswap utilise les crochets pour décrire les multiplex. Par exemple [54] signifie que la main lance deux objets en même temps : l’un en 5 l’autre en 4.
Comme pour le siteswap vanille chaque nombre est représenté par un caractère unique, le nombre de caractères présents entre les crochets correspond donc au nombre d’objets nécessaires pour réaliser le lancer multiplex. Les jongleurs utilisent une nomenclature spécifique en fonction du nombre d’objets impliqués dans le multiplex :
- [54] est un duplex,
- [432] est un triplex,
- [6543] est un quadruplex,
- [97 531] est un quintuplex…
Comme expliqué précédemment le 0 définit l’absence d’objet dans la main au moment du lancer. Bien qu’il soit possible de décrire indéfiniment d’invisibles balles supplémentaires dans la main, par exemple [40 000], il est de bon sens de réduire ces expressions au plus simple c’est pourquoi le 0 n’est pas utilisé à l’intérieur des crochets, dans notre exemple [4000] est l’équivalent de 4. Le même bon sens nous mène à exclure l’utilisation de crochets à l’intérieur d’autres crochets, par exemple [5[43]2] est un non-sens la bonne écriture pour ce multiplex est en fait [5432].
Selon les logiciels et les coutumes locales les lancers sont triés entre les crochets par ordre croissant ou décroissant (le plus courant). Pour distinguer ces lancers à l’oral et marquer la différence avec les lancers classiques les jongleurs ont pris l’habitude de nommer l’action comme un nombre complet. Par exemple [43]23 sera prononcé : quarante trois - deux - trois.
Règles mathématiques
La notation multiplex a été développée pour étendre le siteswap vanille mais son fonctionnement peut être retranscrit pour l’ensemble des notations : notation synchrone, notation mhn. Notez que dans ce cas, les états ne seront plus binaires, mais écrit dans un autre système de numération (ternaire, quaternaire ou plus encore).
Les règles applicables aux siteswap vanilles, synchrone et mhn s’applique toujours avec les multiplex. Cependant il faut intégrer la notion de lancer simultané et éviter les pièges. Prenons l’exemple de la règle de la moyenne [43]23, j’additionne les lancers 4+3+2+3=12, je divise par le nombre de temps 12/3=4, cette séquence se jongle donc à 4 balles. La séquence comporte 4 lancers pour 3 temps à la différence d’une séquence vanille pour lesquelles nombre de lancers et nombre de temps sont égaux.
La notation multiplexes décrit en fait la superposition de deux couches jonglées. Cette constatation permet de travailler plus facilement sur les séquences en les concaténant, par exemple 423 + 300 = [43][20][30] soit [43]23.
(à finir) Vérification Mod, méthode +p, interruption, méthode +n, lancer initiant
Les bras croisés
Il est possible d’ajouter à cette notation de nombreuses informations, dont la position des bras. Dérivé du MMSTD (Mill's Mess State Transition Diagram) de Mike Day, le système OSU de Sylvain Garnavault, propose les suffixes suivants :
- S pour « side » représente les bras décroisés.
- O pour « over » représente les bras croisés, la main qui lance au-dessus.
- U pour « under » représente les bras croisés, la main qui lance en dessous.
Exemples avec la séquence siteswap 3 :
- S représente une simple cascade.
- S U représente un moulin par-dessous.
- S U O représente un demi Mills mess (voir figures de jonglerie aérienne) : les lancers sont des 3 mais correspondent alternativement à un lancer decroisé, en dessous puis au-dessus.
- S O représente un moulin par-dessus.
- S O U représente un demi funky mess.
Les limites du siteswap
Cette notation reste un outil ne notant que l’ordre de succession des lancers. Contrairement à ce qui lui a été reproché, elle ne limite pas la créativité des jongleurs, ni le côté artistique de la jonglerie. Elle permet au contraire des échanges plus faciles entre les jongleurs.
Il reste de nombreuses variantes non précisées par le siteswap :
- Les lancers autour du corps (dans le dos, sous la jambe, au-dessus de l’épaule…) ;
- Les différents types de lancers et rattrapage possibles (en patte de chat, en pingouin, sur le dos de la main…) ;
- Les gestes et acrobaties accompagnant les temps morts (pirouettes, sauts périlleux, révérences…) ;
- Les variantes spécifiques aux agrès (1 tour, 2 tours, à plat, sur le plan parallèle au corps etc. pour les massues, les lancers en crêpe pour les anneaux…)
On peut voir le siteswap comme le solfège de la jonglerie. L’exclusion de certains aspects et son abstraction font à la fois sa force et sa faiblesse. Le siteswap n’épuise de loin pas toutes les figures possibles, mais il en décrit d’avance la structure et note avec une grande économie une bonne partie d’entre elles. L’inventivité dans l’utilisation du siteswap consiste justement à en développer les variations. Par ailleurs, diverses extensions ont été proposées pour affiner le caractère descriptif du siteswap, comme le siteswap généralisé qui ajoute un nombre indéfini de dimensions à une séquence siteswap où peuvent dès lors être notées la plupart des indications de mouvement, de style etc.
Logiciels de simulation
Il existe un grand nombre de programmes informatiques permettant de simuler des séquences siteswap :
- Juggling Lab animator, le programme de référence, un simulateur open source écrit en Java capable d’interpréter quasiment toutes les syntaxes de siteswap. Il peut également être inclus sur une page web sous la forme d’un applet. Il gère le passing, les multiplex, les mouvements de mains personnalisés et permet de générer des siteswap ;
- DSSS, un simulateur de siteswap en flash appliqué au diabolo ;
- Jaggle, un autre simulateur en java, en 3 d, capable de gérer les mouvements de main et de repasser les figures à l’envers ;
- Jongl, un simulateur développé pour un grand nombre de systèmes d’exploitation. Il est particulièrement soigné dans ses graphismes 3 d et gère les séquences de passing
- JoePass, un simulateur 3 d pour Os 9, Os X et Windows, conçu spécialement pour le passing avec une grande bibliothèque de séquences, la possibilité de visualiser les diagrammes de cause et de simuler des séquences en notation multi-main (mhn).
Notes et références
- ou Quantum Juggling.
- Statistiques de rec.juggling
- Benoît Guerville, Théorème de réorganisation, janvier 2009.
Bibliographie
(en) Burkard Polster, The Mathematics of Juggling, Springer, 2003. (ISBN 978-0-387-95513-1).
Articles connexes
Fondements mathématiques du siteswap
- La théorie des ensembles et la combinatoire fournissent les bases de la notion d’état, permettent de les dénombrer et de décrire les permutations opérées.
- La théorie des graphes et les matrices sont utilisées pour étudier les diagrammes de transition d’états (ceux-ci étant des graphes orientés et valués) et les tables de transition (celles-ci étant des matrices d’adjacence particulières) et en explorer certaines propriétés (nombre de cycles, cycles les plus longs…).
- La théorie des groupes, en particulier les groupes de Weyl mais aussi la théorie des tresses permettent d’étudier les permutations mises en jeu.
Articles théoriques sur les notations utilisées en jonglerie
- Article notation, répertoriant les différentes notations utilisées en jonglerie.
- Article sur les diagrammes, présentant les représentations graphiques les plus communes.
Applications spécifiques aux diverses disciplines de la jonglerie
- Article diabolo, décrivant l’utilisation du siteswap vanille dans le domaine du diabolo.
- Article rebond sur l’utilisation du siteswap dans la jonglerie à rebond et les extensions utilisées pour noter les divers types de lancer.
- Article passing sur l’utilisation des différentes formes de siteswap au passing et les extensions introduites pour décrire les séquences incluant plus d’un jongleur.
Liens externes
- (fr) Les mathématiques du jonglage par Vincent Pantaloni - Présentation grand public assez complète des mathématiques du jonglage : siteswap, graphes de transition, théorème de Shannon.