Réseau neutre (évolution)
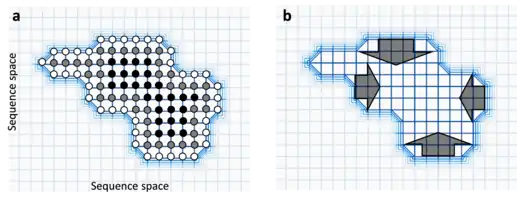
Un réseau neutre correspond à un groupe de gènes tous liés par des mutations ponctuelles et possédant une fonction ou fitness équivalente[1]. Chaque nœud du réseau représente une séquence génique et chaque arête représente une mutation liant deux séquences. Les réseaux neutres peuvent être considérés comme des plateaux hauts et plats dans un paysage adaptatif[A 1]. Au cours de l'évolution neutre, les gènes peuvent se déplacer aléatoirement à travers des réseaux neutres et traverser des régions d'espace de séquence[A 2], ce qui peut avoir des conséquences sur la robustesse et l'évolvabilité.
Causes génétiques et moléculaires
Les réseaux neutres existent dans les paysages de fitness car les protéines sont robustes aux mutations. Cela mène à des réseaux de gènes étendus et de fonction équivalente, liés par des mutations neutres[2] - [3]. Les protéines sont résistantes à des mutations car de nombreuses séquences peuvent se replier dans des structures de repliement hautement semblables[4]. Une protéine adopte un ensemble limité de conformations natives car ses conformères ont une énergie plus faible qu'à des états non repliés ou mal repliés (voir le ΔG du repliement)[3] - [5]. Cela est réalisé par un réseau interne et distribué d'interactions coopératives (hydrophobes, polaires et covalentes). La robustesse structurelle des protéines résulte de quelques mutations uniques étant suffisamment perturbatrices pour compromettre la fonction. Les protéines ont également évolué afin d'éviter l'agrégation[6], car des protéines partiellement repliées peuvent combiner pour former des masses et des fibrilles protéiques de grosse taille, répétées et insolubles. Il a été montré que les protéines montrent des caractéristiques de conception négatives pour réduire l'exposition aux motifs en feuillets bêta à tendance agrégatoire au sein de leurs structures[7]. De plus, des études ont montré que le code génétique en lui-même peut être optimisé de telle façon que la majorité des mutations ponctuelles mènent à des acides aminés similaires (conservatives)[7] - [8]. Ensemble, ces facteurs créent une distribution des effets de la fitness des mutations, distribution qui contient une grande proportion de mutations neutres et quasi-neutres[9].
Évolution
Les réseaux neutres sont un sous-ensemble de séquence dans l'espace de séquence qui ont une fonction équivalente, et ainsi forment un plateau large et plat au sein du paysage de la fitness. L'évolution neutre peut ainsi être vue comme une population se dispersant à partir d'un groupe de nœuds de séquences, à travers le réseau neutre, jusqu'à un autre groupe de nœuds de séquences. Comme on pense que la majorité des événements évolutifs sont neutres[10] - [11], une large proportion de changements géniques entraîne le mouvement à travers des réseaux neutres étendus.
Robustesse
Plus une séquence contient de voisins (séquences avoisinantes) neutres, plus elle sera robuste aux mutations car celles-ci sont plus à même de simplement la convertir de façon neutre en une séquence fonctionnellement équivalente. En effet, s'il y a de grosses différences entre le nombre de voisins neutres de différentes séquences au sein d'un réseau neutre, la population devrait évoluer vers des séquences robustes. On appelle parfois cela la circum-neutralité (circum-neutrality en anglais), et représente le mouvement de populations loin des "falaises" du paysage de la fitness[12].
Outre les modèles in silico[1], ces processus commencent à être confirmés par l'évolution expérimentale du cytochrome P450[13] et la β-lactamase[14].
Évolvabilité
L'intérêt d'étudier l'interaction entre la dérive génétique et la sélection est né vers les années 1930, lorsque la théorie du décalage-équilibre a proposé que dans certaines situations, la dérive génétique pourrait faciliter une évolution adaptative par la suite[15]. Bien que les détails de la théorie soient largement discrédités[16], elle a attiré l'attention sur la possibilité que cette dérive puisse générer de la variation cryptique de telle façon que, bien qu'elle soit neutre à la fonction actuelle, elle puisse affecter la sélection pour de nouvelles fonctions (évolvabilité)[17].
Par définition, tous les gènes au sein d'un réseau neutre possèdent une fonction équivalente ; cependant, certains peuvent montrer des promiscuités enzymatiques pouvant servir de points de départ à une évolution adaptative vers de nouvelles fonctions[18] - [19]. En termes d'espace de séquence, les théories actuelles prédisent que si les réseaux neutres pour deux activités différentes se chevauchent, une population évoluant de façon neutre peut se disperser vers des régions de la première activité du réseau lui permettant d'accéder à la deuxième activité[20]. Cela serait le cas seulement si la distance entre les activités est plus petite que la distance qu'une population évoluant de façon neutre peut couvrir. Le degré d'inter-pénétration des deux réseaux déterminera à quel point les variations sur les promiscuités enzymatiques sont cryptiques dans l'espace de séquence[21].
Cadre mathématique
Le fait que les mutations neutres soient probablement généralisées a été proposé par Freese et Yoshida en 1965[22]. Plus tard, Motoo Kimura a développé une théorie neutraliste de l'évolution en 1968[23], supportée par King et Jukes qui ont proposé indépendamment une théorie similaire en 1969[24]. Kimura a calculé le taux de substitutions nucléotidiques dans une population (soit le temps moyen nécessaire au remplacement d'une paire de bases au sein d'un génome) et a trouvé qu'il était de l'ordre de 1,8 année. Un taux aussi élevé ne serait toléré par aucune population mammalienne selon la formule de Haldane. En conséquence, il a conclu que, chez les mammifères, les mutations de substitutions nucléotidiques neutres (ou quasi-neutres) dans l'ADN doivent être dominantes. Il a calculé que de telles mutations ont lieu à un rythme d'environ 0-5 par année et par gamète.
Dans les années suivantes, un nouveau paradigme a émergé, qui place l'ARN comme molécule précurseur de l'ADN dans l'histoire de la vie. Un principe moléculaire primordial a été mis en avant dès 1968 par Crick[25], et a amené à ce que l'on appelle aujourd'hui l'hypothèse du monde à ARN[26]. L'ADN se trouve, de manière prédominante, sous forme de double hélice entièrement appariée en bases, alors que l'ARN biologique est simple brin et montre souvent des interactions complexes entre bases appariées. Cela est dû à sa capacité accrue à former des liaisons hydrogène, un fait qui découle de l'existence d'un groupe hydroxyle supplémentaire au sein du ribose.
Dans les années 1970, Stein et Waterman ont jeté les bases de la combinatoire des structures secondaires d'ARN[27]. Waterman a donné la première description théorique des structures secondaires d'ARN et les propriétés qui y sont associées, et les a utilisées pour produire un algorithme de repliement à énergie libre minimum (minimum free energy ou MFE en anglais) efficace[28]. Une structure secondaire d'ARN peut être vue comme un diagramme à N sommets étiquetés avec ses paires de bases de Watson & Crick représentées comme des arcs non croisés dans le demi-plan supérieur. Ainsi, une structure secondaire est un "échafaudage" ayant beaucoup de séquences compatibles avec ses contraintes impliquant un appariement de bases. Plus tard, Smith et Waterman ont développé un algorithme qui a pu réaliser des alignements locaux de séquences[29]. Nussinov a donné un autre algorithme de prédiction de la structure secondaire de l'ARN[30], décrivant un problème de repliement sur un alphabet à deux lettres comme un problème d'optimisation de graphe planaire où la quantité à maximiser est le nombre d'appariements dans la chaîne de séquence.
En 1980, Howell et ses collaborateurs ont calculé une fonction de génération de tous les repliements d'une séquence[31], alors que Sankoff en 1985 a décrit des algorithmes d'alignement de séquences finies, la prédiction de structures secondaires d'ARN (repliement), et la reconstruction de proto-séquences dans un arbre phylogénétique[32]. Plus tard, en 1986, Waterman et Temple ont produit un algorithme de programmation dynamique à temps polynomial pour prédire la structure secondaire générale de l'ARN[33], alors qu'en 1990, McCaskill a présenté un algorithme programmation dynamique à temps polynomial pour calculer la fonction de partition d'équilibre complet d'une structure secondaire d'ARN[34].
Zuker a mis en œuvre des algorithmes pour implémenter des algorithmes de calcul des MFE de structures secondaires de l'ARN[35] sur la base des travaux de Nussinov et al.[30], Smith et Waterman[29], et Studnicka et al.[36] Plus tard, Hofacker et ses collaborateurs en 1994[37] ont présenté le package ViennaRNA, un progiciel intégrant la MFE de repliement et le calcul de la fonction de partition, ainsi que des probabilités d'appariement de bases.
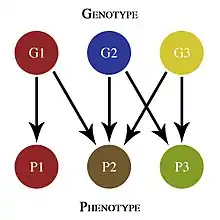
En 1994, Schuster et Fontana ont déplacé l'attention vers la séquence pour structurer les cartes génotype-phénotype. Ils ont utilisé un algorithme de repliement inverse, pour produire des preuves informatiques que les séquences d'ARN partageant la même structure sont distribuées au hasard dans l'espace de séquence. Ils ont observé que des structures communes peuvent être atteintes à partir d'une séquence aléatoire par seulement quelques mutations. Ces deux faits les amènent à conclure que l'espace de séquence semblait être percolé par des réseaux neutres de mutants voisins plus proches qui se replient vers la même structure[38].
En 1997, Stadler et Schuster ont jeté les bases mathématiques pour l'étude et la modélisation de réseaux neutres de structures secondaires d'ARN. En utilisant un modèle de graphe aléatoire, ils ont prouvé l'existence d'une valeur-seuil pour la connectivité de sous-graphes aléatoires dans un espace de configuration, paramétré par λ, la fraction des voisins neutres. Ils ont montré que les réseaux sont connectés et percolent l'espace de la séquence si la fraction des voisins proches neutres dépasse λ* (valeur-seuil). En-dessous de ce seuil, les réseaux sont partitionnés en un "composant géant" plus grand et plusieurs autres, plus petits. Les principaux résultats de cette analyse concernaient les fonctions de seuil pour la densité et la connectivité pour les réseaux neutres ainsi que la conjecture de l'espace de forme de Schuster[38] - [39] - [40].
Voir aussi
Notes
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Neutral network (evolution) » (voir la liste des auteurs).
- Schéma permettant de visualiser la relation entre des génotypes et le succès reproductif, avec la fitness comme axe vertical du paysage.
- Méthode de représentation de toutes les séquences possibles (protéine, gène ou génome) ; l'espace de séquence a une dimension par acide aminé ou nucléotide dans la séquence, menant à des espaces hautement dimensionnels.
Articles connexes
Références
- E. van Nimwegen, J. P. Crutchfield et M. Huynen, « Neutral evolution of mutational robustness », Proceedings of the National Academy of Sciences of the United States of America, vol. 96, no 17, , p. 9716–9720 (ISSN 0027-8424, PMID 10449760, lire en ligne, consulté le )
- Darin M. Taverna et Richard A. Goldstein, « Why are proteins so robust to site mutations? », Journal of Molecular Biology, vol. 315, no 3, , p. 479–484 (ISSN 0022-2836, PMID 11786027, DOI 10.1006/jmbi.2001.5226, lire en ligne, consulté le )
- Nobuhiko Tokuriki et Dan S. Tawfik, « Stability effects of mutations and protein evolvability », Current Opinion in Structural Biology, vol. 19, no 5, , p. 596–604 (ISSN 1879-033X, PMID 19765975, DOI 10.1016/j.sbi.2009.08.003, lire en ligne, consulté le )
- Leonid Meyerguz, Jon Kleinberg et Ron Elber, « The network of sequence flow between protein structures », Proceedings of the National Academy of Sciences of the United States of America, vol. 104, no 28, , p. 11627–11632 (ISSN 0027-8424, PMID 17596339, PMCID PMC1913895, DOI 10.1073/pnas.0701393104, lire en ligne, consulté le )
- Martin Karplus, « Behind the folding funnel diagram », Nature Chemical Biology, vol. 7, no 7, , p. 401–404 (ISSN 1552-4469, PMID 21685880, DOI 10.1038/nchembio.565, lire en ligne, consulté le )
- Elodie Monsellier et Fabrizio Chiti, « Prevention of amyloid-like aggregation as a driving force of protein evolution », EMBO reports, vol. 8, no 8, , p. 737–742 (ISSN 1469-221X, PMID 17668004, PMCID PMC1978086, DOI 10.1038/sj.embor.7401034, lire en ligne, consulté le )
- Jane Shelby Richardson et David C. Richardson, « Natural beta-sheet proteins use negative design to avoid edge-to-edge aggregation », Proceedings of the National Academy of Sciences of the United States of America, vol. 99, no 5, , p. 2754–2759 (ISSN 0027-8424, PMID 11880627, DOI 10.1073/pnas.052706099, lire en ligne, consulté le )
- Manuel M. Müller, Jane R. Allison, Narupat Hongdilokkul et Laurent Gaillon, « Directed evolution of a model primordial enzyme provides insights into the development of the genetic code », PLoS genetics, vol. 9, no 1, , e1003187 (ISSN 1553-7404, PMID 23300488, PMCID PMC3536711, DOI 10.1371/journal.pgen.1003187, lire en ligne, consulté le )
- Ryan T. Hietpas, Jeffrey D. Jensen et Daniel N. A. Bolon, « Experimental illumination of a fitness landscape », Proceedings of the National Academy of Sciences of the United States of America, vol. 108, no 19, , p. 7896–7901 (ISSN 1091-6490, PMID 21464309, PMCID PMC3093508, DOI 10.1073/pnas.1016024108, lire en ligne, consulté le )
- (en) Motoo Kimura, The Neutral Theory of Molecular Evolution, Cambridge University Press, , 367 p. (ISBN 978-0-521-31793-1, lire en ligne)
- M. Kimura, « Evolutionary rate at the molecular level », Nature, vol. 217, no 5129, , p. 624–626 (ISSN 0028-0836, PMID 5637732, lire en ligne, consulté le )
- S. R. Proulx et F. R. Adler, « The standard of neutrality: still flapping in the breeze? », Journal of Evolutionary Biology, vol. 23, no 7, , p. 1339–1350 (ISSN 1420-9101, PMID 20492093, DOI 10.1111/j.1420-9101.2010.02006.x, lire en ligne, consulté le )
- Jesse D Bloom, Zhongyi Lu, David Chen et Alpan Raval, « Evolution favors protein mutational robustness in sufficiently large populations », BMC Biology, vol. 5, , p. 29 (ISSN 1741-7007, PMID 17640347, PMCID PMC1995189, DOI 10.1186/1741-7007-5-29, lire en ligne, consulté le )
- Shimon Bershtein, Korina Goldin et Dan S. Tawfik, « Intense neutral drifts yield robust and evolvable consensus proteins », Journal of Molecular Biology, vol. 379, no 5, , p. 1029–1044 (ISSN 1089-8638, PMID 18495157, DOI 10.1016/j.jmb.2008.04.024, lire en ligne, consulté le )
- (en) Sewel Wright, The roles of mutation, inbreeding, crossbreeding and selection in evolution, University of Chicago, Chicago, Illinois, , p. 356-366
- Jerry A. Coyne, Nicholas H. Barton et Michael Turelli, « Perspective: A Critique of Sewall Wright's Shifting Balance Theory of Evolution », Evolution, vol. 51, no 3, , p. 643–671 (DOI 10.2307/2411143, lire en ligne, consulté le )
- E. K. Davies, A. D. Peters et P. D. Keightley, « High frequency of cryptic deleterious mutations in Caenorhabditis elegans », Science (New York, N.Y.), vol. 285, no 5434, , p. 1748–1751 (ISSN 0036-8075, PMID 10481013, lire en ligne, consulté le )
- Joanna Masel, « Cryptic genetic variation is enriched for potential adaptations », Genetics, vol. 172, no 3, , p. 1985–1991 (ISSN 0016-6731, PMID 16387877, PMCID PMC1456269, DOI 10.1534/genetics.105.051649, lire en ligne, consulté le )
- (en) Eric J. Hayden, Evandro Ferrada et Andreas Wagner, « Cryptic genetic variation promotes rapid evolutionary adaptation in an RNA enzyme », Nature, vol. 474, no 7349, , p. 92–95 (ISSN 0028-0836, DOI 10.1038/nature10083, lire en ligne, consulté le )
- Erich Bornberg-Bauer, Ann-Kathrin Huylmans et Tobias Sikosek, « How do new proteins arise? », Current Opinion in Structural Biology, nucleic acids / Sequences and topology, vol. 20, no 3, , p. 390–396 (DOI 10.1016/j.sbi.2010.02.005, lire en ligne, consulté le )
- (en) Andreas Wagner, The Origins of Evolutionary Innovations : A Theory of Transformative Change in Living Systems, OUP Oxford, , 264 p. (ISBN 978-0-19-162128-4, lire en ligne)
- (en) E. Freese et A. Yoshida, The role of mutations in evolution, Academic, New York, V. Bryson and H. J. Vogel eds., , p. 341-355
- (en) M. Kimura, « Evolutionary Rate at the Molecular Level », Nature, vol. 217, , p. 624-626 (lire en ligne)
- (en) J.L. King et T. H. Jukes, « Non-Darwinian Evolution », Science, vol. 164, , p. 788-797 (lire en ligne)
- F. H. Crick, « The origin of the genetic code », Journal of Molecular Biology, vol. 38, no 3, , p. 367–379 (ISSN 0022-2836, PMID 4887876, lire en ligne, consulté le )
- Michael P. Robertson et Gerald F. Joyce, « The origins of the RNA world », Cold Spring Harbor Perspectives in Biology, vol. 4, no 5, (ISSN 1943-0264, PMID 20739415, PMCID PMC3331698, DOI 10.1101/cshperspect.a003608, lire en ligne, consulté le )
- P. R. Stein et M. S. Waterman, « On some new sequences generalizing the Catalan and Motzkin numbers », Discrete Mathematics, vol. 26, no 3, , p. 261–272 (DOI 10.1016/0012-365X(79)90033-5, lire en ligne, consulté le )
- (en) M. S. Waterman, Secondary structure of single : stranded nucleic acids, Adv. Math.I (suppl.), , p. 167-212
- T. F. Smith et M. S. Waterman, « Identification of common molecular subsequences », Journal of Molecular Biology, vol. 147, no 1, , p. 195–197 (ISSN 0022-2836, PMID 7265238, lire en ligne, consulté le )
- R. Nussinov, G. Pieczenik, J. Griggs et D. Kleitman, « Algorithms for Loop Matchings », SIAM Journal on Applied Mathematics, vol. 35, no 1, , p. 68–82 (ISSN 0036-1399, DOI 10.1137/0135006, lire en ligne, consulté le )
- J. Howell, T. Smith et M. Waterman, « Computation of Generating Functions for Biological Molecules », SIAM Journal on Applied Mathematics, vol. 39, no 1, , p. 119–133 (ISSN 0036-1399, DOI 10.1137/0139010, lire en ligne, consulté le )
- D. Sankoff, « Simultaneous Solution of the RNA Folding, Alignment and Protosequence Problems », SIAM Journal on Applied Mathematics, vol. 45, no 5, , p. 810–825 (ISSN 0036-1399, DOI 10.1137/0145048, lire en ligne, consulté le )
- Michael S Waterman et Temple F Smith, « Rapid dynamic programming algorithms for RNA secondary structure », Advances in Applied Mathematics, vol. 7, no 4, , p. 455–464 (DOI 10.1016/0196-8858(86)90025-4, lire en ligne, consulté le )
- J. S. McCaskill, « The equilibrium partition function and base pair binding probabilities for RNA secondary structure », Biopolymers, vol. 29, nos 6-7, , p. 1105–1119 (ISSN 0006-3525, PMID 1695107, DOI 10.1002/bip.360290621, lire en ligne, consulté le )
- Michael Zuker et Patrick Stiegler, « Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information », Nucleic Acids Research, vol. 9, no 1, , p. 133–148 (ISSN 0305-1048, DOI 10.1093/nar/9.1.133, lire en ligne, consulté le )
- (en) Gary M. Studnicka, Georgia M. Rahn, Ian W. Cummings et Winston A. Salser, « Computer method for predicting the secondary structure of single-stranded RNA », Nucleic Acids Research, vol. 5, no 9, , p. 3365–3388 (ISSN 0305-1048, DOI 10.1093/nar/5.9.3365, lire en ligne, consulté le )
- (en) I. L. Hofacker, W. Fontana, P. F. Stadler et L. S. Bonhoeffer, « Fast folding and comparison of RNA secondary structures », Monatshefte für Chemie / Chemical Monthly, vol. 125, no 2, , p. 167–188 (ISSN 0026-9247 et 1434-4475, DOI 10.1007/BF00818163, lire en ligne, consulté le )
- P. Schuster, W. Fontana, P. F. Stadler et I. L. Hofacker, « From sequences to shapes and back: a case study in RNA secondary structures », Proceedings. Biological Sciences, vol. 255, no 1344, , p. 279–284 (ISSN 0962-8452, PMID 7517565, DOI 10.1098/rspb.1994.0040, lire en ligne, consulté le )
- (en) Christian Michael Reidys, Neutral Networks of RNA Secondary Structures, Lippstadt, (lire en ligne)
- Ivo L. Hofacker, Peter Schuster et Peter F. Stadler, « Combinatorics of RNA secondary structures », Discrete Applied Mathematics, computational Molecular Biology DAM - CMB Series, vol. 88, no 1, , p. 207–237 (DOI 10.1016/S0166-218X(98)00073-0, lire en ligne, consulté le )