Quaternions et rotation dans l'espace

Les quaternions unitaires représentent l'espace mathématique des rotations en trois dimensions (autour d’un axe passant par l’origine) de façon relativement simple. On peut comprendre la correspondance entre les rotations et les quaternions en commençant par se faire une idée intuitive de l'espace des rotations lui-même (une présentation plus rigoureuse interpréterait l’ensemble des rotations comme un groupe de Lie, et l’espace associé comme une 3-variété, mais ce niveau d’abstraction est inutile pour les applications pratiques discutées dans cet article).

Deux rotations d'angles différents et d'axes différents dans l'espace des rotations. La norme du vecteur est liée à l'amplitude de la rotation.

Chaque rotation en trois dimensions consiste à tourner d'un certain angle autour d'un certain axe. Quand l'angle est nul, l'axe n'a pas d'importance, de telle façon qu'une rotation de zéro degré est un simple point dans l'espace des rotations (c'est la rotation identité). Pour un angle petit mais non nul, l'ensemble des rotations possibles est une petite sphère entourant la rotation identité, où chaque point de la sphère représente un axe pointant dans une direction particulière (comparez avec la sphère céleste). Des rotations d'angles de plus en plus grands s'éloignent progressivement de la rotation identité, et nous pouvons nous les représenter comme des sphères concentriques de rayons croissants. En conséquence, au voisinage de la rotation identité, l'espace abstrait des rotations ressemble à l'espace ordinaire en trois dimensions (qui peut également être vu comme un point central entouré de sphères de différents rayons). La ressemblance s'arrête là : lorsque l'angle de rotation dépasse 180°, les rotations suivant les différents axes cessent de diverger et commencent à nouveau à se ressembler, pour finir par devenir identiques (et égales à la rotation identité) lorsque l'angle atteint 360°.

L'hypersphère des rotations pour les rotations d'axes horizontaux (axes compris dans le plan xy).

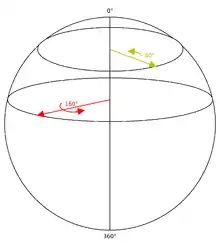
On constate un phénomène analogue à la surface d'une sphère. Si nous nous plaçons au pôle Nord et traçons à partir de là des lignes droites (en fait, des méridiens) dans plusieurs directions, elles divergeront puis convergeront à nouveau au pôle Sud. Des cercles concentriques de rayon croissant dessinés autour du pôle Nord (des parallèles) finiront par s'effondrer en un point au pôle Sud une fois que l'on a parcouru la distance entre les pôles. On peut assimiler les différentes directions à partir du pôle (c'est-à-dire les différents méridiens) aux différents axes de rotations et les différentes distances au pôle Nord aux différents angles : on a ainsi une analogie de l'espace des rotations. Mais la surface de la sphère est en deux dimensions alors que les axes de rotation utilisent déjà trois dimensions. L'espace des rotations est donc modélisé par une sphère de dimension 3 dans un espace à 4 dimensions (une hypersphère). Nous pouvons penser à la sphère ordinaire comme à une section de l'hypersphère, de la même façon qu'un cercle est une section de sphère. On peut prendre la section pour représenter, par exemple, uniquement les rotations d'axes dans le plan xy (voir illustration ci-contre). On remarque que l'angle de la rotation est deux fois la différence de latitude avec le pôle Nord : en effet, les points de l'équateur représentent des rotations de 180°, pas de 90°, et le pôle Sud représente la rotation identité de 360°, et pas le demi-tour de 180°.

Le pôle Nord et le pôle Sud représentent la même rotation, et en fait cela s'applique à n'importe quelle paire de points aux antipodes l'un de l'autre : si un point correspond à une rotation d'angle ${\displaystyle \alpha }$ autour de l'axe dirigé par le vecteur ${\displaystyle {\vec {v}}}$, l'autre point correspond à une rotation d'angle ${\displaystyle 360^{\circ }-\alpha }$ autour de l'axe dirigé par le vecteur ${\displaystyle -{\vec {v}}}$. En fait, l'espace des rotations n'est pas l'hypersphère elle-même, mais l'hypersphère où l'on identifie les points aux antipodes l'un de l'autre. Mais dans un but de simplification, nous pouvons penser aux rotations comme à des points de la sphère en dimension 4, même si la moitié de ces points est redondante (revêtement double).

Nous pouvons paramétrer la surface d'une sphère à l'aide de deux coordonnées, comme la latitude et la longitude. Mais la latitude et la longitude se comportent mal (sont dégénérés) aux pôles Nord et Sud, alors que les pôles ne sont pas différents par nature des autres points de la sphère. Aux pôles Nord et Sud (de latitudes +90° et -90°), la longitude perd son sens.

On peut montrer qu'aucun système de coordonnées à deux paramètres ne peut éviter cette dégénérescence (c'est le théorème de la boule chevelue). Nous pouvons éviter de tels problèmes en plongeant la sphère dans l'espace à trois dimensions et en la paramétrant au moyen de trois coordonnées cartésiennes (ici w, x et y), en plaçant le pôle Nord à (w, x, y) = (1, 0, 0), le pôle Sud à (w, x, y) = (−1, 0, 0) et l'équateur sera le cercle d'équations w = 0 et x² + y² = 1. Les points de la sphère satisfont la contrainte w² + x² + y² = 1, donc nous avons toujours deux degrés de liberté, bien que l'on ait trois coordonnées. Un point (w, x, y) de la sphère représente une rotation de l'espace ordinaire autour de l'axe horizontal dirigé par le vecteur ${\displaystyle {\begin{pmatrix}x\\y\\0\end{pmatrix}}}$ et d'angle ${\displaystyle \alpha =2\arccos w=2\arcsin {\sqrt {x^{2}+y^{2}}}}$.

De la même façon, l'hypersphère décrivant l'espace des rotations dans l'espace en trois dimensions peut être paramétrée au moyen de trois angles (angles d'Euler), mais tout paramétrage de ce type dégénère en certains points de l'hypersphère, ce qui conduit au problème du blocage de cardan. Nous pouvons éviter cela en utilisant quatre coordonnées euclidennes w, x, y et z, avec w² + x² + y² + z² = 1. Le point de coordonnées (w, x, y, z) représente une rotation autour de l'axe dirigé par le vecteur ${\displaystyle {\begin{pmatrix}x\\y\\z\end{pmatrix}}}$ et d'angle ${\displaystyle \alpha =2\arccos w=2\arcsin {\sqrt {x^{2}+y^{2}+z^{2}}}.}$

On peut définir les nombres complexes en introduisant un symbole abstrait i qui se conforme aux règles usuelles de l'algèbre et qui en plus obéit à la règle i² = −1. Cela suffit à reproduire toutes les règles de calcul des nombres complexes, par exemple ${\displaystyle (a+b\mathbf {i} )(c+d\mathbf {i} )=ac+ad\mathbf {i} +b\mathbf {i} c+b\mathbf {i} d\mathbf {i} =ac+ad\mathbf {i} +bc\mathbf {i} +bd\mathbf {i} ^{2}=(ac-bd)+(bc+ad)\mathbf {i} }$.

De la même façon, les quaternions peuvent être définis en introduisant des symboles abstraits i, j et k qui satisfont aux règles i² = j² = k² = ijk = −1 et les règles algébriques usuelles sauf la commutativité de la multiplication (un exemple familier de multiplication non commutative est la multiplication des matrices). L'ensemble des règles de calcul découle de ces définitions ; par exemple, on peut montrer que ${\displaystyle (a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} )(e+f\mathbf {i} +g\mathbf {j} +h\mathbf {k} )=(ae-bf-cg-dh)+(af+be+ch-dg)\mathbf {i} +(ag+ce+df-bh)\mathbf {j} +(ah+de+bg-cf)\mathbf {k} }$.

La partie imaginaire ${\displaystyle b\mathbf {i} +c\mathbf {j} +d\mathbf {k} }$ d'un quaternion se comporte comme un vecteur ${\displaystyle {\vec {v}}={\begin{pmatrix}b\\c\\d\end{pmatrix}}}$ d'un espace vectoriel à trois dimensions et la partie réelle a comme un scalaire de ${\displaystyle \mathbb {R} }$. Quand les quaternions sont utilisés en géométrie, il est pratique de les définir comme un scalaire plus un vecteur: ${\displaystyle a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =a+{\vec {v}}}$.

Ceux qui ont étudié les vecteurs à un niveau élémentaire pourraient trouver étrange d'additionner un nombre à un vecteur, car ce sont des objets de natures très différentes, ou de multiplier deux vecteurs entre eux, car cette opération n'est d'habitude pas définie. Néanmoins, si l'on se souvient qu'il ne s'agit là que d'une notation pour les parties réelles et imaginaires d'un quaternion, cela devient plus légitime.

Nous pouvons exprimer la multiplication de quaternions (produit de Hamilton) dans le langage moderne du produit vectoriel et du produit scalaire de vecteurs (qui ont en fait été inspirés au début par les quaternions). À la place des règles i² = j² = k² = ijk = −1, nous avons la règle de multiplication de deux vecteurs ${\displaystyle {\vec {v}}{\vec {w}}=-{\vec {v}}\cdot {\vec {w}}+{\vec {v}}\wedge {\vec {w}}}$, où :

• ${\displaystyle {\vec {v}}{\vec {w}}}$ est le quaternion résultant,
• ${\displaystyle {\vec {v}}\wedge {\vec {w}}}$ est le produit vectoriel (un vecteur),
• ${\displaystyle {\vec {v}}\cdot {\vec {w}}}$ est le produit scalaire (un nombre).

La multiplication de vecteurs n'est pas commutative (à cause du produit vectoriel), alors que la multiplication entre scalaires et celle entre un scalaire et un vecteur sont commutatives. Il découle de manière immédiate de ces règles que ${\displaystyle (s+{\vec {v}})(t+{\vec {w}})=(st-{\vec {v}}\cdot {\vec {w}})+(s{\vec {w}}+t{\vec {v}}+{\vec {v}}\wedge {\vec {w}})}$.

L'inverse (à gauche et à droite) d'un quaternion non nul est ${\displaystyle (s+{\vec {v}})^{-1}={\frac {s-{\vec {v}}}{s^{2}+|{\vec {v}}|^{2}}}}$, comme cela peut être vérifié par calcul direct.

Soient (w, x, y, z) les coordonnées d'une rotation, comme décrit précédemment. Définissons le quaternion : ${\displaystyle q=w+x\mathbf {i} +y\mathbf {j} +z\mathbf {k} =w+{\begin{pmatrix}x\\y\\z\end{pmatrix}}=\cos(\alpha /2)+{\vec {u}}\sin(\alpha /2)}$ où ${\displaystyle {\vec {u}}}$ est un vecteur unitaire. Soit également ${\displaystyle {\vec {v}}}$ un vecteur ordinaire de l'espace en 3 dimensions, considéré comme un quaternion avec une coordonnée réelle nulle. On peut alors montrer (voir section suivante) que le produit de quaternions

${\displaystyle q{\vec {v}}q^{-1}}$

renvoie le vecteur ${\displaystyle {\vec {v}}}$ tourné d'un angle ${\displaystyle \alpha }$ autour de l'axe dirigé par ${\displaystyle {\vec {u}}}$. La rotation se fait dans le sens des aiguilles d'une montre si notre ligne de vue pointe dans la même direction que ${\displaystyle {\vec {u}}}$. Cette opération est connue comme la conjugaison par q.

Il s'ensuit que la multiplication de quaternions correspond à la composition de rotations, car si p et q sont des quaternions représentant des rotations, alors la rotation (conjugaison) par pq est

${\displaystyle pq{\vec {v}}(pq)^{-1}=pq{\vec {v}}q^{-1}p^{-1}=p(q{\vec {v}}q^{-1})p^{-1}}$,

ce qui revient à tourner (conjuguer) par q, puis par p.

Le quaternion inverse d'une rotation correspond à la rotation inverse, car ${\displaystyle q^{-1}(q{\vec {v}}q^{-1})q={\vec {v}}}$. Le carré d'un quaternion correspond à la rotation de deux fois le même angle autour du même axe. Plus généralement, qⁿ correspond à une rotation de n fois l'angle autour du même axe que q. Cela peut être étendu à un réel arbitraire n, ce qui permet de calculer des rotations intermédiaires de façon fluide entre des rotations de l'espace, c'est l'interpolation linéaire sphérique (en).

Soit ${\displaystyle {\vec {u}}}$ un vecteur unitaire (l'axe de rotation) et soit ${\displaystyle q=\cos {\frac {\alpha }{2}}+{\vec {u}}\sin {\frac {\alpha }{2}}}$.

Notre but est de montrer que :

${\displaystyle {\vec {v'}}=q{\vec {v}}q^{-1}=\left(\cos {\frac {\alpha }{2}}+{\vec {u}}\sin {\frac {\alpha }{2}}\right)\,{\vec {v}}\,\left(\cos {\frac {\alpha }{2}}-{\vec {u}}\sin {\frac {\alpha }{2}}\right)}$

renvoie le vecteur ${\displaystyle {\vec {v}}}$ tourné d'un angle ${\displaystyle \alpha }$ autour de l'axe dirigé par ${\displaystyle {\vec {u}}}$.

En développant, on obtient en effet :

${\displaystyle {\begin{array}{lll}{\vec {v'}}&=&{\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+({\vec {u}}{\vec {v}}-{\vec {v}}{\vec {u}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-{\vec {u}}{\vec {v}}{\vec {u}}\sin ^{2}{\frac {\alpha }{2}}\\&=&{\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2({\vec {u}}\wedge {\vec {v}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-({\vec {v}}({\vec {u}}\cdot {\vec {u}})-2{\vec {u}}({\vec {u}}\cdot {\vec {v}}))\sin ^{2}{\frac {\alpha }{2}}\\&=&{\vec {v}}(\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\alpha }{2}})+({\vec {u}}\wedge {\vec {v}})(2\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}})+{\vec {u}}({\vec {u}}\cdot {\vec {v}})(2\sin ^{2}{\frac {\alpha }{2}})\\&=&{\vec {v}}\cos \alpha +({\vec {u}}\wedge {\vec {v}})\sin \alpha +{\vec {u}}({\vec {u}}\cdot {\vec {v}})(1-\cos \alpha )\\&=&({\vec {v}}-{\vec {u}}({\vec {u}}\cdot {\vec {v}}))\cos \alpha +({\vec {u}}\wedge {\vec {v}})\sin \alpha +{\vec {u}}({\vec {u}}\cdot {\vec {v}})\\&=&{\vec {v}}_{\bot }\cos \alpha +({\vec {u}}\wedge {\vec {v}})\sin \alpha +{\vec {v}}_{\|}\end{array}}}$

où ${\displaystyle {\vec {v}}_{\bot }}$ et ${\displaystyle {\vec {v}}_{\|}}$ sont les composantes de ${\displaystyle {\vec {v}}}$ respectivement orthogonale et colinéaire à ${\displaystyle {\vec {u}}}$. C'est là la formule d'Olinde Rodrigues qui donne la rotation d'angle ${\displaystyle \alpha }$ autour de l'axe dirigé par ${\displaystyle {\vec {u}}}$.

Une rotation de 120° autour de la première diagonale permute i, j et k circulairement.

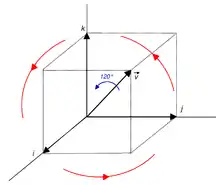
Considérons la rotation f autour de l'axe dirigé par ${\displaystyle {\vec {v}}=\mathbf {i} +\mathbf {j} +\mathbf {k} }$ et d'angle 120°, c'est-à-dire ^2π/₃ radians.

${\displaystyle \alpha ={\frac {2\pi }{3}}}$.

La norme de ${\displaystyle {\vec {v}}}$ est √3, le demi-angle est ^π/₃ (60°), le cosinus de ce demi-angle est ¹/₂, (cos 60° = 0,5) et son sinus est ^√3/₂, (sin 60° ≈ 0,866). Nous devons donc conjuguer avec le quaternion unitaire :

${\displaystyle {\begin{array}{lll}q&=&\cos {\frac {\alpha }{2}}+\sin {\frac {\alpha }{2}}\cdot {\frac {1}{\|{\vec {v}}\|}}{\vec {v}}\\&=&\cos {\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\cdot {\frac {1}{\sqrt {3}}}{\vec {v}}\\&=&{\frac {1}{2}}+{\frac {\sqrt {3}}{2}}\cdot {\frac {1}{\sqrt {3}}}{\vec {v}}\\&=&{\frac {1}{2}}+{\frac {\sqrt {3}}{2}}\cdot {\frac {\mathbf {i} +\mathbf {j} +\mathbf {k} }{\sqrt {3}}}\\&=&{\frac {1+\mathbf {i} +\mathbf {j} +\mathbf {k} }{2}}\end{array}}}$

Si f est la fonction de rotation,

${\displaystyle f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )=q(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )q^{-1}}$

On peut prouver que l'on obtient l'inverse d'un quaternion unitaire simplement en changeant le signe de ses coordonnées imaginaires. En conséquence,

${\displaystyle q^{-1}={\frac {1-\mathbf {i} -\mathbf {j} -\mathbf {k} }{2}}}$

et

${\displaystyle f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )={\frac {1+\mathbf {i} +\mathbf {j} +\mathbf {k} }{2}}(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} ){\frac {1-\mathbf {i} -\mathbf {j} -\mathbf {k} }{2}}}$

En appliquant les règles ordinaires de calcul avec les quaternions, on obtient

${\displaystyle f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )=c\mathbf {i} +a\mathbf {j} +b\mathbf {k} }$.

Comme on s'y attendait, la rotation revient à tenir un cube par un de ses sommets, puis à le faire tourner de 120° selon la diagonale la plus longue qui passe par ce point. On observe comment les trois axes subissent une permutation circulaire.

La multiplication des quaternions est non commutative. Comme multiplier des quaternions unitaires revient à composer les rotations dans l'espace à trois dimensions, on peut rendre cette propriété intuitive grâce au fait que les rotations en trois dimensions ne commutent pas en général.

Un simple exercice consistant à appliquer deux rotations successives à un objet asymétrique (par exemple un livre) peut l'expliquer. D'abord, tournez un livre de 90 degrés dans le sens des aiguilles d'une montre autour de l'axe des Z. Ensuite, basculez-le de 180 degrés autour de l'axe des X et mémorisez le résultat. Revenez à la position de départ, de manière à pouvoir lire à nouveau le titre du livre, et appliquez les rotations en ordre inverse. Comparez le résultat au résultat précédent. Cela montre que, en général, la composition de deux rotations différentes autour de deux axes distincts de l'espace ne commute pas.

Il convient de remarquer que les quaternions, comme n'importe quelle rotation ou application linéaire, ne sont pas "orientés" (il n'y a pas de sens direct ou indirect). L'orientation d'un système de coordonnées provient de l'interprétation des nombres dans l'espace physique. Quelle que soit la convention d'orientation que l'on choisisse, faire tourner le vecteur X de 90 degrés autour du vecteur Z renverra le vecteur Y — la théorie et les calculs donnent le même résultat.

La représentation d'une rotation sous la forme d'un quaternion (4 nombres) est plus compacte que la représentation en tant que matrice orthogonale (9 nombres). De plus, pour un axe et un angle donné, on peut facilement construire le quaternion correspondant, et réciproquement, pour un quaternion donné, on peut facilement extraire l'axe et l'angle. Toutes ces opérations sont beaucoup plus difficiles avec des matrices ou des angles d'Euler.

Dans les jeux vidéo et dans d'autres applications, on a souvent besoin de « rotations fluides », c'est-à-dire que la scène représentée doit tourner harmonieusement et pas d'un seul coup. On peut obtenir ce résultat en choisissant une courbe comme celle de l'interpolation linéaire sphérique dans l'espace des quaternions, avec une extrémité qui est la transformation identique 1 (ou correspondant à une autre rotation initiale) et l'autre extrémité correspondant à la rotation finale désirée. C'est plus difficile à faire avec d'autres représentations des rotations.

Quand on compose plusieurs rotations sur un ordinateur, les erreurs d'arrondi s'accumulent forcément. Un quaternion qui est légèrement erroné représente toujours une rotation après avoir été renormalisé ; une matrice qui est légèrement erronée ne sera plus orthogonale et sera difficile à convertir à nouveau en une matrice orthogonale qui convienne.

Les quaternions évitent également un phénomène appelé le blocage de cardan qui peut apparaître lorsque, par exemple dans des systèmes de rotations décrivant le roulis, le tangage et le lacet, le tangage est de 90° vers le haut ou le bas, de telle façon que le roulis et le lacet correspondent au même mouvement, et qu'un degré de liberté ait été perdu. Dans un système de navigation inertielle à base de cardans, par exemple, cela peut avoir des conséquences désastreuses si l'avion monte en flèche ou descend à pic.

La matrice orthogonale correspondant à une rotation au moyen du quaternion unitaire ${\displaystyle z=a+bi+cj+dk}$ (avec ${\displaystyle |z|=1}$) est donnée par

${\displaystyle {\begin{pmatrix}a^{2}+b^{2}-c^{2}-d^{2}&2bc-2ad&2ac+2bd\\2ad+2bc&a^{2}-b^{2}+c^{2}-d^{2}&2cd-2ab\\2bd-2ac&2ab+2cd&a^{2}-b^{2}-c^{2}+d^{2}\\\end{pmatrix}}.}$

Chercher le quaternion ${\displaystyle (q_{0}+q_{x}i+q_{y}j+q_{z}k)}$ correspondant à la matrice de rotation ${\displaystyle Q_{ij}}$ peut être instable numériquement si la trace (la somme des éléments de la diagonale de la matrice) de la matrice de rotation est nulle ou très petite. Une méthode robuste consiste à choisir l'élément de la diagonale ayant la valeur ${\displaystyle Q_{uu}}$ la plus grande en valeur absolue. Considérons

${\displaystyle r=\pm {\frac {1}{2}}{\sqrt {1+Q_{uu}+Q_{vv}+Q_{ww}}}}$

Cette écriture est légitime car l'expression sous la racine est positive. Si r est nul, cela équivaut à une trace égale à -1 (soit un angle de rotation de π). La rotation est une symétrie axiale et donc le quaternion a la forme suivante (0 , ${\displaystyle {\vec {u}}}$.x , ${\displaystyle {\vec {u}}}$.y , ${\displaystyle {\vec {u}}}$.z) avec ${\displaystyle {\vec {u}}}$ vecteur unitaire dirigeant l'axe de rotation. Sinon le quaternion peut alors être écrit sous la forme[3] :

${\displaystyle q_{0}=r}$

${\displaystyle q_{u}={\frac {1}{4r}}(Q_{wv}-Q_{vw})}$

${\displaystyle q_{v}={\frac {1}{4r}}(Q_{uw}-Q_{wu})}$

${\displaystyle q_{w}={\frac {1}{4r}}(Q_{vu}-Q_{uv})}$

Attention, il y a deux conventions pour les vecteurs : l'une suppose que les matrices de rotation sont multipliées par des vecteurs-ligne à gauche, l'autre par des vecteurs-colonne à droite ; les deux conventions conduisent à des matrices qui sont transposées l'une de l'autre. La matrice ci-dessus suppose que l'on utilise des vecteurs colonne à droite. Historiquement, la convention vecteur-colonne-à-droite provient des mathématiques et de la mécanique classique, alors que la convention vecteur-ligne-à-gauche provient de l'infographie, où il était plus facile de saisir des vecteurs-lignes aux débuts de la discipline.

La section ci-dessus a décrit comment récupérer un quaternion q à partir d'une matrice de rotation 3 × 3 Q. Supposons, néanmoins, que nous avons une matrice Q qui n'est pas celle d'une rotation pure, à cause d'erreurs d'arrondi, par exemple, et que nous souhaitions trouver le quaternion q qui représente Q le plus précisément possible. Dans ce cas, nous construisons une matrice 4 × 4 symétrique

${\displaystyle K={\frac {1}{3}}{\begin{bmatrix}Q_{xx}-Q_{yy}-Q_{zz}&Q_{yx}+Q_{xy}&Q_{zx}+Q_{xz}&Q_{yz}-Q_{zy}\\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{zx}-Q_{xz}\\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{xy}-Q_{yx}\\Q_{yz}-Q_{zy}&Q_{zx}-Q_{xz}&Q_{xy}-Q_{yx}&Q_{xx}+Q_{yy}+Q_{zz}\end{bmatrix}}}$

et nous cherchons le vecteur propre de coordonnées (x, y, z, w) correspondant à la plus grande valeur propre (cette valeur vaut 1 si et seulement si Q est une rotation pure). Le quaternion ainsi obtenu correspondra à la rotation la plus proche de la matrice Q de départ[4].

Cette section traite des implications en matière de performances de l'utilisation de quaternions par rapport à d'autres méthodes (axe et angle ou matrices de rotation) pour effectuer des rotations en 3D.

* Note : la représentation sous forme d'angle et d'axe peut être stockée dans 3 emplacements seulement en multipliant l'axe de rotation par l'angle de rotation ; néanmoins, avant de l'utiliser, il faut récupérer le vecteur unitaire et l'angle en renormalisant, ce qui coûte des opérations mathématiques supplémentaires.

Il y a trois techniques de base pour faire tourner un vecteur ${\displaystyle {\vec {v}}}$ :

1. Calculer le produit matriciel de la matrice de rotation 3 × 3 représentant la rotation R par la matrice colonne 3 × 1 représentant le vecteur ${\displaystyle {\vec {v}}}$. Cela nécessite 3 x (3 multiplications + 2 additions) = 9 multiplications et 6 additions, c'est la méthode la plus efficace pour faire tourner un vecteur.
2. Utiliser la formule de rotation avec des quaternions dite action par conjugaison ${\displaystyle {\vec {v}}_{\text{new}}=z{\vec {v}}z^{-1}}$. Calculer ce résultat revient à transformer le quaternion en une matrice de rotation R en utilisant la formule de conversion d'un quaternion en matrice orthogonale, puis à multiplier le résultat par la matrice-colonne représentant le vecteur. En procédant à une recherche de sous-expressions communes, l'algorithme se ramène à 21 multiplications et 18 additions. Une autre approche peut consister à convertir d'abord le quaternion dans la représentation sous forme d'axe et d'angle équivalente, puis à s'en servir pour faire tourner le vecteur. Néanmoins, c'est à la fois moins efficace et moins stable numériquement lorsque le quaternion est voisin de la rotation identité.
3. Convertir la représentation sous forme d'axe et d'angle en matrice de rotation R, puis multiplier par la matrice-colonne représentant le vecteur. La conversion coûte 14 multiplications, 2 appels de fonction (sin et cos) et 10 additions ou soustractions après recherche de sous-expressions communes, puis la rotation ajoute 9 multiplications et 6 additions pour un total de 21 multiplications, 16 additions ou soustractions et deux appels de fonctions trigonométriques.

Pseudo-code pour la rotation à l'aide de quaternions

Étant donné un quaternion z = a + bi + cj + dk (avec |z| = 1) et un vecteur ${\displaystyle {\vec {v}}}$ de coordonnées v1, v2 et v3, le code qui suit effectue une rotation. Notez l'utilisation de variables temporaires txx. Notez aussi l'optimisation des éléments de la diagonale de la matrice R : comme ${\displaystyle a^{2}+b^{2}+c^{2}+d^{2}=1}$, on réécrit l'élément en haut à gauche sous la forme ${\displaystyle a^{2}+b^{2}+c^{2}+d^{2}-2c^{2}-2d^{2}=1-2c^{2}-2d^{2}}$ ; les deux autres éléments de la diagonale peuvent être réécrits de même.

t2 =   a*b
t3 =   a*c
t4 =   a*d
t5 =  -b*b
t6 =   b*c
t7 =   b*d
t8 =  -c*c
t9 =   c*d
t10 = -d*d
v1new = 2*( (t8 + t10)*v1 + (t6 -  t4)*v2 + (t3 + t7)*v3 ) + v1
v2new = 2*( (t4 +  t6)*v1 + (t5 + t10)*v2 + (t9 - t2)*v3 ) + v2
v3new = 2*( (t7 -  t3)*v1 + (t2 +  t9)*v2 + (t5 + t8)*v3 ) + v3

Pseudo-code pour créer une matrice angle et axe

Étant donné un vecteur unitaire de coordonnées (v1, v2, v3) et un angle θ, la matrice de rotation peut être calculée avec :

t1 =  cos(theta)
t2 =  1 - t1
t3 =  v1*v1
t6 =  t2*v1
t7 =  t6*v2
t8 =  sin(theta)
t9 =  t8*v3
t11 = t6*v3
t12 = t8*v2
t15 = v2*v2
t19 = t2*v2*v3
t20 = t8*v1
t24 = v3*v3
R[1, 1] = t1 + t2*t3
R[1, 2] = t7 - t9
R[1, 3] = t11 + t12
R[2, 1] = t7 + t9
R[2, 2] = t1 + t2*t15
R[2, 3] = t19 - t20
R[3, 1] = t11 - t12
R[3, 2] = t19 + t20
R[3, 3] = t1 + t2*t24

• APL (langage)
• Quaternion
• Biquaternion
• Angles d'Euler
• Blocage de cardan
• Rotation dans l'espace
• Matrice de rotation
• Algèbre de Clifford
• Groupe Spin
• Revêtement

• (en) Shoemake, Ken. Quaternion tutorial
• (en) Hart, Francis, Kauffman. Quaternion demo
• (en) Dam, Koch, Lillholm. Quaternions, Interpolation and Animation
• (en) Byung-Uk Lee, Unit Quaternion Representation of Rotation
• (en) Ibanez, Luis, Quaternion Tutorial I
• (en) Ibanez, Luis, Quaternion Tutorial II
• (en) Leandra Vicci, Quaternions and Rotations in 3-Space: The Algebra and its Geometric Interpretation
• Un cours sur les quaternions et les rotations.
• Présentation mathématique des quaternions incluant une animation WebGL