Problème de Milne

Le problème du transfert radiatif (au sens large, incluant le transfert neutronique et de nombreuses autres particules élémentaires ou non) est décrit par l'équation de Boltzmann[N 1]. Il s'agit d'une équation intégro-différentielle linéaire portant sur la distribution angulaire du nombre de particules transportées ou de toute quantité relative à celui-ci (l'énergie par exemple, auquel cas on parle de luminance totale, c'est-à-dire intégrée sur tout le spectre électromagnétique). La résolution de ce problème est possible dans le cas d'un problème unidimensionnel plan, cylindrique ou sphérique dans le cas particulier d'une diffusion isotrope dans le milieu. Cette résolution a une origine historique, les travaux ayant été menés à une époque où le calcul numérique n'existait pas. Ils sont aujourd'hui utilisés comme benchmark pour tester des méthodes numériques.

L'équation de Boltzmann pour un milieu homogène stationnaire, unidimensionnel et semi-infini, sans émission ni absorption en volume, avec diffusion isotrope[N 2] s'écrit

${\displaystyle \mu {\frac {\mathrm {d} L(\tau ,\mu )}{\mathrm {d} \tau }}+L(\tau ,\mu )=\underbrace {{\frac {1}{2}}\int _{-1}^{1}L(\tau ,\mu )\mathrm {d} \mu } _{terme~source~S}}$

où

${\displaystyle L(\tau ,\mu )}$	luminance,
${\displaystyle \mu =\cos {\theta }}$	avec θ l'angle de propagation,
${\displaystyle \tau =\kappa _{t}x}$	épaisseur optique (ou profondeur optique),
${\displaystyle \kappa _{t}}$	coefficient d'extinction totale supposé constant.

On utilise également l'énergie volumique définie par

${\displaystyle E(\tau )={\frac {2\pi }{c}}\int _{-1}^{1}L(\tau ,\mu )\mathrm {d} \mu }$

où c est la vitesse de la lumière. À l'énergie on associe parfois une température radiative T_R qui est celle du corps noir produisant la même énergie rayonnée, définie par E = 4 σ T_R⁴ / c où σ est la constante de Stefan-Boltzmann. L'hypothèse κ^t constant implique la conservation du spectre dans le milieu, lequel est donc celui de la source. T_R n'est donc pas en général la température thermodynamique du milieu, laquelle ne joue aucun rôle dans le problème.

Les conditions aux limites sont les suivantes :

• pas de flux entrant à la surface (origine des coordonnées spatiales x ou τ, axe dirigé vers l'intérieur du milieu)

${\displaystyle L(0,\mu )=0\,,\qquad 0<\mu \leq 1}$

• source plane située à l'infini, entraînant un flux F₀ < 0 donné, le flux d'énergie étant défini par

${\displaystyle F(\tau )=2\pi \int _{-1}^{1}L(\tau ,\mu )\mu {\text{d}}\mu }$

On remarque que pour une distribution isotrope le flux est nul, l'énergie étant également propagée dans toutes les directions.

Le problème consiste à calculer la luminance sortante ou tout au moins la fonction de phase (la distribution angulaire) de celle-ci.

${\displaystyle L(0,\mu )\,,\qquad -1\leq \mu <0}$

On peut donner pour ce problème[4] les propriétés suivantes sur les premiers moments de la luminance :

• le flux d'énergie ou exitance est constant ;
• la pression radiative augmente linéairement avec la profondeur optique.

On peut donner[4] - [5] une solution formelle de l'équation sous la forme

${\displaystyle L(\tau ,\mu )=\left\{{\begin{array}{lr}~~\int _{0}^{\tau }S(t)e^{-{\frac {\tau -t}{\mu }}}{\frac {{\text{d}}t}{\mu }}&~0<\mu \leq 1\\[0.6em]-\int _{\tau }^{\infty }S(t)e^{\frac {t-\tau }{\mu }}{\frac {{\text{d}}t}{\mu }}&-1<\mu \leq 0\end{array}}\right.}$

Par intégration on obtient l'équation intégrale de Milne

${\displaystyle S(\tau )={\frac {1}{2}}\int _{0}^{\infty }S(t)E_{1}(|t-\tau |)\mathrm {d} t}$

où E₁ est l'exponentielle intégrale.

En particulier on voit que la solution du problème est donnée par une transformée de Laplace

${\displaystyle L(0,\mu )=-\int _{0}^{\infty }S(t)e^{\frac {t}{\mu }}{\frac {\mathrm {d} t}{\mu }}\,,\qquad -1<\mu \leq 0}$

Fonction de phase du rayonnement émergent.

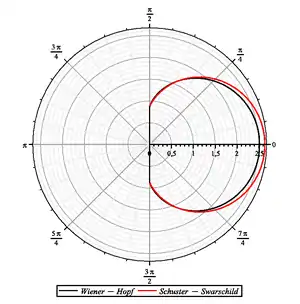
Arthur Schuster (1905)[6] et Karl Schwarzschild (1906)[7] ont donné une solution approchée en séparant les intensités dans les deux sens de propagation opposés, méthode rendue possible par la linéarité de l'équation de Boltzmann. Cette méthode est connue sous le nom d'« approximation à deux flux ».

Soit L⁺ la luminance constituée par une valeur angulaire constante dans le demi-espace x positif et valant 0 dans le demi-espace négatif. L⁻ est son complémentaire, alors, en introduisant ces expressions dans l'équation de Boltzmann il vient

${\displaystyle {\begin{array}{lcl}~~{\frac {1}{2}}{\frac {\mathrm {d} L^{+}}{\mathrm {d} \tau }}&=&-L^{+}+{\frac {1}{2}}(L^{+}+L^{-})\\[0.6em]-{\frac {1}{2}}{\frac {\mathrm {d} L^{-}}{\mathrm {d} \tau }}&=&-L^{-}+{\frac {1}{2}}(L^{+}+L^{-})\end{array}}}$

La condition en τ = 0 est

${\displaystyle L^{+}(0)=0}$

En termes d'énergie et de flux la solution de ce système s'écrit

${\displaystyle F=F_{0}\,,\qquad E(\tau )=-{\frac {2F_{0}}{c}}(1+\tau )}$

En oubliant l'hypothèse qui a conduit à ce résultat on peut recalculer une solution générale du problème en utilisant ce qui a été baptisé plus haut « solution formelle » (cas μ < 0)

${\displaystyle L(\tau ,\mu )=-{\frac {F_{0}}{\pi }}(1+2\tau +2\mu )}$

En particulier la luminance émergente est

${\displaystyle L(0,\mu )=-{\frac {F_{0}}{\pi }}(1+2\mu )}$

Cette solution constitué une bonne approximation de la solution rigoureuse (voir courbe).

Problème de Milne. Calcul S₆₀.

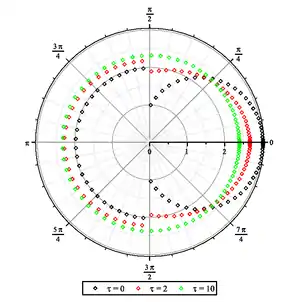
Les solutions font appel

• soit à la méthode SN (ou méthode des ordonnées discrètes) conduisant à une solution semi-analytique[4].

• soit à la méthode de Wiener-Hopf[2] - [8] - [9] - [5] utilisant la transformation de Laplace,
• soit à l'étude des valeurs propres singulières de l'opérateur de transport associé à l'équation de Boltzmann[3].

Les longs calculs mènent à la fonction de phase suivante[2] - [5]

${\displaystyle {\begin{array}{lcl}L(0,\mu )&=&{\frac {\sqrt {3}}{2}}(1-\mu )\exp {\left[{\frac {-\mu }{\pi }}\int _{0}^{\frac {\pi }{2}}{\frac {\log {\left({\frac {\sin ^{2}x}{1-x\cot x}}\right)}}{1-(1-\mu ^{2})\sin ^{2}{x}}}\mathrm {d} x\right]}\,,\qquad -1<\mu \leq 0\\&=&{\frac {1}{2{\sqrt {1-\mu }}}}\exp {\left[{\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}{\frac {x\arctan {(-\mu \tan {x})}}{1-x\cot x}}\mathrm {d} x\right]}\end{array}}}$

En particulier l'émission rasante vaut

${\displaystyle L(0,0)={\frac {\sqrt {3}}{2}}}$

La figure montre le processus par lequel la luminance quasi-isotrope pour τ > 10 se déforme dans la région proche de la paroi.

• Diffusion des ondes
• Structure stellaire
• Méthode SN
• Fonction de Bickley-Naylor