Pouvoir d'arrêt (rayonnement ionisant)
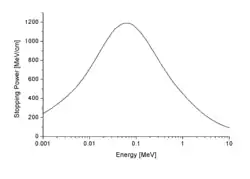
En traversant la matière, les particules chargées ionisent les atomes ou les molécules le long de leur parcours, avec pour conséquence que les particules perdent peu à peu leur énergie. Le pouvoir d'arrêt est la perte moyenne d'énergie de la particule par unité de distance parcourue, mesurée par exemple en MeV/cm (voir la figure ci-contre).
Pouvoir d'arrêt et parcours
Le pouvoir d'arrêt dépend du type de particule, de son énergie et des propriétés de la matière traversée. Parce que la production d'une paire d'ions (typiquement un ion positif et un électron) requiert une quantité moyenne fixe d'énergie (par exemple, à peu près 33 eV dans l'air), la densité d'ionisation est proportionnelle au pouvoir d'arrêt du matériau.
Les électrons, les ions atomiques, les mésons etc. perdent tous de l'énergie en traversant la matière. Ici, nous considérons surtout des ions atomiques.
Le pouvoir d'arrêt mesure une propriété du matériau, tandis que la perte d'énergie par cm considère la situation du point de vue de la particule. Mais la valeur et les unités sont les mêmes et cette valeur est normalement positive, à cause du signe moins devant la définition suivante :
où est l'énergie, et est la distance parcourue. Le pouvoir d'arrêt, et par conséquent la densité d'ionisation, augmentent normalement avec la décélération, ce que montre la courbe de Bragg, nommée d'après William Henry Bragg. Un peu avant la fin du parcours, la perte d'énergie passe par un maximum, le pic de Bragg. Ce pic est primordial en radiothérapie.
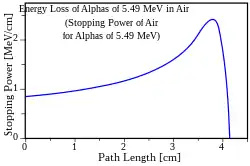
Dans la figure ci-contre, on voit que le pouvoir d'arrêt des particules α de 5,49 MeV dans l'air augmente avant d'atteindre un maximum (cette énergie correspond à la désintégration α du gaz radon 222Rn qui est présent dans l'atmosphère des lieux composé de granite).
L'équation ci-dessus définit le pouvoir d'arrêt linéique qui peut être exprimé en unités comme par exemple MeV/mm. Très souvent, S(E) est divisé par la densité du matériau. De cette manière, on obtient le pouvoir d'arrêt massique qui peut être exprimé en unités comme par exemple MeV/mg/cm2. Le pouvoir d'arrêt massique ne dépend pas de la densité, approximativement.
On peut calculer le parcours moyen en intégrant la réciproque du pouvoir d'arrêt S(E) sur la quantité d'énergie.
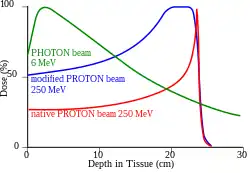
La figure de gauche montre l'absorption par l'eau d'un faisceau de protons accélérés à 250 MeV (courbe rouge); cette courbe a un pic très aigu. Pour irradier une tumeur plus épaisse en radiothérapie, on peut élargir cette pointe en faisant varier l'énergie de l'accélérateur ou en utilisant un matériau absorbant (courbe bleue).
Cette figure montre également l'absorption d'un faisceau de photons de haute énergie (courbe verte). Cette courbe est tout à fait différente. Elle a essentiellement une décroissance exponentielle après un passage par un maximum appelé crête de Tavernier du nom du physicien belge Guy Tavernier qui découvrit le phénomène en 1948. Cette allure de courbe est également celle que l'on obtient pour des faisceaux de neutrons et les rayons X et gamma. Le photon ne perd pas son énergie progressivement par des ionisations successives, mais il perd souvent toute son énergie en une seule ionisation. L'absorption des photons n'est pas décrite par le pouvoir d'arrêt, mais par un coefficient d'absorption.
Pouvoir d'arrêt électronique, nucléaire et radiatif
Le pouvoir d'arrêt électronique provient du ralentissement par les collisions inélastiques entre les électrons du matériau et l'ion passant. Ces collisions engendrent des excitations et des ionisations des électrons du matériau, ainsi que des électrons de l'ion.
Au-dessus d'une énergie d'environ cent keV par nucléon, on peut calculer le pouvoir d'arrêt électronique avec une précision de quelques pour cent, en utilisant par exemple la formule de Bethe. Pour les énergies plus basses, le calcul devient plus difficile[1].
On trouve en ligne les valeurs expérimentales du pouvoir d'arrêt électronique pour beaucoup d'ions et de matériaux[2]. La précision de ces tables de pouvoir d'arrêt électronique a été analysée par exemple par H. Paul[3].
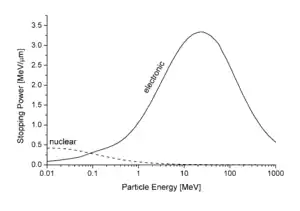
Le pouvoir d'arrêt nucléaire est produit par les collisions élastiques entre l'ion et les atomes du matériau (cependant, l'expression nucléaire n'a rien à voir avec les forces nucléaires, c'est-à-dire l'interaction forte[4]). Si la forme du potentiel répulsif entre l'ion et l'atome est connue, on peut calculer le pouvoir d'arrêt nucléaire . Sur la figure en haut de l'article pour les protons dans l'aluminium, la contribution nucléaire est négligeable partout, sauf pour les plus basses énergies. Mais si la masse de l'ion est plus grande, la contribution nucléaire augmente également. Sur l'image ci-contre, pour des ions aluminium, le pouvoir d'arrêt nucléaire à basse énergie est déjà plus grand que le pouvoir d'arrêt électronique.
Par conséquent, pour les énergies pas trop importantes, le pouvoir d'arrêt est la somme de deux contributions : . Aux énergies plus élevées, on doit considérer également le pouvoir d'arrêt radiatif généré par l'émission du rayonnement continu de freinage dans le champ électrique des noyaux du matériau traversé[4].
Il existe différents modèles semi-empiriques pour calculer le pouvoir d'arrêt, notamment le modèle de Ziegler, Biersack et Littmark décrit à l'origine dans leur ouvrage[5] et désormais largement utilisé par l'intermédiaire de programmes téléchargeables[6].
Références
- (en) P. Sigmund, Particle Penetration and Radiation Effects : General Aspects and Stopping of Swift Point Charges, Springer, coll. « Solid-state sciences », , 437 p. (ISBN 978-3-540-31713-5, présentation en ligne)
- Une collection de mesures expérimentales compilée par H. Paul sur le site de l'université de Linz
- (en) H. Paul, A comparison of recent stopping power tables for light and medium-heavy ions with experimental data, and applications to radiotherapy dosimetry, vol. 247 issue 2, Elsevier Science, coll. « Nucl. Instrum. Methods Phys. Res. B », (ISSN 0168-583X, présentation en ligne), p. 166-172
- ICRU Report 60: Fundamental Quantities and Units for Ionizing Radiation. International Commission on Radiation Units and Measurements, Bethesda, MD, USA (1998)
- J. F. Ziegler, J. P. Biersack et U. Littmark, The Stopping and Range of Ions in Matter, vol. 1, Pergamon Press, (ISBN 0-08-021603-X)
- La page de téléchargement du logiciel SRIM chez J.F. Ziegler