Formule de Bethe

La version relativiste de la formule s'écrit :

${\displaystyle -{\frac {dE}{dx}}={\frac {4\pi }{m_{e}c^{2}}}\cdot {\frac {nz^{2}}{\beta ^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}c^{2}\beta ^{2}}{I\cdot (1-\beta ^{2})}}\right)-\beta ^{2}\right]}$

où

${\displaystyle \beta }$	${\displaystyle =v/c}$
${\displaystyle v}$	vitesse de la particule
${\displaystyle E}$	énergie de la particule
${\displaystyle x}$	longueur du chemin
${\displaystyle c}$	vitesse de la lumière
${\displaystyle z\,e}$	charge de la particule
${\displaystyle e}$	charge élémentaire
${\displaystyle m_{e}}$	masse au repos de l’électron
${\displaystyle n}$	densité numérique des électrons du matériau
${\displaystyle I}$	potentiel d’excitation moyen du matériau

Ici, la densité numérique des électrons du matériau peut être calculée en utilisant ${\displaystyle n={\frac {N_{A}\cdot Z\cdot \rho }{A\cdot M_{u}}}}$, où ${\displaystyle \rho }$ est la densité du matériau, Z et A le nombre atomique et nombre de masse, respectivement, ${\displaystyle M_{u}}$ = 1 g/mol la constante de masse molaire et ${\displaystyle N_{A}}$ le nombre d'Avogadro.

Pouvoir d'arrêt d'aluminium pour protons en fonction de l'énergie des protons, et la formule de Bethe sans (rouge) et avec corrections (bleu)

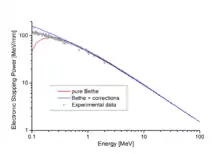
Dans l'image ci-contre, les petits cercles sont des résultats expérimentaux obtenus par des auteurs variés (prises de http://www.exphys.jku.at/Stopping/) ; la courbe est la formule de Bethe. Il est évident que la formule de Bethe est en excellent accord avec les expériences à hautes énergies, notamment si les corrections (voir plus bas) sont ajoutées.

La formule de Bethe est souvent appelée formule de Bethe-Bloch, même lorsqu'elle n'inclut pas l'approximation de Bloch (I=(10ev)×Z).

Pour les petites énergies, la formule de Bethe peut être simplifiée à

${\displaystyle -{\frac {dE}{dx}}={\frac {4\pi nz^{2}}{m_{e}v^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}v^{2}}{I}}\right)\right]}$.

Par conséquent, à basse énergie, le pouvoir d'arrêt selon la formule de Bethe décroît à peu près comme ${\displaystyle 1/v^{2}}$ quand l'énergie croît. Il arrive à un minimum, approximativement à ${\displaystyle E=3Mc^{2}}$, où ${\displaystyle M}$ est la masse de la particule (pour les protons, cela serait à 3000 MeV). Pour les énergies très relativistes, ${\displaystyle (\beta \approx 1)}$, la perte d'énergie croît de nouveau, d'une manière relativiste.

La formule de Bethe est valable seulement pour les énergies assez grandes pour que la particule chargée (l'ion) ne porte pas avec elle des électrons atomiques . À des énergies plus petites, si l'ion porte des électrons, sa charge est réduite effectivement, et par conséquent, le pouvoir d'arrêt est réduit aussi. Mais même si la particule est complètement ionisée, on a besoin de corrections.

Bethe a trouvé sa formule en utilisant un développement perturbatif en mécanique quantique. Par conséquent, son résultat est proportionnel à la charge ${\displaystyle z}$ de la particule au carré. La formule peut être améliorée en considérant des corrections correspondant à des puissances plus élevées de ${\displaystyle z}$. Elles sont : l'effet Barkas-Andersen (proportionnel à ${\displaystyle z^{3}}$, d'après Walter H. Barkas (en) et Hans Henrik Andersen (en)), et la correction Bloch (proportionnel à ${\displaystyle z^{4}}$). En outre, il est nécessaire de considérer que les électrons atomiques de la matière ne sont pas stationnaires (« shell correction »).

Ces corrections ont été introduites, par exemple, dans les programmes PSTAR et ASTAR qu'on utilise pour calculer le pouvoir d'arrêt des protons et des particules alpha[3]. Les corrections sont larges à basse énergie, et elles deviennent de plus en plus petites lorsque l'énergie croît.

Pour les énergies très grandes, il est nécessaire d'ajouter[4] la correction densité de Fermi.

• Pouvoir d'arrêt (rayonnement ionisant)

• Passage des particules chargées par la matière (en anglais)

• Pouvoir d'arrêt pour protons et particules alpha (en anglais)

• Pouvoir d'arrêt: dates et graphiques (en anglais)