Potentiel de Morse
Le potentiel de Morse, nommé d'après le physicien Philip Morse, est un modèle pratique d'énergie potentielle pour une molécule diatomique. C'est une meilleure approximation pour la structure vibrationnelle de la molécule que celle de l'oscillateur harmonique quantique car il comprend de manière explicite les effets d'une rupture de liaison, comme l'existence des états non liés. Il prend aussi en compte l'anharmonicité des liaisons réelles et la probabilité non nulle de transition pour les états harmoniques et les bandes de combinaison.
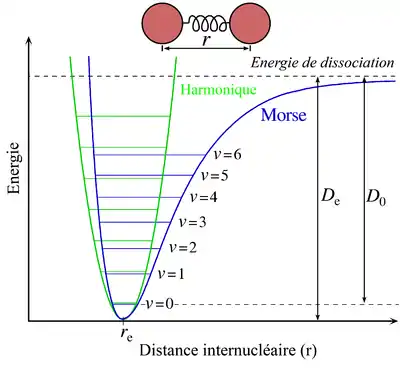
Fonction d'énergie potentielle
La fonction d'énergie potentielle de Morse est de la forme : . où r est la distance entre atomes, re est la longueur de la liaison à l'équilibre, De est la profondeur du puits (définie par rapport aux atomes dissociés) et a contrôle la « largeur » du potentiel. L'énergie de dissociation de la liaison peut être calculée en soustrayant l'énergie de point zéro E(0) de la profondeur du puits. La constante de force de la liaison peut être trouvée en prenant la dérivée de la fonction d'énergie potentielle, à partir de laquelle on peut montrer que le paramètre, a, est : , où ke est la constante de force au minimum du puits.
Le zéro d'énergie potentielle est bien sûr arbitraire, et l'équation du potentiel de Morse peut être réécrite en y ajoutant ou y soustrayant une constante.
Énergie vibrationnelle
Les états stationnaires d'un potentiel de Morse ont les valeurs propres : où v est le nombre quantique de vibration, et ν0 a une dimension de fréquence, et est mathématiquement reliée à la masse de la particule, m, et aux constantes de Morse par : .
Alors que l'espace énergétique entre niveaux vibrationnels de l'oscillateur harmonique quantique est constant à hv0, l'énergie entre niveaux adjacents décroît lorsque v croît pour l'oscillateur de Morse. Mathématiquement, l'espace entre les niveaux de Morse est : . Ce comportement correspond à l'anharmonicité des molécules réelles. Cependant, cette équation échoue pour certaines valeurs de v pour lesquelles E(v + 1) – E(v) est nulle ou négative. Ceci est dû au nombre fini de niveaux de liaisons dans le potentiel de Morse, et aux v, vm qui maintiennent la liaison. Pour les énergies supérieures à vm, tous les niveaux d'énergie possible sont permis et l'équation pour E(v) n'est plus valable.
En dessous de vm, E(v) est une bonne approximation de la structure vibrationnelle réelle dans les molécules diatomiques ne pivotant pas. En fait, les spectres moléculaires réels sont généralement lissés par la formule suivante[1] où les constantes ωe et ωeχe peuvent être directement liés aux paramètres du potentiel de Morse.
Résolution de l'équation de Schrödinger pour l'oscillateur de Morse
Comme pour l'oscillateur harmonique quantique, les énergies et états propres du potentiel de Morse peuvent être trouvés en utilisant des méthodes par opérateurs. Une des approches possible est l'application d'une factorisation au hamiltonien.
Il est aussi possible de résoudre l'équation de Schrödinger directement. Par exemple pour le potentiel , l'équation de Schrödinger indépendante du temps s'écrit:
Pour simplifier cette équation on définit les variables :
.
De plus on a que :
.
Ainsi l'équation de Schrödinger devient :
.
On écrit k0x0 = n + e + 1/2 puis on étudie les comportements asymptotiques de l'équation.
Pour z → +∞, l'équation devient qui a pour solution e-z/2. Pour z → 0, l'équation devient qui a pour solution ze.
Ainsi on choisit l'Ansatz suivant avec ϕ(z) une fonction à déterminer, on trouve : .
qui correspond à l'équation hypergéométrique confluente :
,
qui a pour solution la fonction hypergéométrique confluente
où (a)n désigne le symbole de Pochhammer (c'est-à-dire (x)n = x(x – 1)(x -2)...(x - n +1)).
Ainsi et la solution de l'équation de Schrödinger est
- .
Notes et références
Notes
- CRC Handbook of chemistry and physics, Ed David R. Lide, 87th ed, Section 9, Spectroscopic constants of diatomic molecules p. 9-82.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Morse potential » (voir la liste des auteurs).
- P. M. Morse, Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys. Rev. 1929, 34, 57-64. DOI 10.1103/PhysRev.34.57
- I.G. Kaplan, in Handbook of Molecular Physics and Quantum Chemistry, Wiley, 2003, p207.


![{\displaystyle E(v)=h\nu _{0}(v+1/2)-{\frac {\left[h\nu _{0}(v+1/2)\right]^{2}}{4D_{e}}}}](https://img.franco.wiki/i/4fbddb6948127356e8cdd74c1df8f30f0e72ad0b.svg)
















