Potentiel de Rydberg-Klein-Rees

Figure 1 - Principe de la méthode RKR.

Figure 2 - Quantification. ${\displaystyle D_{e}}$ est la profondeur du puits de potentiel.

Dans l'approximation Brillouin-Kramers-Wentzel l'équation de Schrödinger s'écrit :

${\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dr^{2}}}+V_{J}(r)\right]\psi (r)=E\,\psi (r)\,,\quad V_{J}(r)=V(r)+{\frac {\hbar ^{2}}{2mr^{2}}}J(J+1)}$

où :

• ${\displaystyle m=\left(m_{1}^{-1}+m_{2}^{-1}\right)^{-1}}$ : masse réduite des deux atomes,
• ${\displaystyle V(r)}$ : potentiel électronique,
• ${\displaystyle J}$ : nombre quantique du moment angulaire total,
• ${\displaystyle \psi (r)}$ : fonction d'onde,
• ${\displaystyle E}$ : énergie.

La solution est recherchée sous la forme suivante :

${\displaystyle \psi (r)=e^{\frac {iS(r)}{\hbar }}}$

En reportant dans l'équation de Shrödinger on obtient :

${\displaystyle i\hbar {\frac {d^{2}S}{dr^{2}}}-\left({\frac {dS}{dr}}\right)^{2}+2m(E-V_{J})=0}$

Compte tenu de la valeur de ${\displaystyle \hbar }$ on peut négliger le premier terme de cette équation dont la solution est alors :

${\displaystyle S(r)\simeq \pm \hbar \int _{0}^{r}Q(r')dr'\,,\quad Q(r)={\sqrt {{\frac {2m}{\hbar ^{2}}}(E-V_{J})}}}$

En dérivant cette expression et en reportant dans l'équation de Schrödinger on obtient une solution à l'ordre 1 de la fonction d'onde :

${\displaystyle \psi ^{(1)}(r)={\frac {A}{\sqrt {|Q(r)|}}}e^{\pm i\int _{0}^{r}Q(r')dr'}}$

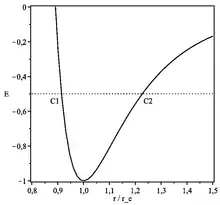
Cette approximation n'est pas bonne dans le voisinage des points tournants (points C₁ et C₂ de la figure 1) où ${\displaystyle Q\simeq 0}$. Toutefois une approximation linéaire locale du potentiel est possible : la solution correspondante est une fonction d'Airy.

La condition de quantification est que l'intégrale de Q entre C₁ et C₂ soit un multiple demi-entier de π[6].

${\displaystyle \left(\nu +{\frac {1}{2}}\right)\pi =\int _{r_{1}}^{r_{2}}Qdr}$

où ${\displaystyle \nu }$ est le nombre quantique vibrationnel.

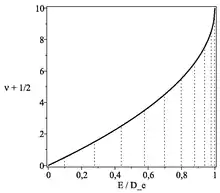
Il s'agit d'une équation sur les valeurs propres illustrée sur la figure 2 :

${\displaystyle {\sqrt {\frac {2m}{\hbar ^{2}}}}\int _{r_{1}(E)}^{r_{2}(E)}\left(E-V_{J}\right)^{\frac {1}{2}}dr=\left(\nu +{\frac {1}{2}}\right)\pi }$

Il existe diverses méthodes permettant de remonter au potentiel à partir de la donnée du spectre[7]. Elles sont basées sur deux types d'approche.

• (en) Robert J. Le Roy, « University of Waterloo, Department of Chemistry, Computer Programs: RKR1-16 »

• Potentiel sphères dures
• Potentiel de Lennard-Jones
• Potentiel de Buckingham
• Potentiel de Stillinger-Weber
• Potentiel de Sutherland
• Potentiel de van der Waals