Onde de Stokes

Ondes de Stokes d'ordre 1 (sinusoïdale) et 2 en milieu peu profond.

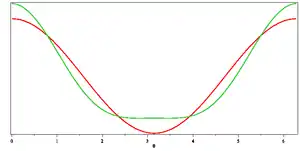
On cherche une solution au système constitué par les équations [1], [2], [3], [4] sous forme d'ondes périodiques progressives

${\displaystyle s=s(\theta )\,,\quad \psi =\psi (z,\theta )\,,\quad \theta =kx-\omega t=k(x-ct)}$

où θ est la phase de l'onde, k le nombre d'onde et c la vitesse de phase.

Pour s, on utilise un développement en série de Fourier autour de la solution de repos (s = 0)

${\displaystyle s=a\cos(\theta )+\mu _{2}a^{2}\cos(2\theta )+...}$

où a est l'amplitude.

Il lui correspond le développement suivant pour ψ[4], suggéré par la solution du problème linéarisé[5]

${\displaystyle \psi =\nu _{0}\,a^{2}t+\nu _{1}\,a\sin {\theta }+\nu _{2}\,a^{2}\sin {2\theta }\cosh(2k(z+h_{0})+...)}$

Pour ω, on choisit une forme paire de l'amplitude compatible avec la périodicité en s (ψ n'est pas nécessairement périodique)

${\displaystyle \omega =\omega _{0}(k)+a^{2}\omega _{2}(k)+...}$

La solution du système limité au second ordre conduit aux résultats suivants[4]

• relation de dispersion

${\displaystyle {\frac {\omega ^{2}}{gk\tau }}=1+\left({\frac {9\tau ^{4}-10\tau ^{2}+9}{8\tau ^{4}}}\right)k^{2}a^{2}+...\,,\qquad \tau =\tanh {kh_{0}}}$

• coefficients du développement pour s

${\displaystyle \mu _{2}=ka{\frac {3-\tau ^{2}}{4\tau ^{3}}}}$

μ₂ est le rapport des amplitudes des deux premières composantes de l'onde.

• coefficients du développement pour ψ

${\displaystyle \nu _{0}={\frac {gk}{2\sinh(kh_{0})}}\,,\qquad \nu _{1}={\frac {\omega _{0}}{k\sinh(kh_{0})}}\,,\qquad \nu _{2}={\frac {3\omega _{0}}{\sinh ^{4}(kh_{0})}}}$

• Vitesse de phase

${\displaystyle c={\frac {g\tau }{k}}}$

On a en particulier

• en eau profonde (k h₀ → ∞

${\displaystyle kh_{0}\rightarrow \infty \,,\quad \omega ^{2}\simeq gk[1+(ka)^{2}]\,,\qquad \qquad \quad \mu _{2}\simeq {\frac {1}{2}}ka}$

L'approche est valide pour des hauteurs de vague de faible amplitude devant la longueur d'onde

${\displaystyle \mu _{2}<<1\quad \Rightarrow \quad a<<\lambda }$

où λ = 2π/k la longueur d'onde.

• en eau peu profonde k h₀ → 0

${\displaystyle kh_{0}\rightarrow 0\,,\;\;\quad \omega ^{2}\simeq gh_{0}k^{2}\left[1+{\frac {9(ka)^{2}}{8(kh)^{4}}}\right]\,,\qquad \mu _{2}\simeq {\frac {3}{32\pi ^{2}}}\,{\mathcal {U}}\,,\quad {\mathcal {U}}={\frac {H\lambda ^{2}}{h_{0}^{3}}}}$

où U le nombre d'Ursell.

Pour une eau peu profonde l'approche est utilisable lorsque

${\displaystyle \mu _{2}<<1\quad \Rightarrow \quad {\mathcal {U}}<<{\frac {32\pi ^{2}}{3}}\simeq 100}$

• Il existe des solutions pour un développement jusqu'à l'ordre 5[6].
• L'approche peut être utilisée pour des ondes stationnaires[7] ou aléatoires[8] - [9].
• Tullio Levi-Civita a démontré la convergence des développements utilisés pour des ondes de faible amplitude et un milieu de profondeur infinie[10]. Ce résultat a été étendu aux milieux à profondeur finie par Dirk Jan Struik[11].
• Thomas Brooke Benjamin et Jim E. Feir on montré l'instabilité de la solution pour les fortes profondeurs[12]. L'instabilité de Benjamin-Feir peut conduire à la formation d'une vague scélérate[13].

• (en) Graham W. Griffiths et William E. Schiesser, « Linear and Nonlinear Waves », sur Scholarpedia
• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Stokes wave » (voir la liste des auteurs).

• Onde cnoïdale
• Équations de Boussinesq
• Équations de Barré de Saint-Venant
• Équation de Korteweg-de Vries
• Équation de Whitham
• Tsunami