Oméga de Chaitin

Émile Borel s'est intéressé à la notion « d'accessibilité » et de définition d'un nombre. Selon Borel, pour qu'un nombre soit « bien spécifié », il faut d'une part que « deux mathématiciens, s’ils en parlent entre eux, soient certains qu’ils parlent du même nombre » et qu'il soit un « véritable “être” mathématique » qui doit « pour être intéressant aux yeux des mathématiciens, avoir au moins deux propriétés (en y comprenant celle au moyen de laquelle il a été défini) »[3]. Il est effectivement très difficile pour un nombre purement aléatoire de posséder une autre propriété que sa propre méthode de construction.

D'autre part, Borel a imaginé en 1927 un nombre réel, le « nombre qui sait tout » (terminologie de G. Chaitin[Chaitin 2007 1]), résumant les réponses à toutes les questions formulables dans un langage donné, auxquelles on peut répondre par oui ou par non[4]. Cette liste de questions constitue une liste infinie, mais dénombrable, que l'on peut trier alphabétiquement. On peut alors constituer un nombre, unique et bien spécifié, dont la n-ième décimale binaire est la réponse à la n-ième question.

Ces deux idées contiennent les germes du nombre Oméga. Chaitin, qui connaît très bien l'œuvre de Borel, reconnaît s'être inspiré de ces idées. Mais tout le travail de Chaitin va consister à transformer une idée mathématiquement inexploitable (car les questions et les réponses ne peuvent être mathématiquement formalisées), en un véritable « être mathématique », possédant de nombreuses propriétés démontrables, et deux caractéristiques a priori contradictoires : être « bien spécifié » et pourtant « inaccessible », non calculable et aléatoire.

Si l'on recycle l'idée du « nombre qui sait tout » pour définir un nombre dont la n-ième décimale répond au problème de l'arrêt pour le n-ième programme exécutable par une machine de Turing universelle, nous avons alors une définition précise d'un nombre et qui possède un sens mathématique, car le problème de l'arrêt est formalisé. De plus, étant donné que le problème de l'arrêt est indécidable (au sens algorithmique), il s'ensuit que ce nombre est non calculable, ce qui est une condition absolument nécessaire (mais non suffisante) pour qu'il soit aléatoire. Enfin, injecter le problème de l'arrêt dans un nombre est susceptible de lui donner une importance fondamentale, car le problème de l'arrêt est au cœur de problèmes fondamentaux des mathématiques (ceux par exemple liés au dixième problème de Hilbert).

Tel quel, ce nombre n'est pas encore le nombre Oméga, car il n'est pas aléatoire. En effet, ce nombre (que Chaitin nomme « nombre de Turing » en hommage à l'inventeur du problème de l'arrêt[Chaitin 2007 2]), est hautement redondant et compressible. Or, une des définitions d'un nombre aléatoire est précisément d'être incompressible[5]. Il faut donc trouver un moyen de compresser l'information contenue dans le nombre de Turing, et de la compresser au maximum possible.

Représentation d'un ensemble de programmes auto-délimités sous forme d'un arbre binaire.
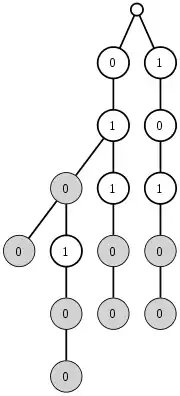
Ici, nous avons quatre programmes possibles, correspondant aux quatre feuilles de l'arbre : "01(00)", "011(00)", "0101(00)", et "101(00)"
La procédure de génération aléatoire d'un programme consiste à tirer au sort chaque bifurcation dans cet arbre.

Pour comprendre comment sera compressé le nombre Oméga, il est utile de voir pourquoi le nombre de Turing est hautement redondant. En fait, le nombre de Turing utilise N bits pour coder les résultats de N programmes, alors que log₂(N) bits sont suffisants. En effet, il suffit de connaître le nombre de programmes de N bits qui s'arrêtent, sans savoir lesquels, pour déterminer les programmes qui s'arrêtent ou non.

Voici comment : si l'on connaît le nombre P de programmes de N bits qui s'arrêtent, alors il suffit de générer tous les programmes de N bits, de faire tourner ces 2^N programmes et de s'arrêter quand P programmes seront arrêtés (ce qui arrivera certainement dans un temps fini). On est alors sûr que les programmes restants ne s'arrêteront jamais. On connaît donc les programmes qui s'arrêtent et ceux qui ne s'arrêtent pas. P est donc un nombre d'au plus N bits codant les résultats du problème de l'arrêt pour 2^N programmes.

Le nombre Oméga va utiliser cette idée pour encoder ces informations de manière efficace et incompressible. Le nombre de programmes d'une machine de Turing universelle donnée étant infini, il n'est pas possible de donner un nombre P de programmes qui s'arrêtent (P serait dans la plupart des cas infini), mais on peut donner cette information par la proportion des programmes qui s'arrêtent parmi tous les programmes, ou — ce qui revient au même — la probabilité d'arrêt d'un programme pris au hasard.

Le nombre Oméga est donc défini comme étant la probabilité qu'un programme, tiré aléatoirement, d'une machine de Turing universelle, s'arrête.

Le tirage aléatoire consiste à descendre aléatoirement dans l'arbre binaire représentant tous les programmes possibles pour une machine de Turing universelle U, jusqu'à tirer aléatoirement une séquence de fin, délimitant objectivement la fin de la représentation binaire du programme (voir figure ci-contre). En effet, la définition, et la formule, du nombre Oméga n'est valide que pour les programmes auto-délimités, c'est-à-dire contenant à leur fin une séquence de bits impossible à trouver dans le programme proprement dit. Le nombre de programmes de cette machine de Turing jusqu'à une profondeur N de l'arbre binaire (autrement dit, le nombre de programmes de longueur inférieure ou égale à N) est le nombre de feuilles de l'arbre.

Pour calculer la probabilité d'arrêt (ou la proportion des programmes qui s'arrêtent), il suffit à première vue de « compter » le nombre de programmes « feuille » qui s'arrêtent, et de diviser par le nombre total de feuilles, mais cela n'est vrai qu'à un niveau N donné. S'il existe un programme court dans l'arbre, on a beaucoup plus de chances de tomber aléatoirement sur lui qu'un programme long : il faut donc « pondérer » l'arrêt d'un programme p de taille |p| par 2^–|p|. Plus un programme est long, plus son poids est faible.

La formule du nombre Oméga en dérive directement ; on additionne les poids pondérés de tous les programmes qui s'arrêtent (P_U est l'ensemble de définition de la machine U, c'est-à-dire l'ensemble de tous les programmes qui retournent un résultat et par conséquent s'arrêtent ; |p| est la longueur en bits du programme p) :

${\displaystyle \Omega _{U}=\sum _{p\in P_{U}}2^{-|p|}}$

Cette somme converge et reste inférieure à 1, car les programmes sont auto-délimités : aucun programme n'est le prolongement d'un autre programme (en intégrant la séquence de fin). Par conséquent, un programme court va empêcher l'arbre de se développer après lui : on peut donc lui donner sans danger de divergence le poids de la partie de l'arbre qu'il a empêché de se développer, soit 2^-|p|. En donnant le bon poids à chaque nœud terminal, on démontre que la somme est majorée par 1, si l'on prend en compte tous les nœuds. Cette propriété est démontrée par les inégalités de Kraft.

Mais le véritable but du nombre Oméga n'est pas de donner la probabilité d'arrêt d'un programme d'une machine de Turing donnée. Son but est de compresser sous la forme la plus compacte possible l'information d'arrêt de tous les programmes de cette machine de Turing. Il est donc nécessaire d'être en mesure de restituer ces informations à partir de la probabilité d'arrêt.

Soit Ω_n l'approximation d'un nombre Oméga consistant à prendre les n premiers bits de ce nombre Oméga. Comment, étant donné ce nombre Ω_n, déterminer les programmes de longueur inférieure à n bits qui s'arrêtent ou non ?

L'inégalité ${\displaystyle \Omega _{n}\leq \Omega <\Omega _{n}+2^{-n}}$ découle logiquement de la convergence de la somme associée à Ω.

Si maintenant on génère tous les programmes possibles de taille inférieure ou égale à n bits, et si on les fait exécuter simultanément, on pourra calculer une approximation de plus en plus précise de Ω_n à chaque arrêt d'une machine, en ajoutant ${\displaystyle 2^{-l}}$, l étant la longueur du programme s'étant arrêté, à l'approximation précédente.

Dès que l'approximation de Ω_n atteint une valeur telle que l'ajout du poids d'un programme quelconque non encore terminé rendrait l'approximation supérieure ou égale à ${\displaystyle \Omega _{n}+2^{-n}}$, nous pouvons être certain que les programmes restants ne se termineront jamais. Les programmes de longueur inférieure ou égale à n qui ne s'arrêtent pas ont donc été identifiés dans un temps fini, à l'aide des n premier bits du nombre Oméga : Ω_n[Li Vitanyi 1].

On établit au passage la propriété : les n premiers bits d'un nombre Oméga sont nécessaires et suffisants pour déterminer l'arrêt de tous les programmes de longueur inférieure à n bits.

Soit un nombre ω_n représentant le nombre le plus court possible permettant de déterminer le problème de l'arrêt pour tous les programmes jusqu'à une longueur de n bits.

Soit le programme COMPLEXE qui, en utilisant ce nombre, détermine la liste des machines qui s’arrêtent de longueur inférieure ou égale à n bits, collectionne tous les résultats de ces machines, et retourne un nombre x n'appartenant pas à cette liste. Le programme COMPLEXE s'arrête.

Par définition, x ne peut être retourné par un programme de taille inférieure ou égale à n. COMPLEXE retournant ce nombre, il possède donc une taille supérieure à n. Comme COMPLEXE intègre ω_n dans son programme, il s'ensuit que TAILLE(COMPLEXE) = TAILLE(ω_n) + constante > n[Li Vitanyi 2].

Le plus petit programme pour calculer les n premiers bits de Ω a une taille supérieure à n – constante, ce qui est la caractéristique d'un nombre aléatoire au sens de Levin-Chaitin. Oméga est donc bien incompressible et aléatoire.

La connaissance d'un Oméga de Chaitin permettrait, en théorie, de résoudre certains problèmes en théorie des nombres, dont certains non résolus à ce jour comme la conjecture de Goldbach et l'hypothèse de Riemann[6].

Par exemple, la conjecture de Goldbach affirme que tout nombre pair plus grand que 2 est la somme de deux nombres premiers. Pour prouver cette conjecture à l'aide d'un nombre Oméga, il s'agirait de réaliser un programme qui recherche la décomposition de tous les nombres pairs en somme de deux nombres premiers. Pour un nombre pair donné, il est possible pour un programme de déterminer si la conjecture est vraie ou fausse en un temps fini (soit en trouvant la somme, soit en épuisant toutes les possibilités sans en trouver, ce qui serait un contre-exemple à la conjecture). Si le programme trouve un contre-exemple, il s'arrête, sinon il continue de chercher un contre-exemple à l'infini.

Donc : si la conjecture de Goldbach est vraie, le programme ne s'arrête pas, si elle est fausse, le programme s'arrête (en retournant un contre-exemple).

En sachant si ce programme se termine ou non en utilisant le nombre Oméga, on pourrait donc savoir avec certitude que la conjecture est vraie ou fausse.

De manière générale, les problèmes mathématiques dont la solution est potentiellement contenue dans un Oméga de Chaitin sont les problèmes réfutables en un temps fini, c'est-à-dire pour lesquels un programme est en mesure de s'arrêter avec un contre-exemple en un temps fini. Tous les problèmes mathématiques ne sont pas réfutables en un temps fini, notamment :

• Est-ce que π est un nombre normal ?
• Existe-t-il une infinité de nombres premiers jumeaux ?
• Le problème P = NP.

ne sont pas réfutables en un temps fini, et leur solution n'est pas contenue dans un nombre Oméga[Li Vitanyi 3]. On peut cependant remarquer que pour une axiomatique donnée (le plus souvent ZFC), ces questions peuvent être considérées comme des affirmations susceptibles d'être démontrées, réfutées, ou indécidables ; un nombre Oméga permet donc, pour une proposition P donnée, de savoir ce qu'il en est des deux machines de Turing énumérant tous les théorèmes et s'arrêtant respectivement si P en est un ou si sa négation en est un.

Cependant, tout cela reste théorique. La méthode pour restituer les machines qui s'arrêtent à partir d'un nombre Oméga (autrement dit, pour « décompresser » un nombre Oméga, voir Détermination des programmes qui s'arrêtent à partir du nombre Oméga) est si longue qu'elle est inapplicable en pratique[7]. En effet, il est nécessaire d'attendre que tous les programmes qui doivent s'arrêter s'arrêtent avant de connaitre le statut de chaque programme[7]. Comme il existe jusqu'à 2^N programmes de longueur N bits, et qu'un programme individuel peut théoriquement s'arrêter au terme d'un temps arbitrairement long, et que l'ordre de grandeur de N pour les problèmes mathématiques intéressants est de l'ordre du millier[8], il serait nécessaire d'attendre l'arrêt de ${\displaystyle 2^{1000}\simeq 10^{301}}$ programmes approximativement, parmi lesquels — plausiblement pour cette classe de programmes — le castor affairé, dont le temps d'arrêt est lui-même incommensurablement long[9].

Un nombre Oméga n'est pas calculable, car il est aléatoire : aucun algorithme qui ne contient pas déjà le nombre en lui-même ne peut donner de manière certaine et dans un temps fini les N premiers bits d'un nombre Oméga. Cependant, le statut de ces nombres vis-à-vis de la calculabilité n'est pas trivial et mérite quelques précisions.

Un nombre Oméga n'est pas un nombre calculable, mais est un nombre approchable[10]. Cela signifie qu'il existe une séquence calculable et jamais décroissante de rationnels qui converge vers ce nombre[Calude 1]. C'est précisément cette caractéristique qui est mise en œuvre dans la « décompression » d'un nombre Oméga, pour calculer une approximation de plus en plus précise d'un nombre Oméga (puisqu'on stoppe la décompression quand l'approximation égale le nombre Oméga).

Le problème est que, même si cette séquence est convergente, on n'a aucun moyen de savoir (cela est non calculable) quels bits du nombre Oméga ou même combien de bits seront exacts au terme de combien de temps. De plus, il a été démontré que la convergence vers un nombre Oméga par une séquence approchante est plus lente que n'importe quelle autre séquence convergente calculable[11]. Même si une séquence approchante calculable existe, elle ne peut donc être utilisée pour calculer en pratique, et même en théorie, un nombre Oméga, qui reste de ce fait bel et bien non-calculable.

Il peut paraître dès lors paradoxal de constater que la valeur exacte des N premier bits de nombres Oméga ont été déterminés pour certaines machines de Turing universelles[Calude 2]. Mais cela ne contredit pas les résultats précédents pour la raison suivante : la détermination de ces bits utilise un mélange de calcul et de raisonnements mathématiques, pour prouver que certains programmes ne s'arrêtent pas ou ne peuvent contribuer significativement à la somme finale. Le raisonnement mathématique étant une sorte de calcul, cette constatation ne semble pas faire avancer le paradoxe.

Seulement, il a été prouvé qu'un système formel mathématique (utilisé pour les raisonnements mathématiques, comme ZFC par exemple) fondé sur des axiomes qui représentent N bits d'information, ne pourra jamais déterminer plus de N+O(1) bits d'un nombre Oméga par des raisonnements mathématiques[Chaitin AIT 1] (le nombre exact de bits que peut déterminer la théorie est incalculable). On peut donc déterminer un certain nombre de bits d'un nombre Oméga, mais un nombre fini, incalculable, et d'autant plus faible que le système formel utilisé pour les raisonnements est élégant, et fondé sur un nombre le plus petit possible d'axiomes[Calude 3].

Un nombre Oméga pose un défi à toute théorie, à tout système formel, mathématique. Chaque bit d'un nombre Oméga représente, indépendamment des problèmes plus profonds qu'il peut résoudre, un théorème mathématique simple :

Chacun de ces théorèmes est soit vrai soit faux dans l'absolu. Le N-ième bit possède une valeur déterminée et univoque, même si elle ne peut pas être calculée : les machines de Turing qui contribuent à la détermination de ce bit s'arrêtent ou bien ne s'arrêtent pas dans l'absolu.

De plus, un nombre Oméga étant incompressible, l'infinité des théorèmes « Oméga N » sont autant de problèmes indépendants à résoudre pour une théorie mathématique. La complexité de tous les théorèmes mathématiques est infinie.

En 1931, Kurt Gödel a démontré l'incomplétude des théories mathématiques par le célèbre théorème d'incomplétude de Gödel : il existe dans toute théorie mathématique suffisamment puissante, des énoncés qui ne sont pas démontrables et dont la négation n'est pas non plus démontrable. Ce sont des énoncés indécidables.

Les nombres Oméga apportent un éclairage complémentaire au théorème d'incomplétude de Gödel. Si l'on ne fait pas appel à la théorie algorithmique de l'information, la portée du théorème de Gödel n'est pas claire : Combien de théorèmes sont indécidables ? Est-ce l'exception ou la règle ? Les théorèmes indécidables se limitent-ils aux théorèmes « diagonaux » incontournables, ou sont-ils beaucoup plus répandus ? Est-il nécessaire d'augmenter le nombre d'axiomes pour diminuer le nombre de problèmes indécidables ? Quelle est la relation entre le nombre d'axiomes et le nombre de théorèmes indécidables ?

La théorie algorithmique de l'information et les nombres Oméga apportent des éléments de réponse à ces questions. En effet, selon la théorie algorithmique de l'information :

1. Le nombre de problèmes (de théorèmes) indépendants (qui ne dérivent pas les uns des autres) à résoudre par les théories mathématiques est infini (il y a, au moins, les théorèmes « Oméga N »). Pratiquement tous les théorèmes « Oméga N » sont indécidables pour un système formel type ZFC[Calude 4] ;
2. La complexité des théorèmes résolus par une théorie mathématique est limitée par la complexité de l'ensemble de ses axiomes. Il s'agit du théorème d'incomplétude de Chaitin (en) ;
3. Donc le seul moyen de diminuer le nombre de problèmes indécidables est d'augmenter le nombre d'axiomes. Le nombre d'axiomes nécessaires pour résoudre les théorèmes « Oméga N » tend vers l'infini.

Selon ce point de vue, le théorème de Gödel a un impact très important sur la complétude des mathématiques : de très nombreux théorèmes, quasiment tous, sont indécidables. Les théorèmes vrais et démontrables sont un ensemble rare parmi l'ensemble des théorèmes vrais[12].

Mais on ne sait pas si des théorèmes « intéressants » des mathématiques ont une grande complexité (dans ce cas, ils seraient hors d'atteinte d'un système formel ayant trop peu d'axiomes), ou une complexité en définitive faible, ce qui est tout à fait possible[13]. De plus, on pourrait arguer du fait que les théorèmes « Oméga N » sont des théorèmes artificiels, concernant un nombre spécialement construit pour être paradoxal, et ne sont pas représentatifs des véritables mathématiques.

Mais on peut démontrer qu'il existe une équation diophantienne ${\displaystyle A(n,x_{1},x_{2},...,x_{m})=0}$, associé à un nombre Oméga, telle qu'elle admet pour solutions un ensemble fini de m-uplets ${\displaystyle (x_{1},x_{2},...,x_{m})}$ si le théorème « Oméga n » est vrai, et un ensemble infini de m-uplets ${\displaystyle (x_{1},x_{2},...,x_{m})}$ si le théorème « Oméga n » est faux pour ce nombre Oméga[Li Vitanyi 4].

En posant les choses de cette manière, les théorèmes « Oméga N » ne sont plus des théorèmes artificiels concernant un nombre étrange, mais d'authentiques problèmes mathématiques s'intéressant au nombre de solutions d'une équation.

Les nombres Ω présentent maintes propriétés intéressantes et surprenantes.

• Un nombre Ω n'est pas calculable au sens de Turing : s'il l'était, on pourrait déterminer le problème de l'arrêt.
• Un nombre Ω est transcendant, puisqu'il n'est pas calculable, et son développement binaire, décimal ou dans n'importe quelle base, est donc infini non périodique.
• Le produit de deux nombres Ω est un autre nombre Ω (associé à une autre machine universelle), de même que la somme de deux nombres Ω si elle est strictement comprise entre 0 et 1, et toute suite calculable extraite des décimales d'un nombre Ω (comme une décimale sur deux, ou celles de rang premier) est un autre nombre Ω.
• Un nombre Ω est un nombre normal (donc un nombre univers en toute base) : dans toute base de numération, ses décimales sont équiréparties, et toute suite finie de chiffres se trouve quelque part dans son expression dans cette base (dans tout nombre Ω écrit en binaire, il y a par exemple une suite d'un milliard de 0 successifs)[14].
• Pour une théorie axiomatique récursivement axiomatisable qui permet d'interpréter l'arithmétique, par exemple l'arithmétique de Peano ou la théorie des ensembles, et sous une hypothèse de cohérence plus forte que la cohérence simple[15], il existe un rang à partir duquel, bien qu'un des énoncés « le bit suivant du développement binaire est 0 » ou « le bit suivant du développement binaire est 1 » (en binaire) soit vrai, il est impossible de démontrer lequel des deux l'est, c'est-à-dire qu'ils sont indécidables dans la théorie en question. Solovay a renforcé ce résultat, en modifiant astucieusement une fonction universelle de Chaitin, en fonction d'une théorie donnée (vérifiant les mêmes hypothèses), pour exhiber un nombre Ω, qui dépend donc de cette théorie, et dont il est impossible de décider un seul chiffre dans celle-ci[16].

La définition d'une probabilité d'arrêt suppose qu'aucun programme ne résulte de l'extension d'un autre.

On considère une fonction F à deux arguments. F est dite universelle si pour toute fonction calculable f d'une seule variable x il y a une constante p telle que pour tout x, F(p,x) = f(x) ; en d'autres mots, F peut être utilisée pour simuler n'importe quelle fonction calculable d'une seule variable. p représente un programme pour f, et F représente un émulateur qui exécute ce programme ; pour chaque p, f(x) = F(p,x) est calculable.

Le domaine de F est l'ensemble de tous les programmes p tels que F(p,x) soit définie pour au moins une valeur de x. Selon la convention ci-dessus, il n'existe pas dans le domaine deux programmes différents p₁ et p₂ tels que l'un d'eux soit une extension de l'autre : on dit que F est sans préfixe.

Ceci revient à parler de la machine universelle (machine de Turing) correspondant à F dont les programmes ont une séquence de fin.

On considère l'espace de Cantor formé de toutes les suites infinies de 0 et de 1. Une probabilité d'arrêt peut être interprétée comme la mesure d'un certain sous-ensemble de cet espace.

La mesure probabiliste dans cet espace est définie de façon que pour toute chaîne x l'ensemble des suites qui commencent par x mesure 2^-|x|. Ceci entraîne que pour tout entier naturel n l'ensemble des suites f de l'espace de Cantor telles que f(n) = 1 mesure 0,5 et que l'ensemble des suites dont le n-ième élément est 0 mesure aussi 0,5.

Soit F une fonction universelle calculable sans préfixe telle que décrite plus haut. Le domaine P de F est un ensemble infini de chaînes :

${\displaystyle P=\{p_{1},p_{2},\ldots \}.}$

Chaque ${\displaystyle p_{i}}$ détermine un sous-ensemble ${\displaystyle S_{i}}$ de l'espace de Cantor, ce sous-ensemble contient toutes les suites qui commencent par ${\displaystyle p_{i}}$. Les ${\displaystyle S_{i}}$ étant disjoints — puisque par hypothèse aucun des ${\displaystyle p_{i}}$ n'est inclus dans un autre — la somme :

${\displaystyle \sum _{p\in P}2^{-|p|}}$

représente la mesure de P.

De cette façon, Ω_F est la probabilité qu'une suite de l'espace de Cantor choisie au hasard commence par une chaîne qui soit un élément du domaine de ${\displaystyle \quad F}$. C'est pour cette raison que Ω_F s'appelle la probabilité d'arrêt.

• Suite de Specker

(en) Eric W. Weisstein, « Chaitin's Constant », sur MathWorld