Inégalité de Kraft
En théorie des codes, l'inégalité de Kraft donne, étant donné un ensemble de longueurs de mots de code, une condition nécessaire et suffisante pour l'existence d'un code préfixe et d'un code uniquement décodable. L'inégalité de Kraft est nommée d'après Leon Kraft. Elle est publiée par Kraft en 1949[1]. Toutefois, l'article de Kraft traite uniquement des codes de préfixe, et attribue l'analyse menant à l'inégalité à Raymond Redheffer.
Définition formelle
Soit un alphabet et un code uniquement décodable de sur un alphabet de taille , en notant les longueurs des mots de code , alors
Réciproquement, soient satisfaisant l’inégalité de Kraft, alors, il existe un code préfixe de taille sur un alphabet de taille avec ces longueurs de code.
Cas des codes préfixes
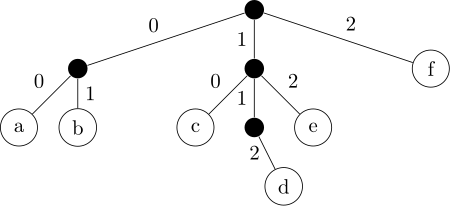
En se restreignant aux codes préfixes, on trouve une démonstration simple du sens direct basée sur la bijection entre les arbres -aires et les codes préfixes
L’inégalité de Kraft devient alors :
Pour tout arbre -aire, avec l’ensemble de ses feuilles, et la profondeur de la feuille :
Réciproquement, il suffit de montrer qu’à partir de satisfaisant l’inégalité de Kraft, on peut construire un arbre -aire avec feuilles vérifiant .
Cas général
Le cas général a un corollaire intéressant : puisque tout code uniquement décodable obéit à l'inégalité de Kraft, et qu'à partir de cette inégalité, on peut construire un code préfixe, pour tout code uniquement décodable, il existe un code préfixe dont les mots codés sont de même taille. Autrement dit, les codes uniquement décodables ne sont pas plus compacts que les codes préfixe.
Remarquons que la réciproque a déjà été traitée dans le cas des codes préfixes, tout code préfixe étant un code uniquement décodable.
Notes et références
- (en) Leon Gordon Kraft, « A device for quantizing, grouping, and coding amplitude-modulated pulses », Massachusetts Institute of Technology (Thèse), (lire en ligne, consulté le )










































