Nombre carré centré
Un nombre carré centré est un nombre figuré centré qui peut être représenté par un carré avec un point placé en son centre et tous ses autres points disposés en couches carrées concentriques de 4 points, 8 points, 12 points, etc. Ainsi, le n-ième carré centré comporte n points sur chaque rayon et sur chaque côté :

C4,1 = 1

C4,2 = 1 + 4 = 5

C4,3 = 5 + 8 = 13
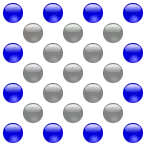
C4,4 = 13 + 12 = 25
Relation de récurrence et formule explicite
Pour tout entier n ≥ 1, le n-ième carré centré a un point central et n – 1 couches carrées.
Pour tout entier n ≥ 2, la dernière couche du n-ième carré centré comporte 4(n – 1) points ; c'est le gnomon associé au (n – 1)-ième carré centré, et faisant passer au n-ième :
Pour tout entier n ≥ 1, le n-ième nombre carré centré égale donc 1 plus 4 fois la somme des entiers de 0 à n – 1 :
Exemple
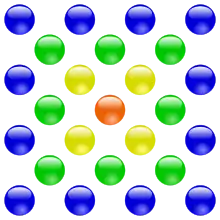
Le quatrième nombre carré centré est :
Liste de nombres carrés centrés
Les dix premiers nombres carrés centrés sont :
Relations avec les nombres triangulaires
- D'après son expression ci-dessus, le n-ième nombre carré centré égale 1 plus 4 fois le (n – 1)-ième nombre triangulaire Tn–1 = n(n – 1)2 :
Cette égalité peut se représenter par :

- Pour tout entier n ≥ 2, le n-ième nombre carré centré est la somme pondérée des trois nombres triangulaires consécutifs Tn–2, Tn–1, Tn, affectés des coefficients 1, 2, 1 :
- Le cas C4,2 = T0 + 2T1 + T2 = 0 + 2×1 + 3 = 5 est trivial ; représentations suivantes :

- 1 est le seul nombre à la fois carré centré et triangulaire. En effet, pour tout entier n ≥ 2, .
Relations avec les nombres carrés
- Pour tout entier n ≥ 1, le n-ième nombre carré centré est la somme des deux nombres carrés consécutifs n2 et (n – 1)2 :

- Pour tout entier n ≥ 1, le n-ième nombre carré centré peut donc aussi s'écrire sous la forme :
(trinôme du second degré sous forme canonique).
- C4, n = m2 si et seulement si (2n – 1)2 – 2m2 = –1.
Les cinq plus petits nombres à la fois carrés centrés et carrés parfaits sont donc : C4, 1 = 1 = 12, C4, 4 = 25 = 52, C4, 21 = 292, C4, 120 = 1692 et C4, 697 = 9852 ( A008844).
A008844).
Propriétés de congruence
- Tous les nombres carrés centrés sont impairs ; et en base 10, le chiffre des unités du n-ième nombre carré centré suit le motif « 1-5-3-5-1 ».
- Tous les nombres carrés centrés et leurs diviseurs sont congrus à 1 modulo 4. (En effet : pour tout facteur premier p de 2n2 – 2n + 1, p est impair, et modulo p, puisque (n – 1)2 est congru à –n2, –1 est un résidu quadratique ; donc modulo 4, p est congru à 1.) Ils se terminent donc par le chiffre 1 ou 5 en bases 6, 8, et 12.
Nombre carré centré premier
Les dix plus petits entiers qui sont à la fois premiers et carrés centrés sont 5, 13, 41, 61, 113, 181, 313, 421, 613, 761 (![]() A027862).
A027862).










