Loi de Dirichlet
En probabilité et statistiques, la loi de Dirichlet, souvent notée Dir(α), est une famille de lois de probabilité continues pour des variables aléatoires multinomiales. Cette loi (ou encore distribution) est paramétrée par le vecteur α de nombres réels positifs et tire son nom de Johann Peter Gustav Lejeune Dirichlet. Elle est vue comme la généralisation multinomiale de la loi bêta.
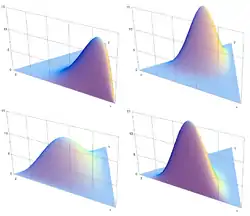
Densité de probabilité
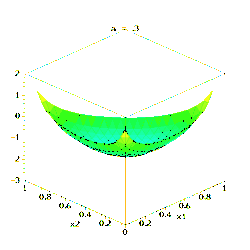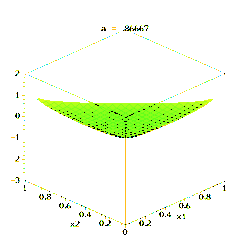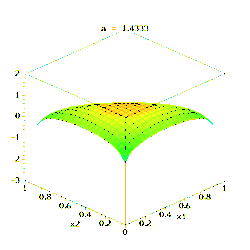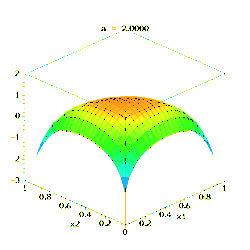
La loi de Dirichlet d'ordre K ≥ 2 de paramètres α1, ..., αK > 0 possède pour densité de probabilité :
pour tous les x1, ..., xK > 0 vérifiant x1 + ... + xK-1 < 1, où xK est une abréviation pour 1 – x1 – ... – xK–1. La densité est nulle en dehors de ce simplexe ouvert de dimension (K − 1).
La constante de normalisation est la fonction bêta multinomiale, qui s'exprime à l'aide de la fonction gamma :
Propriétés
Soit , signifiant que les K – 1 premières composantes possèdent la distribution précédente et que
Posons . Alors
et
En fait, les densités marginales sont des lois bêta :
Qui plus est,
Le mode de la distribution est le vecteur (x1, ..., xK) avec
Agrégation
Si ,alors . Cette propriété d'agrégation permet d'obtenir la distribution marginale de mentionnée plus haut.
Distributions associées
- Si, pour
- , où γ désigne la distribution Gamma, indépendamment
- alors
- et
- Bien que les Xi ne soient pas indépendants, ils peuvent néanmoins générer un échantillon de variables aléatoires, distribuées selon une distribution Gamma. Malheureusement, puisque la somme est perdue lors de la génération de X = (X1, ..., XK), il n'est pas possible de retrouver les variables Gamma initiales.
- Les marginales d'une loi de Dirichlet sont des lois bêta :
Génération de (pseudo-)nombres aléatoires (RNG)
Une méthode pour obtenir un vecteur aléatoire à partir de la distribution de Dirichlet de dimension K de paramètres est fournie par la remarque précédente. Tout d'abord, on tire K variables indépendantes selon des distributions Gamma, chacune avec la densité
et on pose finalement
Interprétations intuitives des paramètres
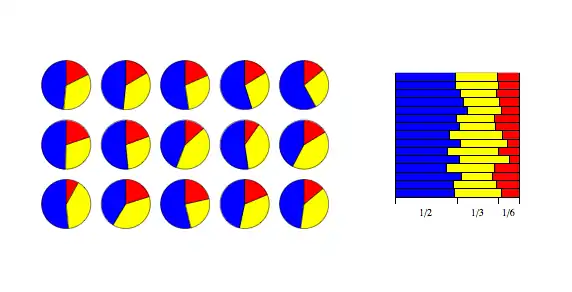
Découpage d'une ficelle
Une illustration de la distribution de Dirichlet apparaît lorsque l'on désire découper des ficelles (toutes de longueur initiale 1.0) en K pièces de différentes longueurs, et où chaque pièce a, en moyenne, une longueur désignée mais cette longueur est autorisée à varier. Les valeurs α/α0 spécifient les longueurs moyennes des découpes résultant de la distribution. La variance (disparité autour de la moyenne) varie inversement avec α0.
Modèles d'urne et simulations du cas particulier des urnes de Pólya
Considérons une urne contenant K couleurs différentes. Initialement, l'urne contient α1 boules de couleur 1, α2 boules de couleur 2, etc. Procédons alors à N tirages dans l'urne suivant ce protocole : chaque boule tirée est replacée dans l'urne et on y ajoute une boule supplémentaire de même couleur. Lorsque N devient très grand, les proportions des boules de différentes couleurs sont distribuées selon [1].
Notons que chaque tirage modifie la probabilité d'obtenir une couleur donnée. Cette modification s'atténue d'ailleurs avec le nombre de tirages, puisque l'effet marginal de l'ajout d'une boule supplémentaire diminue avec l'augmentation du nombre total de boules dans l'urne.
Références
- D. Blackwell and J. B. MacQueen 1973. Ferguson distributions via Pólya urn schemes. The Annals of Statistics, volume 1, number 2, pp353--355
Voir aussi
Articles connexes
Liens externes
Non-Uniform Random Variate Generation, par Luc Devroye http://cg.scs.carleton.ca/~luc/rnbookindex.html
- SciencesPo: Un package de R qui contient des fonctions pour simuler des paramètres d'une distribution de Dirichlet.






![\mathrm{E}[X_i] = \frac{\alpha_i}{\alpha_0},](https://img.franco.wiki/i/6913b45effc05651db14725c8d1664ed1e611d7b.svg)
![\mathrm{Var}[X_i] = \frac{\alpha_i (\alpha_0-\alpha_i)}{\alpha_0^2 (\alpha_0+1)},](https://img.franco.wiki/i/999314674c510668913c93c961ce9cf2552b8f89.svg)

![\mathrm{Cov}[X_iX_j] = -\frac{\alpha_i \alpha_j}{\alpha_0^2 (\alpha_0+1)}.](https://img.franco.wiki/i/43b147251bdf8cc83f899877197895f42b8a852e.svg)
















