Hexadécagone
Un hexadécagone (parfois appelé hexakaidécagone) est un polygone à 16 sommets, donc 16 côtés et 104 diagonales.
La somme des angles internes d'un hexadécagone non croisé vaut 2 520 degrés.
Nom
Le nom du polygone est formé à partir des préfixes hexa et déca. Hexa provient du grec ancien ἕξ (hex, six) et déca de δέκα (deca, dix). En grec ancien, seize se dit έκκαίδεκα (ekkaideka).
Hexadécagone régulier
Un hexadécagone régulier est un hexadécagone dont les seize côtés ont la même longueur et dont les angles internes ont même mesure. Il y en a quatre : trois étoilés (les hexadécagrammes notés {16/3}, {16/5} et {16/7}) et un convexe (noté {16}). C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'hexadécagone régulier ».
- Les trois hexadécagones réguliers étoilés
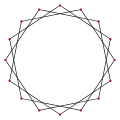 {16/3} (angle interne : 112,5°)
{16/3} (angle interne : 112,5°)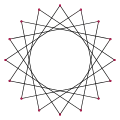 {16/5} (angle interne : 67,5°)
{16/5} (angle interne : 67,5°)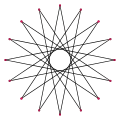 {16/7} (angle interne : 22,5°)
{16/7} (angle interne : 22,5°)
Dimensions
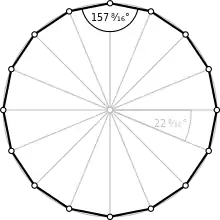
Chaque angle interne de l'hexadécagone régulier mesure et chaque angle au centre, .
Si chaque côté de l'hexadécagone mesure a :
- son rayon (c'est-à-dire le rayon de son cercle circonscrit) mesure
- ;
- son apothème (c'est-à-dire le rayon de son cercle inscrit) mesure
- ;
- son aire mesure
- ;
- son périmètre mesure .
Propriétés
16 étant une puissance de 2, l'hexadécagone régulier est, d'après le théorème de Gauss-Wantzel, constructible à la règle et au compas.
Son groupe de symétrie est le groupe diédral D16. Son symbole de Schläfli est {16}.
Voir aussi
(en) Eric W. Weisstein, « Hexadecagon », sur MathWorld





